来点斜率优化？

目录

• 前置芝士
• 原理介绍
• [ZJOI2007]仓库建设
• P2365 任务安排
• P3628 [APIO2010]特别行动队
• #10191. 「一本通 5.6 练习 4」打印文章
  • 有个坑点
• P4360 [CEOI2004]锯木厂选址
• CF311B Cats Transport
• P5504 [JSOI2011] 柠檬

前置芝士

• 单调队列
• 会写方程
• 初中数学基础
• 斜率优化原理

大多数斜率优化真的都是套路
学之前以为比较难，会用之后发现主要的难点还是在转移方程，这种优化啥的，就推推式子，然后结合单调队列，优化复杂度

建议大家回了思想以后还是要多自己手推一下，化两个式子就差不多了
至于一开始的DP方程，就看经验和造化了

原理介绍

本来就打算只写题，所以这部分内容先咕咕了

[ZJOI2007]仓库建设

我们设 \(f_i\) 表示在 \(i\) 处建立工厂所需的最小花费，显然要枚举一个上一次建厂的位置 \(j\)，根据题意很容易得出转移方程

\[\large f_i = \min \{ f_j + \sum_{k = j + 1}^{i} P_k(x_i - x_k) \} \]

其中 \(P_x\) 表示 \(x\) 处的物品数，\(x_i\) 表示 \(i\) 点到一号点的距离

对这个式子进行化简

\[\large f_i = \min \{ f_j + x_i \sum_{k = j + 1}^{i} P_k - \sum_{k = j + 1}^{i} P_k x_k \} \]

发现两个求和式子都可以用前缀和预处理，所以设 \(sum_x = \sum_{i = 1}^{x} P_i\)， \(val_x = \sum_{i = 1}^{x} P_ix_i\)，得

\[\large f_i = f_j + x_i (sum_i - sum_j) - (val_i - val_j) + cost_i \]

设 \(j\) 比 \(k\) 优，那么

\[\large f_j - x_i sum_j + val_j \le f_k - x_i sum_k + val_k \]

\[\large x_i (sum_k - sum_j) \le (f_k + val_k) - (f_j + val_j) \]

设 \(F_x = f_x + val_x\)，则

\[\large x_i (sum_k - sum_j) \le F_k - F_j \]

\[\large x_i \le \frac{F_k - F_j}{sum_k - sum_j} \]

所以说只要 $ \large x_i > \frac{F_k - F_j}{sum_k - sum_j}$ 单调队列中所维护的答案就不合法，将不合法元素从队首弹出即可

维护一个单调递增队列即可

设 \(K(x_1, x_2) = \frac{F_{x_1} - F_{x_2}}{sum_{x_1} - sum_{x_2}}\)

那么不合法条件是 \(K(q_{tail - 1}, q_{tail}) > K(q_{tail - 1}, pos)\)，（\(pos\) 是新加入的点）

代码也非常好写

/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define LL long long
#define int long long
#define orz cout<<"lkp AK IOI!"<<endl

using namespace std;
const int MAXN = 1e6+5;
const int INF = 1e9+7;
const int mod = 1e9+7;

int n;
int dis[MAXN], a[MAXN], cost[MAXN];
int sum[MAXN], val[MAXN];
int f[MAXN];
int q[MAXN], head = 1, tail = 0;

int read(){
    int s = 0, f = 0;
    char ch = getchar();
    while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
    while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
    return f ? -s : s;
}

int F(int x) { return f[x] + val[x]; }

double K(int x_1, int x_2) {
    if(sum[x_1] == sum[x_2]) return F(x_1) > F(x_2) ? 1e9 : -1e9;
    return (F(x_1) - F(x_2)) / (sum[x_1] - sum[x_2]);
}

void Delete(int pos){ while(head < tail && dis[pos] > K(q[head], q[head + 1])) head ++; }

void Insert(int pos) {
    while(head < tail && K(q[tail - 1], q[tail]) > K(q[tail - 1], pos)) tail --;
    q[++ tail] = pos;
}
signed main()
{
    n = read();
    for(int i = 1; i <= n; ++i) dis[i] = read(), a[i] = read(), cost[i] = read();
    for(int i = 1; i <= n; ++i) {
        sum[i] = sum[i - 1] + a[i];
        val[i] = val[i - 1] + a[i] * dis[i];
    }
    Insert(0);
    for(int i = 1; i <= n; ++i) {
        Delete(i);
        int j = q[head];
        f[i] = f[j] + dis[i] * (sum[i] - sum[j]) - val[i] + val[j] + cost[i];
        Insert(i);
    }
    printf("%lld", f[n]);
    return 0;
}

P2365 任务安排

Description

题面：P2365 任务安排

Solution

设 \(f_i\) 表示到第 \(i\) 个任务所需的最少花费，则有转移方程
有一说一我切完这道题才读懂了题面

\[f_i = f_j + t_i(c_i - c_j) + S(c_n - c_j) \]

其中 \(t_i\) 表示所需时间的前缀和， \(c_i\) 表示费用系数的前缀和

同样是设 \(j\) 比 \(k\) 优，则

\[f_j + t_i(c_i - c_j) + S(c_n - c_j) \le f_k + t_i(c_i - c_k) + S(c_n - c_k) \]

整理得

\[t_ic_k - t_ic_j \le (f_k - Sc_k) - (f_j - Sc_j) \]

设 \(F(x) = f_x - Sc_x\)，那么

\[t_i \le \frac{F(k) - F(j)}{c_k - c_j} \]

然后就和上面一个套路了

Code

/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define LL long long
#define int long long
#define orz cout<<"lkp AK IOI!"<<endl

using namespace std;
const int MAXN = 3e5+5;
const int INF = 1e9+7;
const int mod = 1e9+7;

int n, S;
int tim[MAXN], cost[MAXN];
int t[MAXN], c[MAXN];
int f[MAXN];
int q[MAXN], head = 1, tail = 0;

int read(){
    int s = 0, f = 0;
    char ch = getchar();
    while(!isdigit(ch))  f |= (ch == '-'), ch = getchar();
    while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
    return f ? -s : s;
}

double F(int x) {
    return f[x] - S * c[x];
}

double K(int x_1, int x_2) {
//    if(c[x_2] == c[x_1]) return F(x_1) > F(x_2) ? 1e9 : -1e9;
    return (double)(F(x_2) - F(x_1)) / (c[x_2] - c[x_1]);
}

void Delete(int pos) {
//    cout<<pos<<" "<<t[pos]<<" "<<K(q[head], q[head + 1])<<endl;
    while(head < tail && t[pos] > K(q[head], q[head + 1])) head ++;
}

void Insert(int pos) {
    while(head < tail && K(q[tail], q[tail - 1]) > K(q[tail - 1], pos)) tail --;
    q[++ tail] = pos;
}

signed main()
{
    n = read(), S = read();
    for(int i = 1; i <= n; ++i) {
        tim[i] = read(), cost[i] = read();
        t[i] = t[i - 1] + tim[i], c[i] = c[i - 1] + cost[i];
    }
    Insert(0);
    for(int i = 1; i <= n; ++i) {
        Delete(i);
        int j = q[head];
        f[i] = f[j] + t[i] * (c[i] - c[j]) + S * (c[n] - c[j]);
        Insert(i);
    }
    printf("%lld", f[n]);
    return 0;
}

P3628 [APIO2010]特别行动队

Description

题面：P3628 [APIO2010]特别行动队

Solution

设 \(f_i\) 表示到第 \(i\) 个士兵所得到的最大战斗力，易得转移方程

\[\large f_i = f_j + a(sum_i - sum_j)^2 + b(sum_i - sum_j) + c \]

其中 \(sum_i\) 表示前 \(i\) 个士兵的战斗力之和

让我们再次假设 \(j\) 比 \(k\) 优，那么

\[f_j + a(sum_i - sum_j)^2 + b(sum_i - sum_j) + c \ge f_k + a(sum_i - sum_k)^2 + b(sum_i - sum_k) + c \]

化简得

\[2 \times a \times sum_i \ge \frac{(f_k + a \times sum_k^2) - (f_j + a \times sum_j^2)}{sum_k - sum_j} \]

设 \(F(x) = f_x + a \times sum_x^2 - b \times sum_x\)

\[\large 2 \times a \times sum_i \ge \frac{F(k) - F(j)}{sum_{k} - sum_{j}} \]

发现 \(a\) 是负数，所以就不移到右边了
然后就是板子了，一个套路
话说要是除过去一个负数咋整啊，不用变号？

Code

/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define LL long long
#define int long long
#define orz cout<<"lkp AK IOI!"<<endl

using namespace std;
const int MAXN = 1e6+5;
const int INF = 1e9+7;
const int mod = 1e9+7;

int n, a, b, c;
int sum[MAXN], f[MAXN];
int q[MAXN], head = 1, tail = 0;

int read(){
    int s = 0, f = 0;
    char ch = getchar();
    while(!isdigit(ch))  f |= (ch == '-'), ch = getchar();
    while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
    return f ? -s : s;
}

int F(int x) { return f[x] + a * sum[x] * sum[x] - b * sum[x]; }
double K(int x_1, int x_2) { return (F(x_1) - F(x_2)) / ((sum[x_1] - sum[x_2])); }
void Delete(int pos) { while(head < tail && 2 * sum[pos] * a < K(q[head], q[head + 1])) head ++; }
void Insert(int pos) {
    while(head < tail && K(q[tail - 1], q[tail]) < K(q[tail - 1], pos)) tail --;
    q[++ tail] = pos;
}

signed main()
{
    n = read(), a = read(), b = read(), c = read();
    for(int i = 1; i <= n; ++i) sum[i] = sum[i - 1] + read();
    Insert(0);
    for(int i = 1; i <= n; ++i) {
        Delete(i);
        int j = q[head], sum_ = sum[i] - sum[j];
        f[i] = f[j] + a * sum_ * sum_ + b * sum_ + c;
        Insert(i);
    }
    printf("%lld", f[n]);
    return 0;
}

#10191. 「一本通 5.6 练习 4」打印文章

Description

题面：#10191. 「一本通 5.6 练习 4」打印文章

Solution

设 \(f_i\) 表示前 \(i\) 个数的最小花费，根据题意可得转移方程

\[\large f_i = \min \{ f_j + (\sum_{k = j + 1}^{i} c_k)^2 + M \} \]

维护一个前缀和

\[\large f_i = \min \{ f_j + (sum_i - sum_j)^2 + M \} \]

设 \(j\) 比 \(k\) 优，则

\[\large f_j + (sum_i - sum_j)^2 + M \le f_k + (sum_i - sum_k)^2 + M \]

进行化简，将与 \(i\) 有关的项移到左边，剩下的移到右边

设 \(F(x) = f_x + sum_x^2\) 得

\[2sum_i \le \frac{F(k) - F(j)}{sum_k - sum_j} \]

进行斜率优化即可

有个坑点

来看一眼这个数据

5 2
9
0
5
6
9

中间有个 \(0\)， 那么 \(sum_1 = sum_2 = 9\)

如果此时进行除法运算，因为分子相减可能为 0，所以计算机会运行出错，会返回一个极大值，但极大值不能显示，只能返回一个 nan 字样

这时可以将它转化成整形，它就会因为自然溢出而变成一个极小值，可能恰好对答案是对的

另外一种处理方式是判断分子是否为 0，然后比较分母的大小，通过判断返回一个极大值或者极小值

Emm……，
经过测试，对于上面这组样例返回极大值和极小值一个样，判断的符号是大于还是小于都不影响答案

如果有大佬遇到返回极大值或极小值，或者大于号小于号对答案有影响的时候，望指出

Code

/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define LL long long
#define int long long
#define orz cout<<"lkp AK IOI!"<<endl

using namespace std;
const int MAXN = 5e5+5;
const int INF = 1e9+7;
const int mod = 1e9+7;

int n, m;
int sum[MAXN], f[MAXN];
int q[MAXN], head = 1, tail = 0;

int read(){
    int s = 0, f = 0;
    char ch = getchar();
    while(!isdigit(ch))  f |= (ch == '-'), ch = getchar();
    while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
    return f ? -s : s;
}

LL F(int x) { return f[x] + sum[x] * sum[x]; }
double K(int x_1, int x_2) { 
    if(sum[x_1] == sum[x_2]) return F(x_1) > F(x_2) ? 1e9 : -1e9;
    return (double)(F(x_1) - F(x_2)) / (sum[x_1] - sum[x_2]); 
}
// 或者这个
// LL K(int x_1, int x_2) { 
//    return (double)(F(x_1) - F(x_2)) / (sum[x_1] - sum[x_2]); 
//}
void Delete(int pos) { 
    while(head < tail && 2 * sum[pos] > K(q[head + 1], q[head])) head ++; 
}
void Insert(int pos) {
    while(head < tail && K(q[tail], q[tail - 1]) > K(pos, q[tail])) tail --;
    q[++ tail] = pos;
}

signed main()
{
    while(cin >> n >> m) { 
        for(int i = 1; i <= n; ++i) sum[i] = sum[i - 1] + read();
        Insert(0);
        for(int i = 1; i <= n; ++i) {
            Delete(i);
            int j = q[head], sum_ = sum[i] - sum[j];
            f[i] = f[j] + sum_ * sum_ + m;
            Insert(i);
        }
        printf("%d\n", f[n]);
        memset(sum, 0, sizeof sum);
        memset(f, 0, sizeof f);
        head = 1, tail = 0;
    }
    return 0;
}

P4360 [CEOI2004]锯木厂选址

Description

P4360 [CEOI2004]锯木厂选址

Solution

状态设计可能不好想，考虑在哪里建两个厂更省钱

设 \(f_i\) 表示将第二个建在 \(i\) 处， 第一个建在 \(j\) 处（\(j < i\)）后最多省的钱

\[\large f_i = sum_i \times dis_i + sum_j \times (dis_j - dis_i) \]

其中 \(dis_x = \sum_{i = x}^{n} d_i,sum_x = \sum_{i = 1}^{x}w_i, val_x = \sum_{i = 1}^{x} w_i \times dis_i\)

设 \(j\) 比 \(k\) 优，

\[sum_i \times dis_i + sum_j \times (dis_j - dis_i) \ge sum_i \times dis_i + sum_k \times (dis_k - dis_i)\]

设 \(F(x) = s_xd_x\) 化简得

\[d_i \ge \frac{F(k) - F(j)}{s_k - s_j} \]

都不建的花费为

\[\sum_{i = 1}^{n} w_i \times dis_i \]

所以都不建的花费可以表示为 \(val_n\)

最后的答案为 \(val_n - \max_{1 \le i \le n} \{f_i \}\)

Code

/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define LL long long
#define int long long
#define orz cout<<"lkp AK IOI!"<<endl

using namespace std;
const int MAXN = 2e5+5;
const int INF = 1e9+7;
const int mod = 1e9+7;

int n, ans = 0;
int w[MAXN], d[MAXN];
int sum[MAXN], val[MAXN];
int f[MAXN];
int q[MAXN], head = 1, tail = 0; 

int read(){
    int s = 0, f = 0;
    char ch = getchar();
    while(!isdigit(ch))  f |= (ch == '-'), ch = getchar();
    while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
    return f ? -s : s;
}

int F(int x) { return sum[x] * d[x] - sum[x] * d[n + 1]; }
double K(int x_1, int x_2) {
    if(sum[x_1] == sum[x_2]) return F(x_1) > F(x_2) ? 1e9 : -1e9;
    return (double)((F(x_1) - F(x_2)) / (sum[x_1] - sum[x_2])); 
}
void Delete(int pos) { while(head < tail && d[pos] < K(q[head], q[head + 1])) head ++; }
void Insert(int pos) {
    while(head < tail && K(q[tail], q[tail - 1]) < K(q[tail], pos)) tail --;
    q[++ tail] = pos;
}

signed main()
{
    n = read();
    for(int i = 1; i <= n; ++i) w[i] = read(), d[i] = read();
    for(int i = n; i >= 1; --i) d[i] += d[i + 1];
    for(int i = 1; i <= n + 1; ++i) sum[i] = sum[i - 1] + w[i], val[i] = val[i - 1] + w[i] * d[i];
    Insert(0);
    for(int i = 1; i <= n; ++i) {
        Delete(i);
        int j = q[head];
        f[i] = sum[i] * d[i] + sum[j] * (d[j] - d[i]);
        Insert(i);
    }
    for(int i = 1; i <= n; ++i) ans = max(ans, f[i]);
    printf("%lld", val[n] - ans);
    return 0;
}

CF311B Cats Transport

Description

题面：CF311B Cats Transport

Solution

好题哇好题！

一开始拿到这题，那是半点思路也没有（wtcl

知道我从讨论中翻到了以为大佬的这张图：

不得不说，这张图给了我启发

饲养员的路径是一条形似 \(y = x + b\) 的直线
而每只猫可以看做一个点，横坐标是它到 \(1\) 号山的距离，总左边是它玩完的时间

假设一个饲养员可以恰好接走这只猫，根据初中的一次函数代入点的坐标解出 \(b\) 的值（即饲养员恰好接走这只猫的出发时间），先将其存到 \(cat\) 数组中

再来看一下下面这张图，其中 \(A - F\) 均代表一只猫， \(H, I\) 分别是 \(E, F\) 两个点所在的直线与 \(y\) 轴的交点

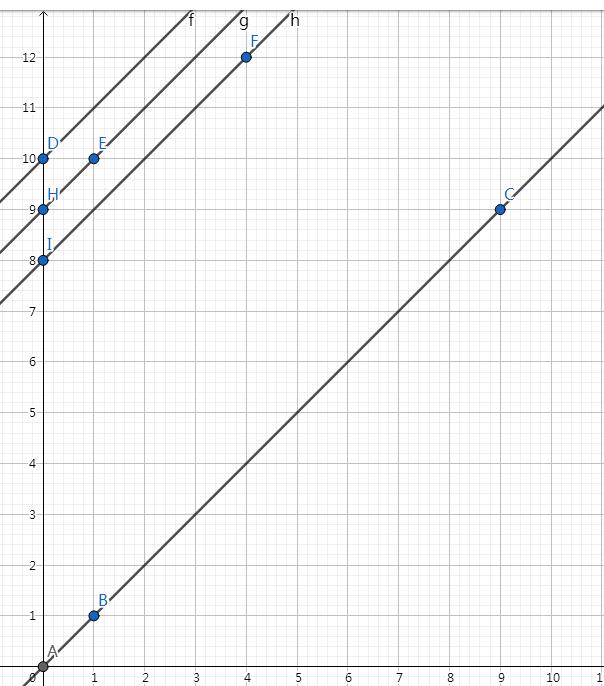
不难发现，假设一个饲养员能够接走 \(D, E, F\)，那么他最优时是从 \(10\) 出发，也就是 \(cat_D\)，那么 \(E, F\) 两只猫等待的时间分别为 \(cat_D - cat_E, cat_D - cat_F\) 。

\(cat\) 数组不是递增的要先排个序

看起来有点眉目，让我们先yy个转移方程，因为只有 \(p\) 个饲养员，再加一维表示轮到第几个饲养员即可

设 \(f_{i, j}\) 为恰好接到第 \(j\) 只猫用 \(i\) 个人时所用的最小等待时间，其中 \(q\) 表示上一只恰好接到的猫为第 \(q\) 只。

\[f_{i, j} = f_{i - 1, q} + \sum_{k = q + 1}^{j} cat_j - cat_k \]

\[f_{i, j} = f_{i - 1, q} + (j - q) cat_j - \sum_{k = q + 1}^{j} cat_k \]

其中 \(t_i\) 表示第 \(i\) 只猫玩完的时间， \(sum_i\) 表示第 \(i\) 只猫到 \(1\) 号山的距离

设 \(val_x = \sum_{i = 1}^{x} (t_i - sum_i)\)，所以

\[f_{i, j} = f_{i - 1, q} + (j - q)cat_j + val_j - val_p \]

假设 \(q\) 比 \(k\) 优

\[f_{i - 1, q} + (j - q)cat_j - val_j + val_q \le f_{i - 1, k} + (j - k)cat_j - val_j + val_k \]

化简得

\[cat_j \le \frac{(f_{i - 1, k} - val_k) - (f_{i - 1, q} - val_q)}{k - q} \]

设 \(F(x) = f_{i - 1, x} - val_x\)，则

\[cat_j \le \frac{F(k) - F(q)}{k - q} \]

然后进行斜率优化即可

Code

/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define LL long long
#define int long long
#define orz cout<<"lkp AK IOI!"<<endl

using namespace std;
const int MAXN = 1e5+5;
const int INF = 1e9+7;
const int mod = 1e9+7;

int n, m, p;
int sum[MAXN], val[MAXN], cat[MAXN];
int f[105][MAXN];
int q[MAXN], head = 1, tail = 0;

int read(){
    int s = 0, f = 0;
    char ch = getchar();
    while(!isdigit(ch))  f |= (ch == '-'), ch = getchar();
    while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
    return f ? -s : s;
}

int F(int i, int x) { return f[i - 1][x] + val[x]; }
double K(int i, int x_1, int x_2) { return 1.0 * (F(i, x_1) - F(i, x_2)) / (x_1 - x_2); }
void Delete(int i, int pos) { while(head < tail && cat[pos] > K(i, q[head], q[head + 1])) head ++; }
void Insert(int i, int pos) {
    while(head < tail && K(i, q[tail], q[tail - 1]) > K(i, q[tail], pos)) tail --;
    q[++ tail] = pos;
}

signed main()
{
    n = read(), m = read(), p = read();
    for(int i = 2; i <= n; ++i) sum[i] = sum[i - 1] + read();
    for(int i = 1, H, T; i <= m; ++i) {
        H = read(), T = read();
        cat[i] = T - sum[H];
    }
    sort(cat + 1, cat + m + 1);
    for(int i = 1; i <= m; ++i) val[i] = val[i - 1] + cat[i];
    for(int i = 1; i <= m; ++i) f[1][i] = i * cat[i] - val[i];
    for(int i = 2; i <= p; ++i) {
        head = 1, tail = 0;
        for(int j = 0; j < i; ++j) Insert(i, j);
        for(int j = i; j <= m; ++j) {
            Delete(i, j);
            int now_ = q[head];
            f[i][j] = f[i - 1][now_] + (j - now_) * cat[j] - val[j] + val[now_];
            Insert(i, j);
        }
    }
    printf("%lld", f[p][m]);
    return 0;
}

P5504 [JSOI2011] 柠檬

Description

题面：P5504 [JSOI2011] 柠檬

Solution

暂咕

Code

/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<vector>
#define LL long long
#define int long long
#define orz cout<<"lkp AK IOI!"<<endl

using namespace std;
const int MAXN = 2e5+5;
const int INF = 1e9+7;
const int mod = 1e9+7;

int n;
int a[MAXN], sum[MAXN], head[MAXN];
vector<int> stc[20010];
int f[MAXN];

int read(){
    int s = 0, f = 0;
    char ch = getchar();
    while(!isdigit(ch))  f |= (ch == '-'), ch = getchar();
    while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
    return f ? -s : s;
}

int X(int pre_) { return 2 * a[pre_] * sum[pre_]; }
int F(int pre_) { return f[pre_ - 1] + a[pre_] * sum[pre_] * sum[pre_]; }
double K(int x_1, int x_2) { return (double)((F(x_1) - F(x_2)) / (X(x_1) - X(x_2))); }

void Delete(int pos) {
    int siz_ = a[pos], top = stc[siz_].size();
    while(top > 1 && K(stc[siz_][top - 1], stc[siz_][top - 2]) < sum[pos] + 1) stc[siz_].pop_back(), top --;
}

void Insert(int pos) {
    int siz_ = a[pos], top = stc[siz_].size();
    while(top > 1 && K(stc[siz_][top - 1], stc[siz_][top - 2]) < K(stc[siz_][top - 1], pos)) stc[siz_].pop_back(), top --;
    stc[siz_].push_back(pos);
}

signed main()
{
    n = read();
    for(int i = 1; i <= n; ++i) {
        a[i] = read();
        sum[i] = sum[head[a[i]]] + 1;
        head[a[i]] = i;
    }
//    for(int i = 1; i <= n; ++i) cout<<sum[i]<<" ";
//    cout<<"\n";
    for(int i = 1; i <= n; ++i) {
        Insert(i);
        Delete(i);
        int j = stc[a[i]][stc[a[i]].size() - 1], sum_ = sum[i] - sum[j] + 1;
//        cout<<j<<" "<<sum_<<" ";
        f[i] = f[j - 1] + a[i] * sum_ * sum_;
//        cout<<f[i]<<" \n";
    }
    printf("%lld", f[n]);
    return 0;
}