21210228 DP专题
前言
考前龙这样说:
“这次出的简单点,主要是图论&DP”
然后他不知道从哪搬的题,貌似是清北的一次Day3,三个题全DP给我干蒙了/kk
预计得分:\(?pts + 30pts + ?pts = 30pts\)
实际得分:\(5pts + 30pts + 0pts = 35pts\)
T1和T3 yy了两个贪心,然后贪假了/wul
T1 \(5pts\) 是样例/kk
Update 2021/02/28 : 贪心是对的,然后T3是因为 get 是个关键字编译失败,改成驼峰后有 \(70pts\)
正文
T1
Description
给定 \(n\) 个汉字和每个汉字 \(a_i\) 出现的次数。要求用
a和ha对其进行加密处理,每个汉字加密后的字符串是独一无二的(即不能出现一个是另一个前缀的形式),求加密后文章长度最短是多少
\(3 \le n \le 750, 1 \le a_i \le 1e5\)
Solution
我们可以想到其实这道题是棵树!:
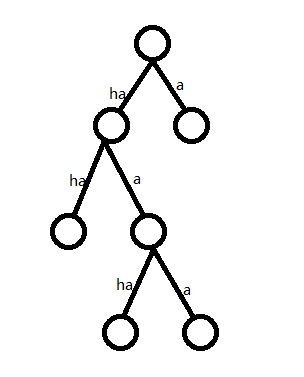
因为不能存在前缀,所以我们只能选这棵树上的叶子结点
那么问题转化成在这棵很神仙的树上面选择 \(n\) 个没有祖先后代关系(实际上就是叶子结点)的结点所需要的最少层数(我们把 ha 看做两层, a 看做一层)
显然出现次数多的应该放在层数少的地方,所以排序预处理
显然任意一棵有 \(n\) 个叶子结点的树都是一种方案,我们的目的是找一个最小的
那么我们从 \(n\) 开始枚举
首先我们设 \(\large f_{i,x,y,k}\) 表示当前到了第 \(i\) 层,这一层 \(x\) 个结点(这个结点是作为叶子还是继续生长我们不确定),
第 \(i + 1\) 层 \(y\) 个结点,已经有 \(k\) 个确定了
让我们枚举一个 \(p\) ,表示将 \(i\) 这一层中的 \(p\) 个结点设为叶子,剩下的向下扩展,那么
其中 \(sum_{i}\) 表示排序后前 \(i\) 个汉字的数量和
对呀为什么 \(sum_n - sum_{k +p}\) 放在右边而不是左边
我们来解释一下上面的式子:
- 这一层有 \(p\) 个被置为叶子不能再生长了。那么剩下的 \(x - p\) 个结点,既可以向下一层扩展 \(x - p\) 个结点,也可以向下两层扩展 \(x - p\) 个结点
所以对于第 \(i + 1\) 层,这一层有 \(y + x - p\) 个结点,下一层有 \(x - p\) 个结点,前 \(i\) 层用过的节点为 \(k + p\) 个,同时剩下的 \(n - k - p\) 个汉字至少要放在第 \(i + 1\) 层的位置,因此要统计他们造成的贡献
复杂度为 \(O(n^5)\)
考虑降维,发现 \(i\) 只和 第 \(i + 1\) 层相关,改为倒序枚举即可直接把第一维压掉
转移方程不变:
时间复杂度: \(O(n^4)\)
考虑优化转移:每次枚举一个 \(p\) 未免太浪费时间,我们可以考虑每次把其中的一个变成叶子,这样如果想达到枚举p的效果,只需要减去多次1即可,或者直接将所有的结点向下继续建树;
转移方程改为:
前一半不知道还剩下多少个汉字,所以暂时先不统计贡献
后半部分的理解和上面同理:这一层的 \(x\) 个结点直接向下扩展,所以下一层和下两层分别加 \(x\) 的节点
时间复杂度: \(O(n^3)\)
发现最后一维对答案貌似没啥影响,所以std就没写?,考虑压掉,只用三维(加上滚动数组)
加上滚动数组优化,时间复杂度 \(O(n^2)\)
zhhx 题解原话:
- 首先我们设 $dp[i][x][y][k]$ 表示当前到了第 $i$ 层,这一层 $x$ 个,
上一层 $y$ 个,已经有 $k$ 个结束了
- 转移的话就直接枚举一下,$y$ 这一层有 $p$ 个结束了即可,然
后算上结束的代价
- Time complexity $O(N^5)$ 到 $O(N^4 ∗ log(N))$
我们考虑把第一维优化掉,我们设 $dp[x][y][k]$ 表示最下方一
层 $x$ 个,倒数第二层 $y$ 个,结束了 $k$ 个。
- 转移的时候就直接,枚举 $y$ 这一层结束了 $p$ 个,注意这里代
价不是每一个元素结束的时候记上了,我们在没往下一层
时,我们算一下这一层会产生的贡献。
- Time complexity O(N^4)
我们再把转移优化掉。
- 我们就考虑每一次是把 $y$ 减 $1$ 表示,把倒数第二层一个元
素封上,还是把 $y$ 个全部分叉转移到 $dp[y][x+y][k]$,加上这
一层的贡献即可。
- Time complexity O(N^3) 滚动数组优化后 Space complexity
O(N^2)
Code
激动人心的代码环节/se
/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 777;
const int INF = 1e9+7;
const int mod = 1e9+7;
int n, a[MAXN], sum[MAXN];
int f[2][MAXN][MAXN];
int r;
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
bool cmp(int x, int y) { return x > y; }
int main()
{
freopen("A.in","r",stdin);
freopen("A.out","w",stdout);
n = read();
for(int i = 1; i <= n; ++i) a[i] = read();
sort(a + 1, a + n + 1, cmp);//排序
for(int i = 1; i <= n; ++i) sum[i] = sum[i - 1] + a[i];//前缀和
for(int i = 0; i < MAXN; ++i)
for(int j = 0; j < MAXN; ++j)
f[0][i][j] = f[1][i][j] = INF;//初始化
r = 0;
f[r][0][0] = 0;//滚动数组优化
for(int k = n - 1; k >= 0; --k) { //已经完成了k个
for(int y = n - k; y >= 0; --y) { //下一层y个
for(int x = n - k - y; x >= 0; --x) { //这一层x个
f[r ^ 1][x][y] =
min(INF, (!x && !y) ? INF :
min( !y ? INF : f[r][x][y - 1], x + y + y + k > n ? INF : f[r ^ 1][y][x + y] + sum[n] - sum[k])
);//zhhx三个三目运算符套起来太恶心了
}
}
r ^= 1;
}
printf("%d", sum[n] + f[r][1][1]);
return 0;
}
T2
Description
给定一个区间 \([L,R]\) 和一个表示进制的 \(C\),求 \([L,R]\) 中有多少个数字是优美的。一个数字优美的定义是,原数能被 \(C\) 进制下该数各个数位的和 整数
\(1 \le L \le R \le 10^{18}, 2 \le C \le 15\)
Solution
简直是洛谷同余分布的强化版,加了个进制限制而已,某人早已写过题解此题却爆零蛤蛤
正解其实和它那做法差不多,如果有进制限制,就按进制限制来拆位即可
题解代码就那意思,反正我没看明白
Code
/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 1e5+5;
const int INF = 1e9+7;
LL R, L;
int C;
int a[70], numa, b[70], numb, p[70];
int mod;
LL f[70][400][400];
LL read(){
LL s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
LL Query(int *a, int i, int sum, int rest, bool flag) {
// 对应数、还剩几位、剩下i位的和、余数、
if(sum < 0) return 0;
if(i == 0) return !sum && !rest ? 1 : 0;
if(!flag && f[i][sum][rest] != -1) return f[i][sum][rest];
LL ans = 0;
int up = flag ? a[i] : C - 1;
for(int j = 0; j <= up; ++j) {
ans += Query(a, i - 1, sum - j, (rest + mod - j * p[i] % mod) % mod, flag && j == up);
}
if(!flag) f[i][sum][rest] = ans;
return ans;
}
int main()
{
freopen("B.in","r",stdin);
freopen("B.out","w",stdout);
L = read(), R = read(), C = read();
L--;
while(R) a[++numa] = R % C, R /= C;
while(L) b[++numb] = L % C, L /= C;
memset(f, -1, sizeof f);
LL ans = 0;
for(int i = 1; i <= numa * C; ++i) {
mod = i;
p[1] = 1;
for(int j = 2; j <= numa; ++j) p[j] = p[j - 1] * C % mod;
ans += Query(a, numa, mod, 0, true) - (numb == 0 ? 0 : Query(b, numb, mod, 0, true));
for(int x = 0; x <= numa; ++x)
for(int y = 0; y <= i; ++y)
for(int z = 0; z <= mod; ++z)
f[x][y][z] = -1;
}
cout<<ans;
return 0;
}
T3
Description
给定 \(n\) 个线段和一个整数 \(k\),以及每条线段的左右端点 \(L, R\)。表示将这 \(n\) 个线段分为 \(k\) 组,使其总价值最大。每组价值的计算方法是每组中线段的交的长度,总价值是每组价值的和。
\(1 \le k \le n \le 6000, 1 \le L_i < R_i \le 10^6\)
\(70pts\) 贪心
Solution
考场乱搞,因为有 get 关键字而 CE,悲
考虑每次只合并两条线段
先 \(n^2\) 处理出每两条线段合并所损失的线段长度 \(cut\),并将其和两线段编号塞入优先队列中
然后取出 \(cut\) 最小的,将对应的一对线段合并
每次新开一个优队,那么一共需要合并 \(n - k\) 次
-
\(cut\) 的计算方式:两线段总长减去两线段的交的长度
-
每次注意标记合并完的线段,并更新一个线段。暴力处理乱搞即可。
注意,\(a,b\) 两端点合并后的新线段的左端点为 \(\max \{L_a, L_b\}\) ,右端点为 \(\min \{R_a,R_b \}\),应该很显然
时间复杂度: \(O(n^2 (n + \log n))\)
Code
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<queue>
#define orz cout<<"lkp AK IOI\n"
using namespace std;
const int MAXN = 2e6+5;
const int INF = 1e9+7;
const int mod = 1e9+7;
int n, k, ans = 0, lose, Get;//大意了,get是个关键词,只好改成驼峰
int L[MAXN], R[MAXN], len[MAXN];
bool vis[MAXN];
struct node{
int cut, fir, sec;
bool operator < (const node &b) const { return cut > b.cut; }
};
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + (ch ^ 48), ch = getchar();
return f ? -s : s;
}
void work() {
priority_queue<node> q;
for(int i = 1; i < n; ++i) {
if(vis[i]) continue;
for(int j = i + 1; j <= n; ++j) {
if(vis[j]) continue;
int cut = abs(L[j] - L[i]) + abs(R[j] - R[i]) + min(R[j], R[i]) - max(L[j], L[i]);
if(min(R[j], R[i]) < max(L[j], L[i])) cut = R[i] - L[i] + R[j] - L[j];
q.push((node){cut, i, j});
}
}
lose = q.top().sec, Get = q.top().fir;
vis[lose] = true;
L[Get] = max(L[Get], L[lose]);
R[Get] = min(R[Get], R[lose]);
}
int main(){
freopen("C.in","r",stdin);
freopen("C.out","w",stdout);
n = read(), k = read();
for(int i = 1; i <= n; ++i){
L[i] = read(), R[i] = read();
}
for(int i = k + 1; i <= n; ++i) work();
for(int i = 1; i <= n; ++i) {
if(!vis[i] && R[i] >= L[i]) ans += R[i] - L[i];
}
printf("%d", ans);
return 0;
}
\(100pts\) 正解
Solution
分情况讨论:
-
如果存在空集:显然最多只有一个空集,此时将前 \(k-1\) 长的线段分成 \(k-1\) 组,剩下的分成 \(1\) 组统计答案
-
假设没有空集的话。我们再观察一个性质,对于一个完全可以包含另一个线段 \(B\) 的线段 \(A\),\(A\) 肯定是要和 \(B\) 在一个组的。放别的组,肯定不优。
对于第二种情况,我们就把所有不被任何其他线段包含的 \(B\) 线段集合拿出来。假设有 \(m\) 个。然后这样的一组线段排序之后就是左端点升序的同时右端点也升序了。(假设右端点不是升序的显然就又出现了被包含的线段)这样的话我们选出的每一个集合,就是连续的一段线段了。看上去就能 dp 了。
设 \(dp_{i,j}\) 表示前 \(i\) 个线段选了 \(j\) 个集合,首先我们要保证没有空集,那么有:
显然把 \(l_i\) 提出来就可以单调队列优化了
Code
/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 1e5+5;
const int INF = 1e9+7;
const int mod = 1e9+7;
struct node{
int L, R;
}a[MAXN], b[MAXN];
int n, m, k, len_n, r;
LL len[MAXN], ans, dp[2][MAXN];
int q[MAXN], head = 1, tail = 0;
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
bool cmp(node x, node y) { return x.R == y.R ? x.L > y.L : x.R < y.R; }
bool cmp2(int x, int y) { return x > y; }
int main()
{
freopen("C.in","r",stdin);
freopen("C.out","w",stdout);
n = read(), k = read();
for(int i = 1; i <= n; ++i) a[i].L = read(), a[i].R = read(), len[i] = a[i].R - a[i].L;
sort(len + 1, len + n + 1);
for(int i = n; i >= n - k + 2; --i) ans += len[i];//先假设存在空集,计算前k - 1个线段的总和
// for(int i = 0; i < k - 1; ++i) ans += len[n - i];
sort(a + 1, a + n + 1, cmp);
memset(len, 0, sizeof len);
int mx = 0; //出现的最大左端点
for(int i = 1; i <= n; ++i) { //处理一个线段包含另一个线段的情况
if(a[i].L > mx) { // 如果比以前的大
b[++m] = a[i]; // 加入新队列
mx = a[i].L; // 更新
} else {
len[++len_n] = a[i].R - a[i].L;
}
}
sort(len + 1, len + len_n + 1, cmp2);//从大到小
// sort(len+1,len+len_n+1,greater<LL>());
for(int i = 2; i <= len_n; ++i) len[i] += len[i - 1]; // 前缀和
sort(b + 1, b + m + 1, cmp);//按照右端点升序排序
r = 1;
for(int i = 1; i <= m; ++i) {
if(b[1].R <= b[i].L) dp[0][i] = -INF;
else dp[0][i] = b[1].R - b[i].L;
}
ans = max(ans, dp[0][m] + len[k - 1]);
for(int j = 2; j <= min(k, m); ++j, r ^= 1) {
head = tail = 1;
q[1] = 1; dp[r][1] = -INF;
for(int i = 2; i <= m; ++i) {
while(head <= tail && b[q[head] + 1].R <= b[i].L) head ++;
if(head <= tail) dp[r][i] = dp[r ^ 1][q[head]] + b[q[head] + 1].R - b[i].L;
else dp[r][i] = -INF;
while(head <= tail && dp[r ^ 1][i] + b[i + 1].R >= dp[r ^ 1][q[tail]] + b[q[tail] + 1].R) tail--;
q[++tail] = i;
}
ans = max(ans, dp[r][m] + len[k - j]);
}
printf("%lld\n", ans);
return 0;
}
/*
5 3
5 11
16 22
14 20
10 20
6 10
*/

 把做爆了的开学测试呜呜
把做爆了的开学测试呜呜

 浙公网安备 33010602011771号
浙公网安备 33010602011771号