算法总结篇---AC自动机
写在前面
鸣谢:
OiWiki
「笔记」AC 自动机---LuckyBlock
字符串四姐妹---KnightL
AC自动机讲解超详细---某不知名大佬
Q:AC自动机?是能自己AC题目的算法吗?(兴奋)
A:不不不,那叫自动AC机,通过打开答案文件输出答案的一种小手段,在比赛中使用还会有禁赛三年的奖励,而AC自动机是一个字符串匹配算法
AC自动机,全称\(Aho-Corasick\ automaton\),是一种用来处理字符串多模式匹配的算法
本人将尽可能详细的解释AC自动机的算法流程(其实大部分抄的Oiwiki,这是一个帮助我们共同理解的过程,毕竟作者也是个萌新。开始接受的过程可能比较困难,但多回顾几遍还是有助于理解的
算法流程
什么是自动机?(粘个链接,感性理解就好,不要过于执着)
引例:
给定 \(n\) 个模式串 \(s_i\) 和一个文本串 \(t\),求有多少个不同的模式串在文本串里出现过。
两个模式串不同当且仅当他们编号不同。
概述:
结合Trie的结构和KMP的思想建立,建立一个AC自动机主要通过两个步骤:
-
1、建立Trie树;
-
2、对Trie树上的所有结点构造失配指针
Trie树的构建(第一步)
这个Trie树就是普通的Trie树,该怎么建怎么建
解释一下Trie树结点的含义:表示某个模式串的前缀
后文也将称作状态。一个结点表示一个状态,Trie树的边就是状态的转移
形式化的说,对于若干个模式串 \(s_1,s_2,s_3···s_n\),将它们构建一个Trie树后的所有状态的集合记为 \(Q\)
失配指针(第二步)
AC 自动机利用一个 fail 指针来辅助多模式串的匹配。
状态 \(u\) 的 fail 指针指向另一个状态 \(v\) ,其中 \(v \in Q\) ,且 \(v\) 是 \(u\) 的最长后缀(即在若干个后缀状态中取最长的一个作为 fail 指针)。
注意和KMP的next指针的区别:
两者都是在失配的时候用于跳转的指针;
next指针求的是最长的border(最长的 相同的 前后缀),而fail指针指向所有模式串的前缀中匹配当前状态的最长后缀
因为 KMP 只对一个模式串做匹配,而 AC 自动机要对多个模式串做匹配。有可能 fail 指针指向的结点对应着另一个模式串,两者前缀不同。但是另一个模式串的一定是这个模式串到这里的一个后缀。
AC 自动机在做匹配时,同一位上可匹配多个模式串。
构建失配指针
(可以参考KMP中构建next指针的思想(
考虑更新 \(fail_u\),\(u\) 的父节点是 \(p\) , \(p\) 通过字符 \(c\) 的边指向 \(u\) ,即 \(tr[p,c] = u\) 。假设深度小于 \(u\) 的所有结点的 \(fail\) 指针均已求得。
如果 \(tr[fail_p,c]\) 存在:则让 \(fail_u\) 指向 \(tr[fail[p],c]\) 。相当于在 \(p\) 和 \(fail\) 后面加一个字符
c,分别对应 \(u\) 和 \(fail_u\) 。
如果 \(tr[fail_p,c]\) 不存在:那么我们继续找到 \(tr[fail_{fail_p},c],c]\) 。重复 \(1\) 的判断过程,一直跳 \(fail_u\) 指针指到根结点。
如果真的没有,就让 \(fail_u\) 指针指向根结点。
举个例子,对字符串 i, he, his, she, hers 组成的字典树构建 fail 指针:
给张图,其中黄色点表示当前结点 \(u\),绿色点表示已经 bfs 完成的点,橙边是 fail 指针,红边是当前求出的 fail 指针。
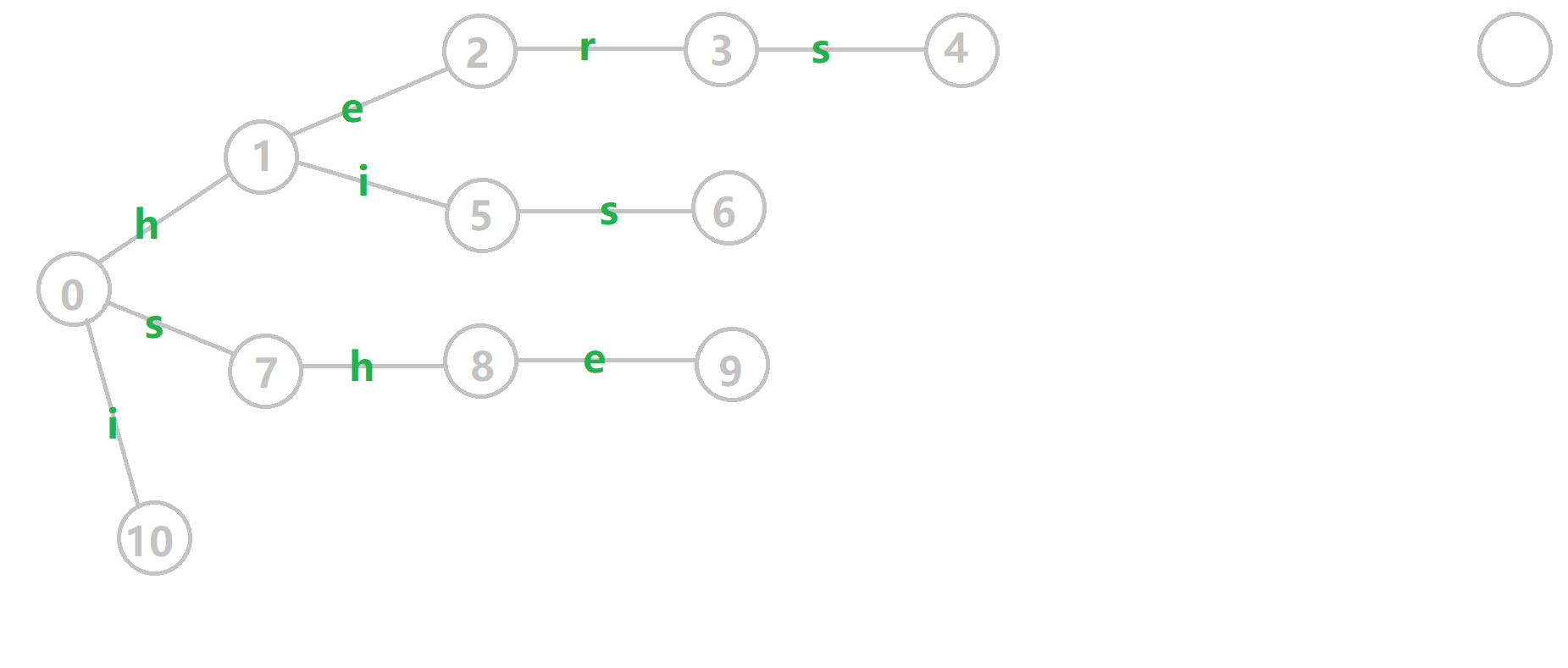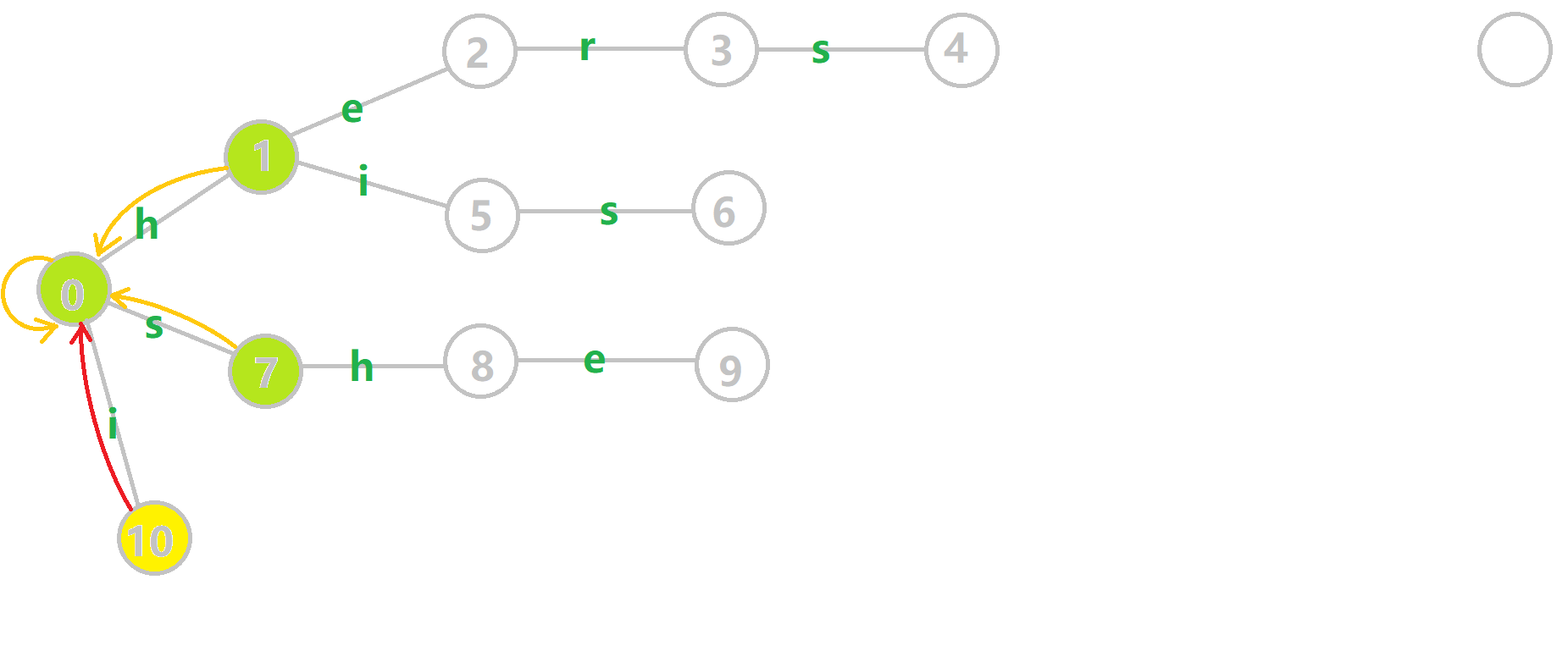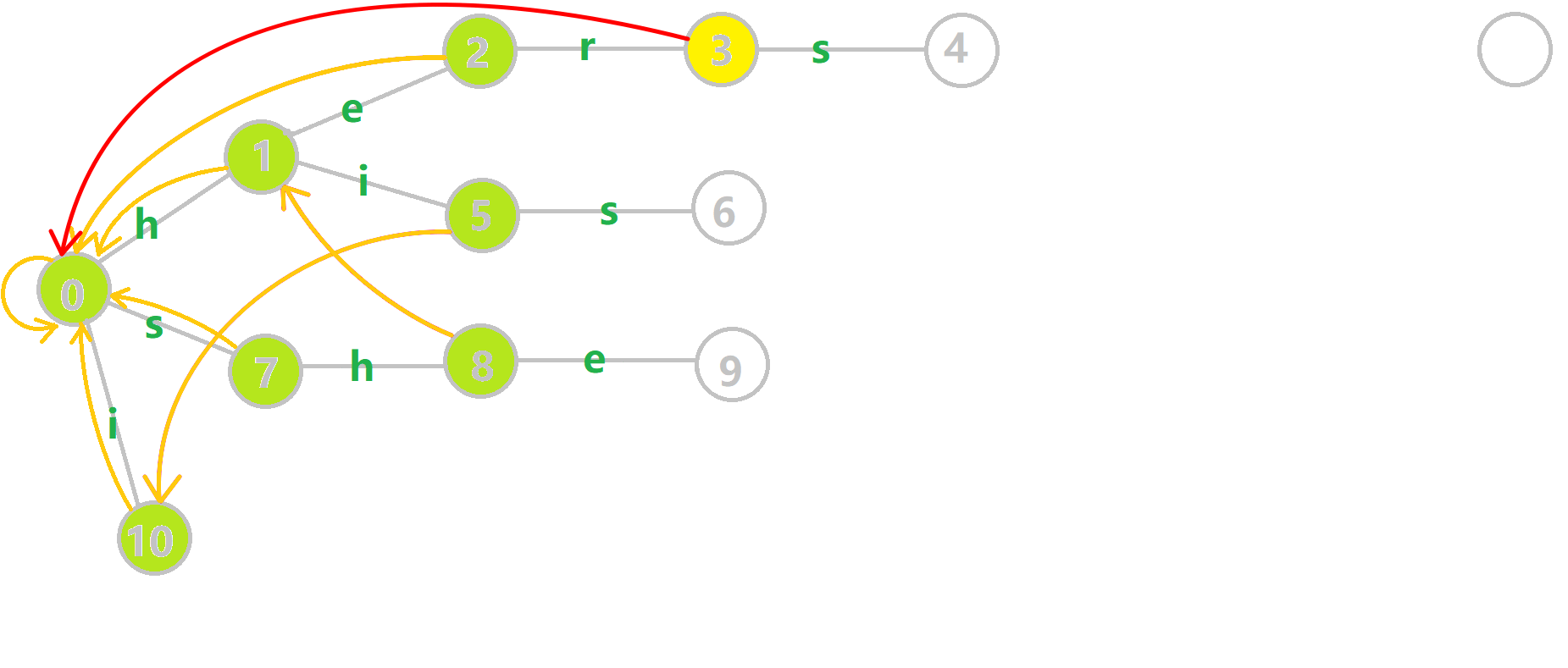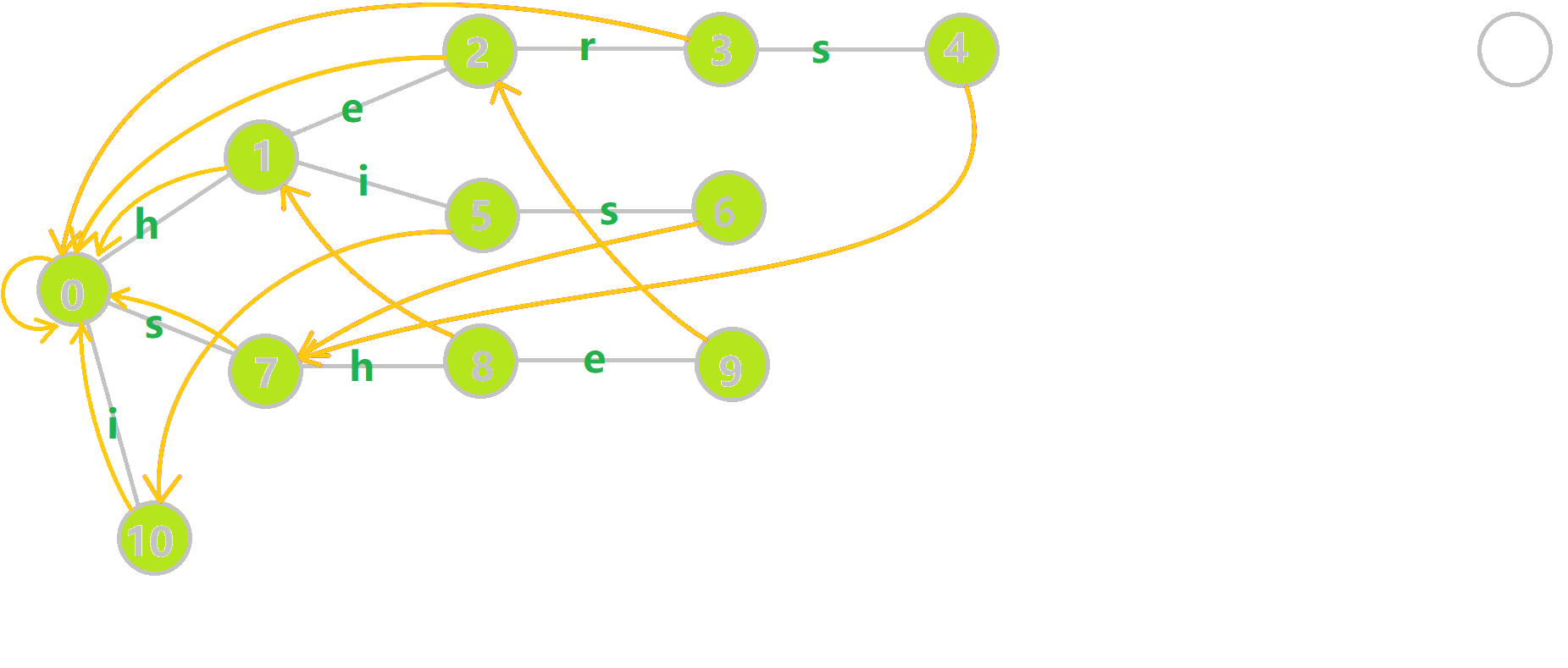
重点分析一下 \(6\) 的构建
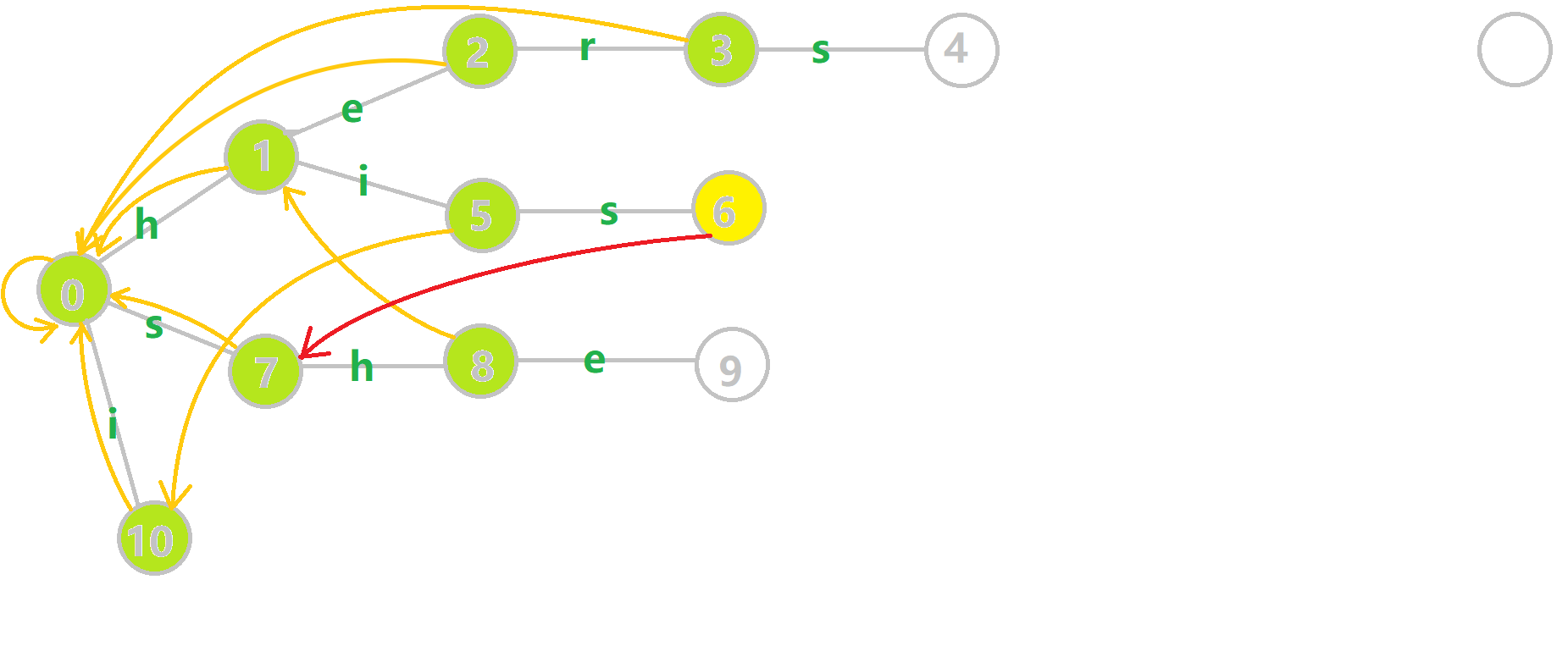
通过瞪眼法不难看出 \(fail[6]\) 应该指向结点 \(7\)。
分析一下算法流程,找到 \(6\) 的父节点 \(5\),\(fail[5] = 10\) 然而没有 \(s\) 的出边,所以继续跳 \(fail\) 指针,\(fail[10] = 0\),发现 \(0\) 有 \(s\) 的出边并指向 \(7\),所以 \(fail[6] = 7\)。
全部建完后的图是这样的:
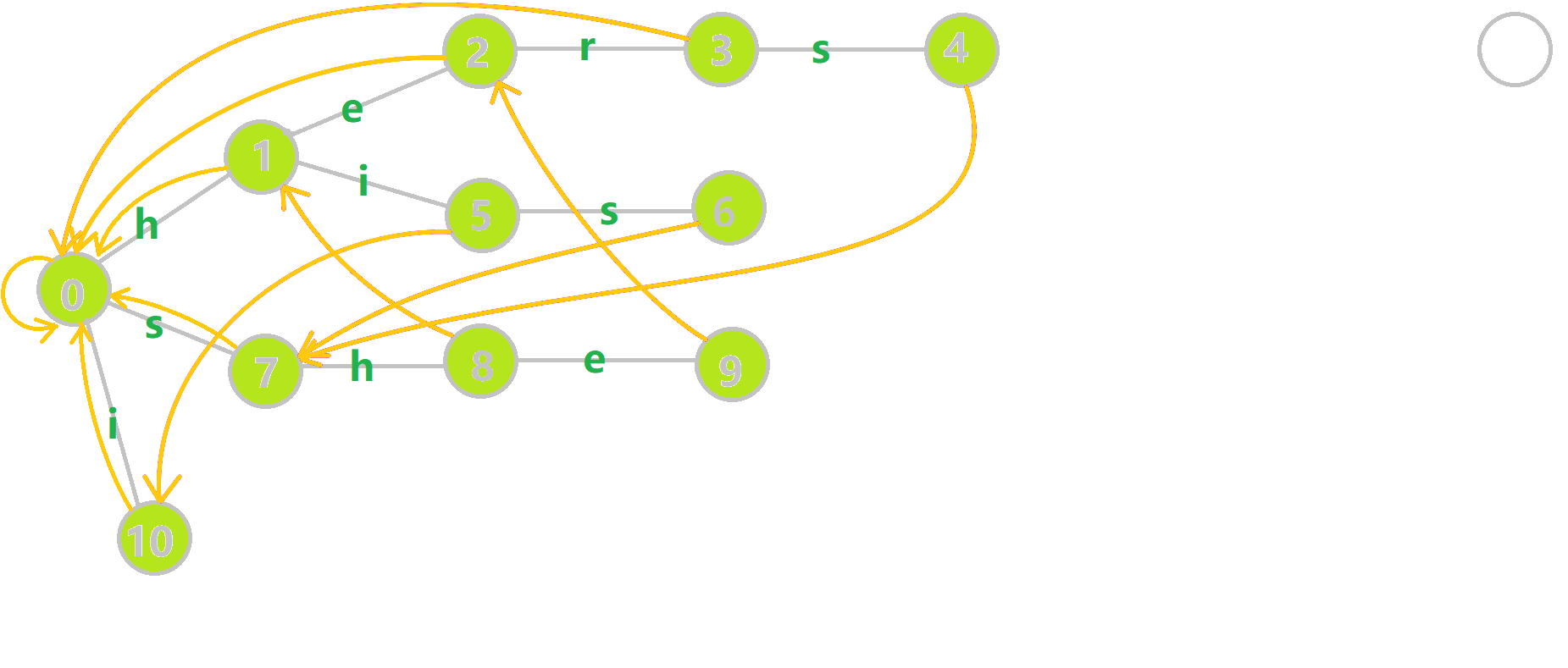
这样就完成了 \(fail\) 的构建,并得到一份比较暴力的构建方式,我们来看优化
字典树和字典图
先来看构建函数 build() ,该函数的目标有两个,一个是构建 fail 指针,一个是构建自动机。
void build(){
for(int i = 0; i < 26; ++i) if(tr[0][i]) q.push(tr[0][i]); // tr[0][i] 都指向 0 结点,所以不用赋初值
//如果存在这个边就入队
while(!q.empty()){
int u = q.front(); q.pop();
for(int i = 0; i < 26; ++i){
if(tr[u][i]) fail[tr[u][i]] = tr[fail[u]][i], q.push(tr[u][i]);
//按照上面所说的方式更新fail指针
else tr[u][i] = tr[fail[u]][i];//这是那个优化,后面会讲
}
}
}
我们是通过 bfs 构建 fail 指针的,而 fail 指针一定是由深度深的点指向深度浅的点。
我们由已经构建完成的点去构建未构建的点,假设我们当前的已经构建完成的一个状态是 \(u\),通过字符 \(i\) 指向下一个状态。
- 如果存在下一个状态 \(tr[u][i]\),那么就让 \(fail[tr[u][i]]\) 指向 \(tr[fail[u]][i]\)。
正确性应该比较显然,如果 \(u\) 失配了会指向 \(fail[u]\),那么在 \(u\) 后面接了一个状态 \(i\) 后再失配就应该指向 \(fail[u]\) 在后面接一个状态 \(i\) 在失配的位置。
那如果没有这个位置怎么办?\(fail[u]\) 的深度一定比 \(u\) 的深度浅,所以它已经被处理完了,如果 \(tr[fail[u]][i]\) 有值,那么要么是它在 \(fail[u]\) 的模式串下在后面接一个字符 \(i\),要么是在 \(fail[fail[u]]\) 的模式串下在后面接一个字符 \(i\),...。不断这么递归,就算最终也没有,那也只能说明指向了根节点,并不影响正确性。 - 如果不存在下一个状态 \(tr[u][i]\),我们让它指向 \(tr[fail[u]][i]\),就是为了保证上面第一种情况的正确性。并且通过这步操作,我们可以在匹配的过程中自动跳 \(fail\) 指针,不必再单独进行判断。
原来的构建方法可以通过 \(while\) 循环寻找 \(fail\) 结点实现,循环太多次导致复杂度太高
上面提到的优化就是通过else语句的代码修改了字典树的结构。
而它将不存在的字典树状态链连接到失配指针的对应状态。使得再次遍历这里的时候会继续向下跳转,起到一个通过继续开链来压缩路径的效果,这样就能节省很多时间。
这样 AC 自动机修改字典树结构连出的边就会使字典树变为字典图。
如果有人想看更杂乱更加形象的图的话:
其中:
- 蓝色结点:BFS 遍历到的结点 u
- 蓝色的边:当前结点下,AC 自动机修改字典树结构连出的边。
- 黑色的边:AC 自动机修改字典树结构连出的边。
- 红色的边:当前结点求出的 fail 指针
- 黄色的边:fail 指针
- 灰色的边:字典树的边
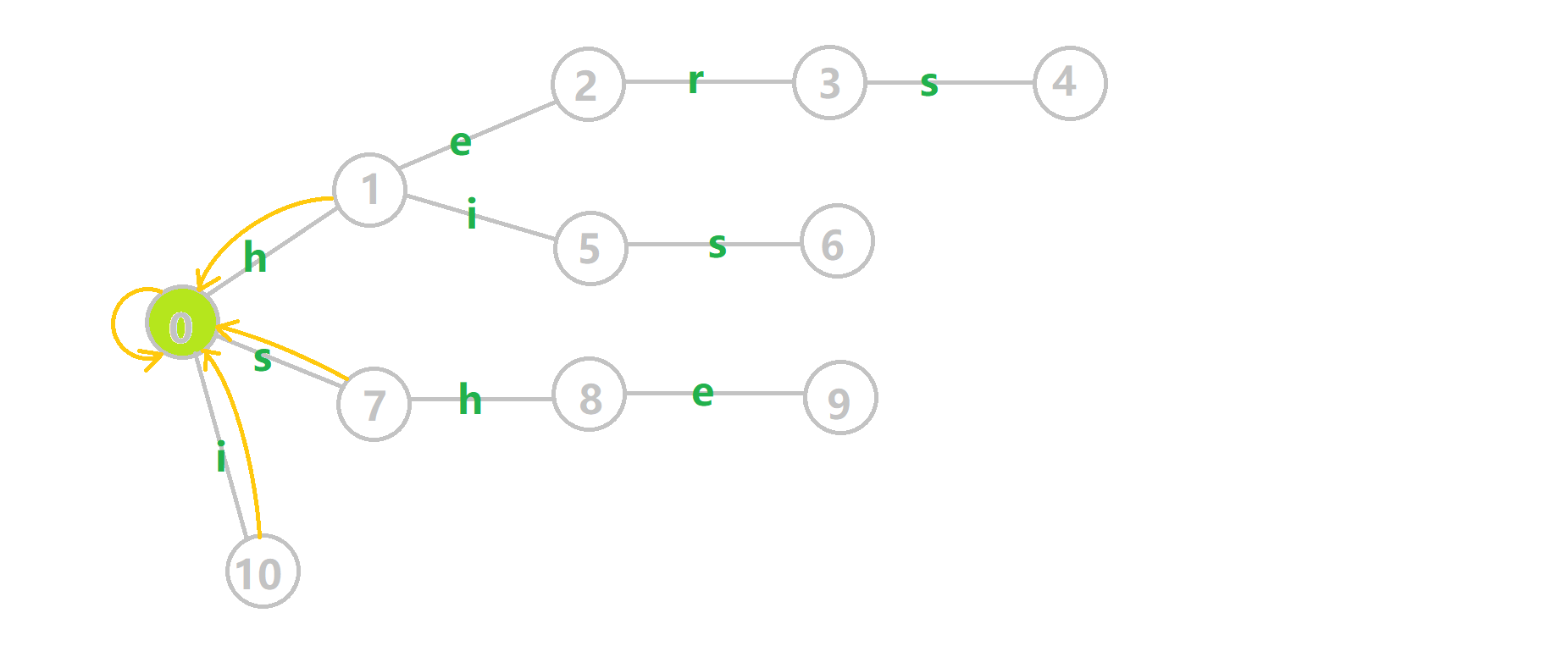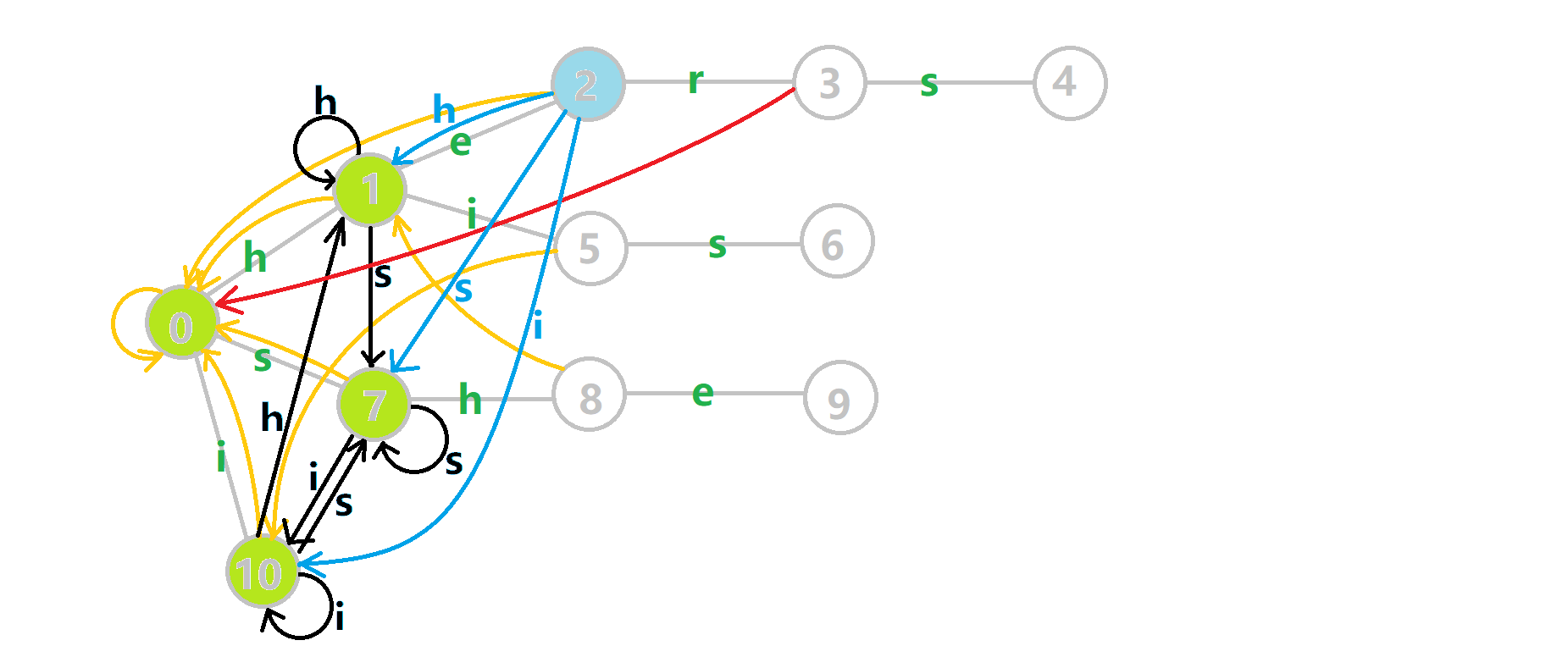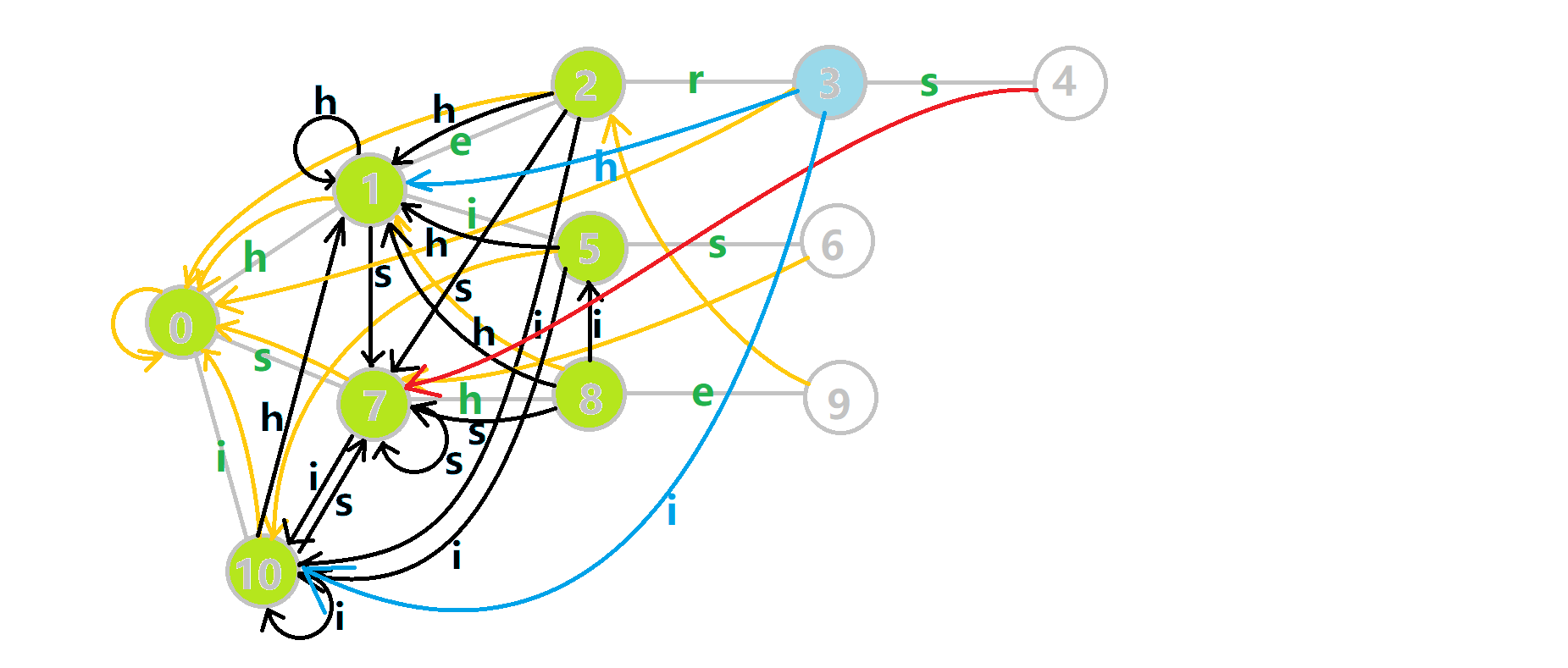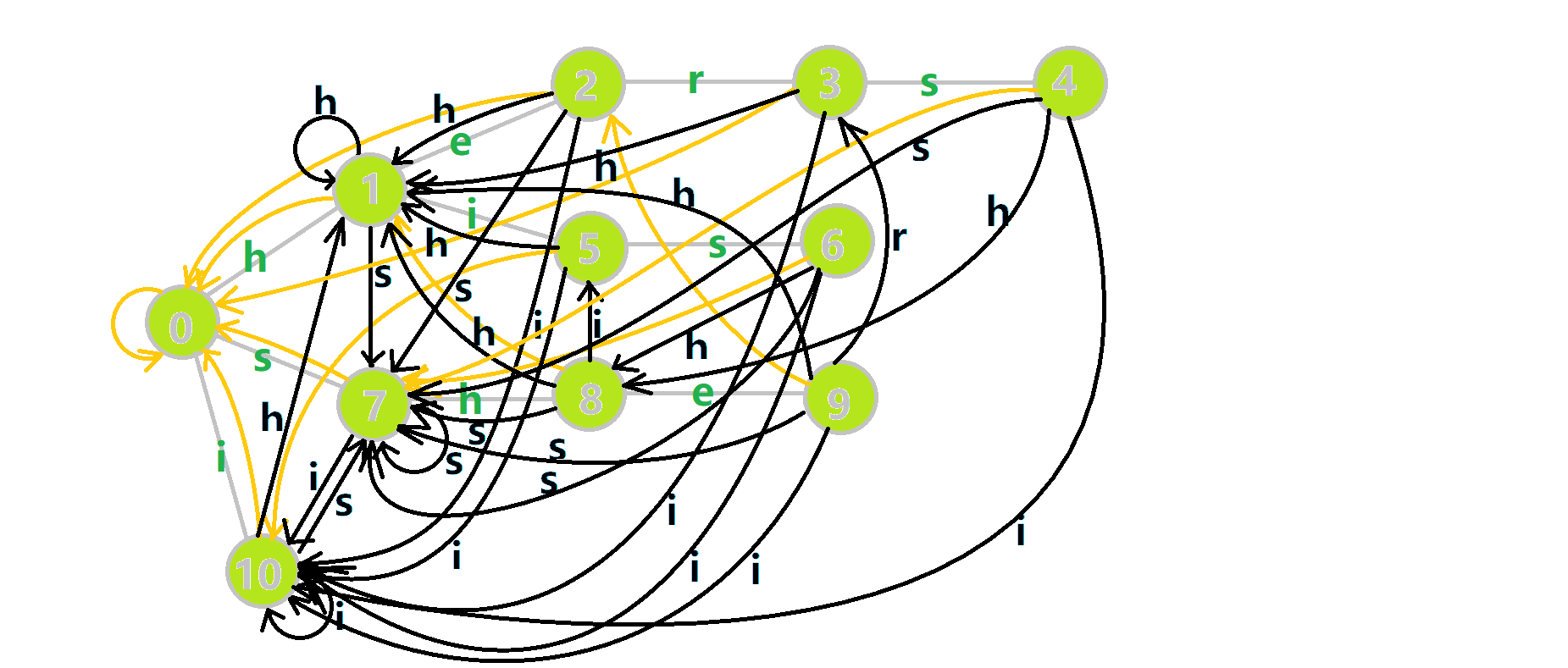
可以发现,众多交错的黑色边将字典树变成了 字典图。图中省略了连向根结点的黑边(否则会更乱)。我们重点分析一下结点 5 遍历时的情况。我们求 \(tr[5][s]\) 的 fail 指针:
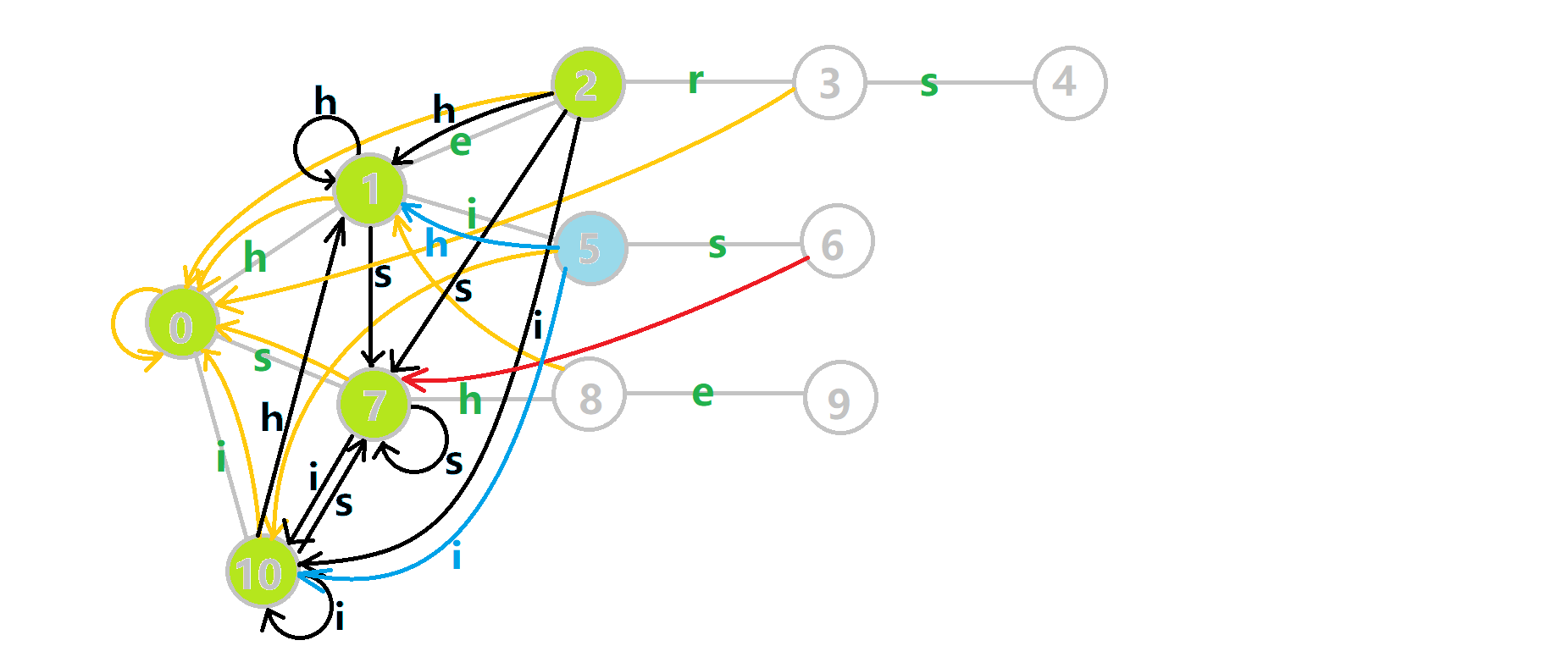
本来的策略是找 fail 指针,于是我们跳到 \(fail[5] = 10\) 发现没有 s 连出的字典树的边,于是跳到 \(fail[10] = 0\),发现有 \(tr[0][s] = 7\) ,于是 \(fail[6] = 7\) ;但是有了黑边、蓝边,我们跳到 \(fail[5] = 10\) 之后直接走 \(tr[10][s] = 7\) 就走到 \(7\) 号结点了。
这就是 build 完成的两件事:构建 fail 指针和建立字典图。这个字典图也会在查询的时候起到关键作用。
在贴一个最终状态的图。这张图真是令人作呕
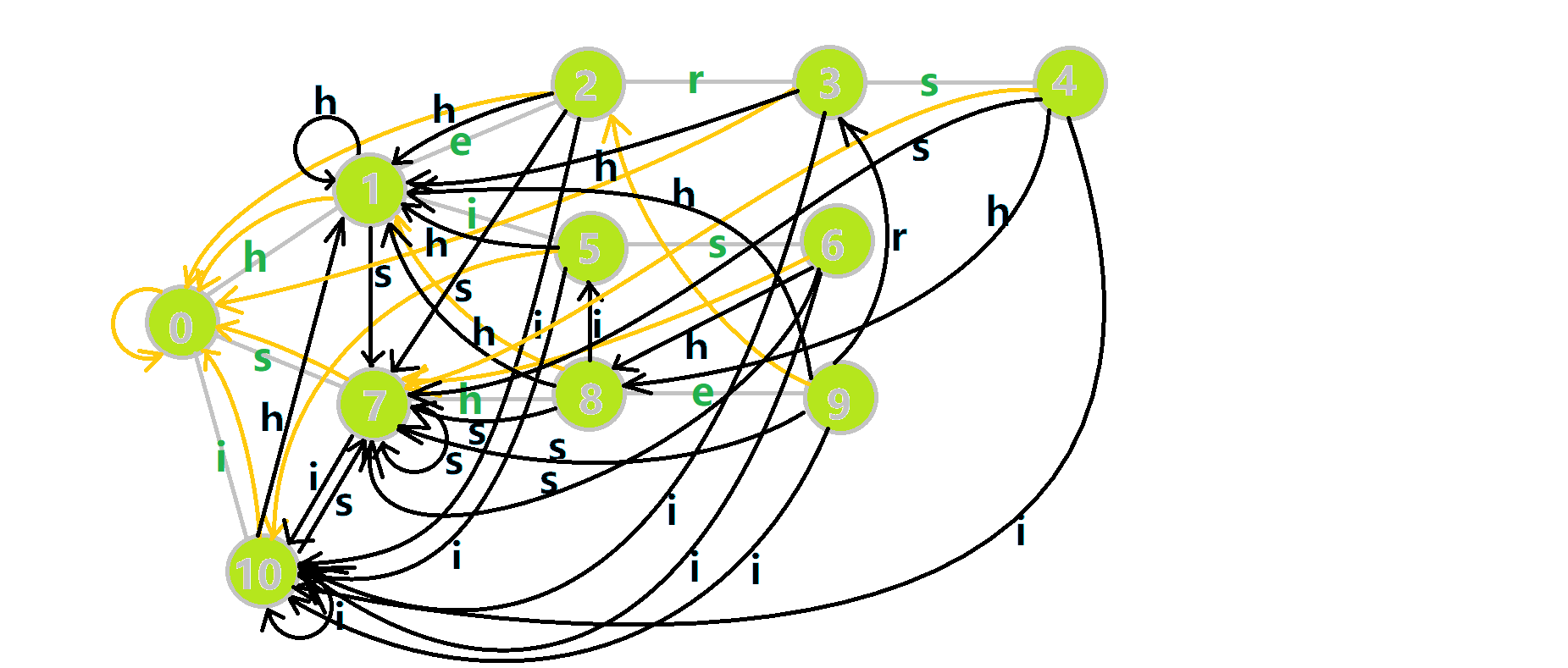
多模式匹配
(这只是对于引例的query函数,具体题目的函数写法可能不太相同)
int query(char *t){
int u = 0, res = 0;
for(int i = 1; t[i]; ++i){
u = tr[u][t[i] - 'a'];
for(int j = u; j && e[j] != -1; j = fail[j]){
res += e[j], e[j] = -1;
}
}
return res;
}
这里 \(u\) 作为字典树上当前匹配到的结点, \(res\) 即返回的答案。循环遍历匹配串, \(u\) 在字典树上跟踪当前字符。利用 \(fail\) 指针找出所有匹配的模式串,累加到答案中。然后清零。对 \(cnt[j]\) 取反的操作用来判断 \(cnt[j]\) 是否等于 \(-1\)。在上文中我们分析过,字典树的结构其实就是一个 \(trans\) 函数,而构建好这个函数后,在匹配字符串的过程中,我们会舍弃部分前缀达到最低限度的匹配。\(fail\) 指针则指向了更多的匹配状态。
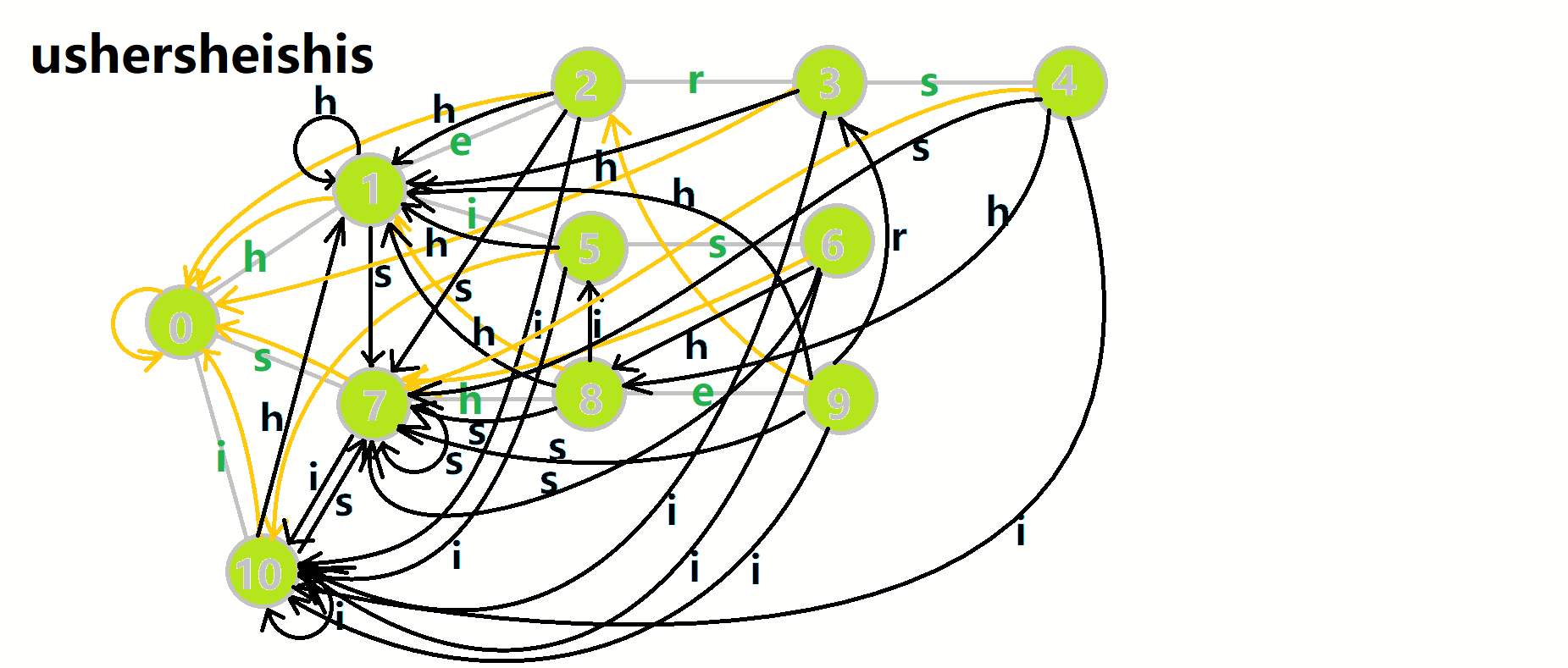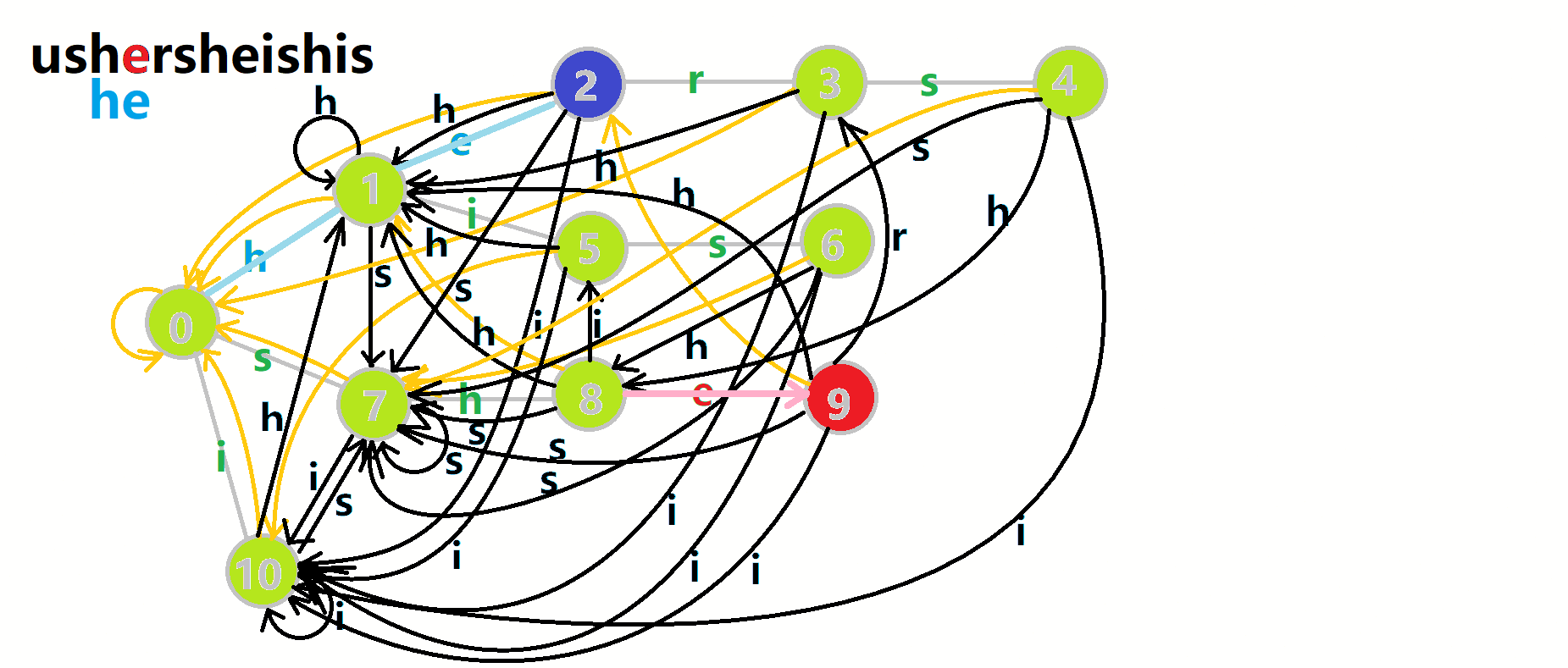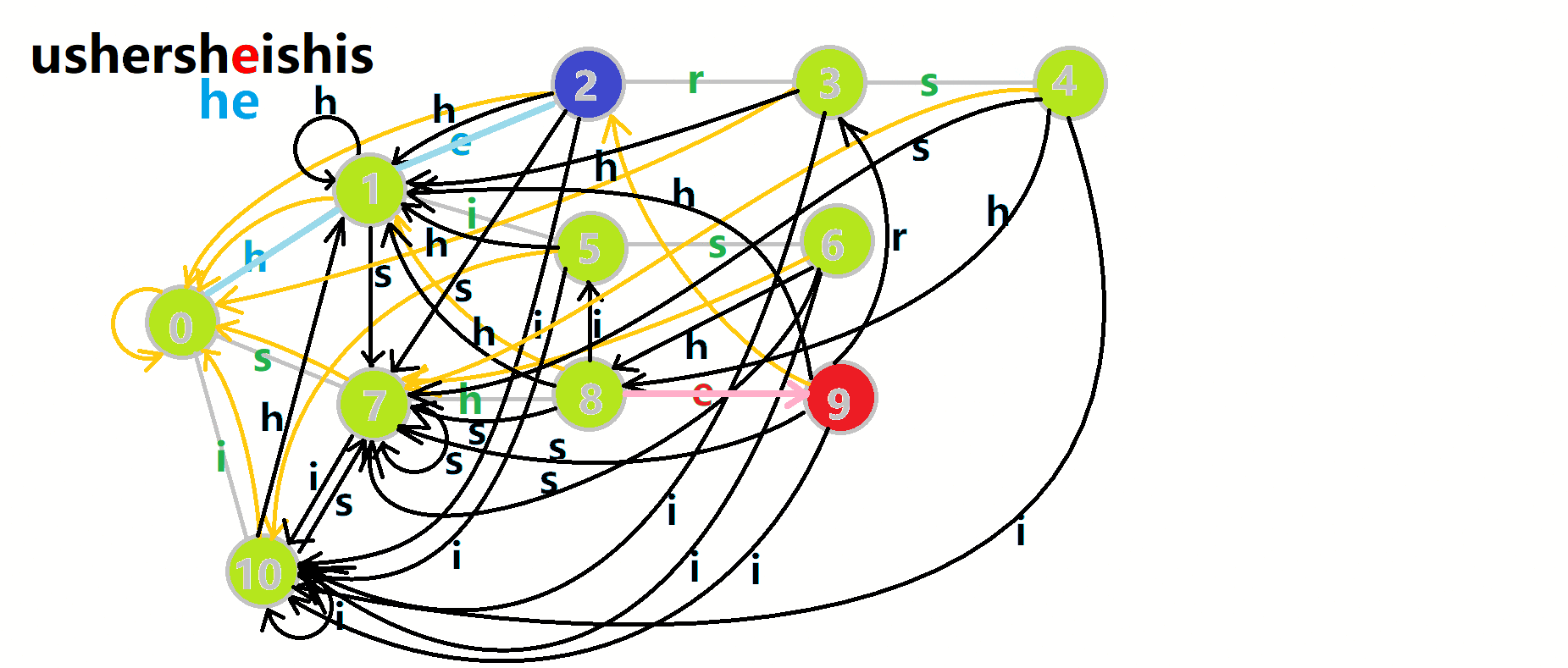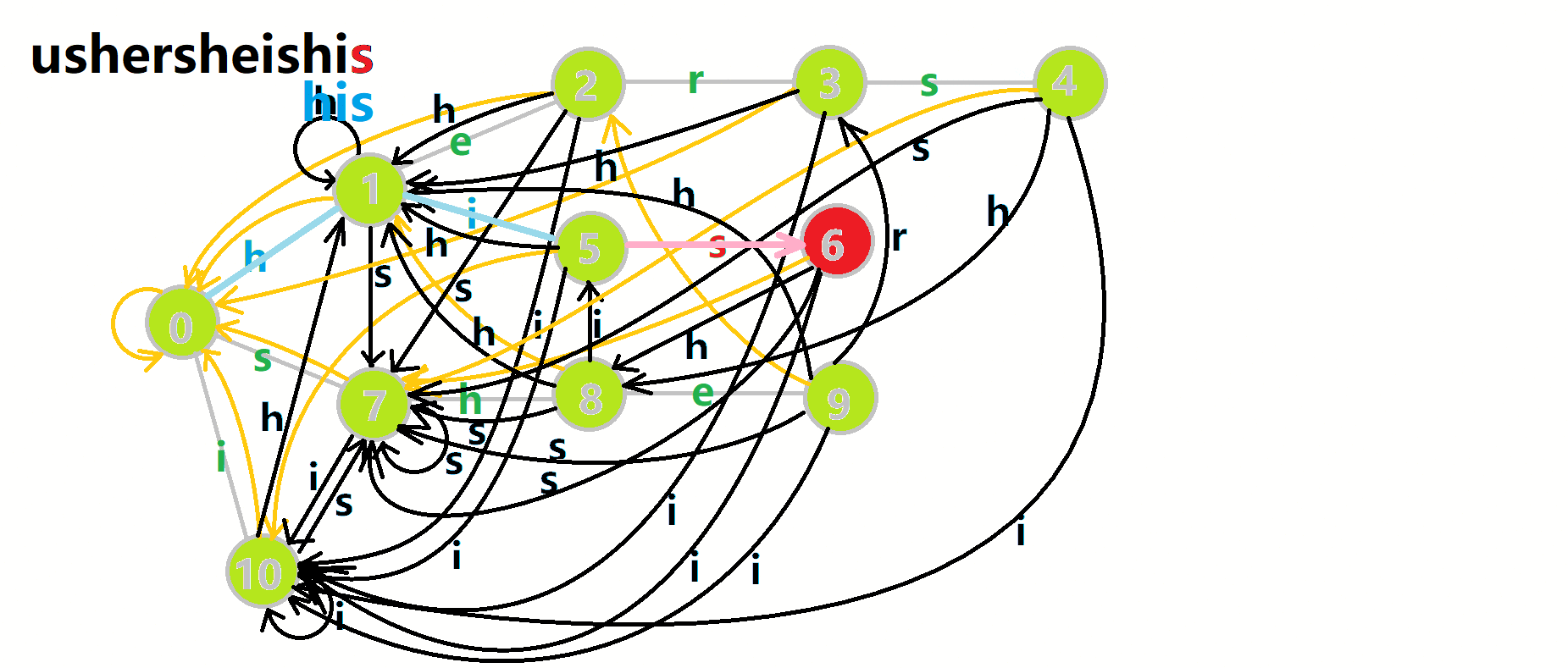
更加形象的匹配过程:
其中:
- 红色结点: \(p\) 结点
- 粉色箭头: \(p\) 在自动机上的跳转,
- 蓝色的边:成功匹配的模式串
- 蓝色结点:示跳 fail 指针时的结点(状态)。
例题
P3808 【模板】AC自动机(简单版)
做法即上面的引例,这里不再详细介绍。
P3796 【模板】AC自动机(加强版)
Solution
保证不会存在相同的字符串,那么在插入的末尾标记一下这是第几个字符串。
在询问的时候,对于每个状态不断跳 \(fail\) 指针找到它的所有状态,把遇到的末尾标记对应记录一个 \(cnt\) 进行累加统计。
最后扫一遍 \(cnt\) 的数组找出最大值
Code
/*
Work by: Suzt_ilymics
Knowledge: ??
Time: O(??)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 1e6+5;
const int INF = 1e9+7;
const int mod = 1e9+7;
int n;
char s[220][77];
char t[MAXN];
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
namespace AC {
int tr[MAXN][26], tot = 0;
int e[MAXN], cnt[MAXN], fail[MAXN];
queue<int> q;
void Clear() {
memset(tr, false, sizeof tr);
memset(e, false, sizeof e);
memset(cnt, false, sizeof cnt);
memset(fail, false, sizeof fail);
tot = 0;
}
void Insert(char *s, int id) {
int now_ = 0;
for(int i = 1; s[i]; ++i) {
if(!tr[now_][s[i] - 'a']) tr[now_][s[i] - 'a'] = ++tot;
now_ = tr[now_][s[i] - 'a'];
}
e[now_] = id;
}
void Get_fail() {
for(int i = 0; i < 26; ++i) if(tr[0][i]) q.push(tr[0][i]);
while(!q.empty()) {
int u = q.front(); q.pop();
for(int i = 0; i < 26; ++i) {
if(tr[u][i]) fail[tr[u][i]] = tr[fail[u]][i], q.push(tr[u][i]);
else tr[u][i] = tr[fail[u]][i];
}
}
}
void Query(char *t) {
int u = 0;
for(int i = 1; t[i]; ++i) {
u = tr[u][t[i] - 'a'];
for(int j = u; j; j = fail[j]) cnt[e[j]]++;
}
}
}
int main()
{
while(true) {
AC::Clear();
n = read();
if(!n) return 0;
for(int i = 1; i <= n; ++i) scanf("%s", s[i] + 1), AC::Insert(s[i], i);
scanf("%s", t + 1);
AC::Get_fail();
AC::Query(t);
int Max = -1;
for(int i = 1; i <= n; ++i) Max = max(Max, AC::cnt[i]);
printf("%d\n", Max);
for(int i = 1; i <= n; ++i) if(Max == AC::cnt[i]) printf("%s\n", s[i] + 1);
}
return 0;
}
P5357 【模板】AC自动机(二次加强版)
Solution
显然此时暴跳已经不能满足我们的需求,毕竟随便一个 \(aaa...aaa\) 的串就能把我们卡成 \(O(n^2)\) 的。
我们发现 \(fail\) 指针总是由深度深的点指向深度浅的点,那么所有 \(u\) 向 \(fail[u]\) 的连边就恰好构成了一个 \(DAG\),那么我们可以在匹配到每个节点的时候先不调 \(fail\) 指针,只是标记一下,留到最后一起跳。那样就可以做到线性的复杂度了。
Code
/*
Work by: Suzt_ilymics
Problem: 不知名屑题
Knowledge: 垃圾算法
Time: O(能过)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 2e6+5;
const int INF = 1e9+7;
const int mod = 1e9+7;
int n;
char s[MAXN];
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
namespace AC {
int tr[MAXN][26], tot = 0;
int fail[MAXN], e[MAXN], cnt[MAXN], pre[MAXN], id[MAXN];
queue<int> q;
void Insert(char *s, int bh) {
int u = 0;
for(int i = 1; s[i]; ++i) {
if(!tr[u][s[i] - 'a']) tr[u][s[i] - 'a'] = ++ tot;
u = tr[u][s[i] - 'a'];
}
e[u]++;
pre[bh] = u;
}
void Get_fail() {
for(int i = 0; i < 26; ++i) if(tr[0][i]) q.push(tr[0][i]);
while(!q.empty()) {
int u = q.front(); q.pop();
for(int i = 0; i < 26; ++i) {
if(tr[u][i]) fail[tr[u][i]] = tr[fail[u]][i], q.push(tr[u][i]), id[fail[tr[u][i]]]++;
else tr[u][i] = tr[fail[u]][i];
}
}
}
void Query(char *s) {
int u = 0;
for(int i = 1; s[i]; ++i) {
u = tr[u][s[i] - 'a'];
cnt[u]++;
}
}
void Topsort() {
for(int i = 1; i <= tot; ++i) if(!id[i]) q.push(i);
while(!q.empty()) {
int u = q.front(); q.pop();
int v = fail[u];
cnt[v] += cnt[u];
if(!--id[v]) q.push(v);
}
}
}
int main()
{
n = read();
for(int i = 1; i <= n; ++i) {
scanf("%s", s + 1);
AC::Insert(s, i);
}
AC::Get_fail();
scanf("%s", s + 1);
AC::Query(s);
AC::Topsort();
for(int i = 1; i <= n; ++i) {
printf("%d\n", AC::cnt[AC::pre[i]]);
}
return 0;
}
P2444 [POI2000]病毒
Solution
如何确定它是安全的?
找到一个循环节,使他永远不会循环到一个结尾结点。可以用 dfs 判环。
注意,如果一个结点的 \(fail\) 指针被标记,那么它也是危险的,也应该被标记。
因为这个结点的 \(fail\) 指针指向的模式串是这个结点所对应的模式串的后缀。
Code
/*
Work by: Suzt_ilymics
Problem: 不知名屑题
Knowledge: 垃圾算法
Time: O(能过)
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#define LL long long
#define orz cout<<"lkp AK IOI!"<<endl
using namespace std;
const int MAXN = 1e6+5;
const int INF = 1e9+7;
const int mod = 1e9+7;
int n;
char s[MAXN];
int read(){
int s = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) f |= (ch == '-'), ch = getchar();
while(isdigit(ch)) s = (s << 1) + (s << 3) + ch - '0' , ch = getchar();
return f ? -s : s;
}
namespace AC {
int tr[MAXN][2], tot = 0;
int fail[MAXN], e[MAXN];
bool vis[MAXN], f[MAXN];
queue<int> q;
void Insert(char *s) {
int u = 0;
for(int i = 1; s[i]; ++i) {
if(!tr[u][s[i] - '0']) tr[u][s[i] - '0'] = ++ tot;
u = tr[u][s[i] - '0'];
}
e[u] ++;
}
void Get_fail() {
for(int i = 0; i < 2; ++i) if(tr[0][i]) q.push(tr[0][i]);
while(!q.empty()) {
int u = q.front(); q.pop();
for(int i = 0; i < 2; ++i) {
if(tr[u][i]) {
fail[tr[u][i]] = tr[fail[u]][i], q.push(tr[u][i]);
if(e[fail[tr[u][i]]]) e[tr[u][i]]++;
}
else tr[u][i] = tr[fail[u]][i];
}
}
}
bool dfs(int u) {
vis[u] = true;
for(int i = 0; i < 2; ++i) {
if(vis[tr[u][i]]) return true;
if(!e[tr[u][i]] && !f[tr[u][i]]) {
f[tr[u][i]] = true;
if(dfs(tr[u][i])) return true;
}
}
vis[u] = false;
return false;
}
}
int main()
{
n = read();
for(int i = 1; i <= n; ++i) scanf("%s", s + 1), AC::Insert(s);
AC::Get_fail();
AC::dfs(0) ? puts("TAK") : puts("NIE");
return 0;
}
其他例题
P5231 [JSOI2012]玄武密码
P2292 [HNOI2004]L语言
P3121 [USACO15FEB]Censoring G
P3311 [SDOI2014] 数数 AC 自动机 + 数位 DP
CF163E e-Government AC 自动机 + 线段树
P7582 「RdOI R2」风雨(rain) 比 CF163E 更恶心
P2414 [NOI2011] 阿狸的打字机
写在后面
如有不懂或错误烦请指出,我会在最快的时间处理。
最后,屑题单求收藏qwq

 乘上与平时相反的列车,为了去见从未见过的风景。
乘上与平时相反的列车,为了去见从未见过的风景。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号