树链剖分
前置芝士
dfs序,线段树
正文
树链剖分就是通过划分轻重边将树分割成许多链,然后利用数据结构(线段树)来维护这些链
使得在树上可以用非常优秀的复杂度去遍历一些信息
(本质上是一种优化暴力(就像LCA)(其实所有数据结构都是优化的暴力))
首先明确的概念
重儿子:父亲节点的所有儿子中子树结点数目最多(size最大)的结点;(节点数目包括自身)
轻儿子:父亲节点中除了重儿子以外的儿子;
重边:父亲结点和重儿子连成的边;
轻边:父亲节点和轻儿子连成的边;
重链:由多条重边连接而成的路径;
轻链:由多条轻边连接而成的路径;
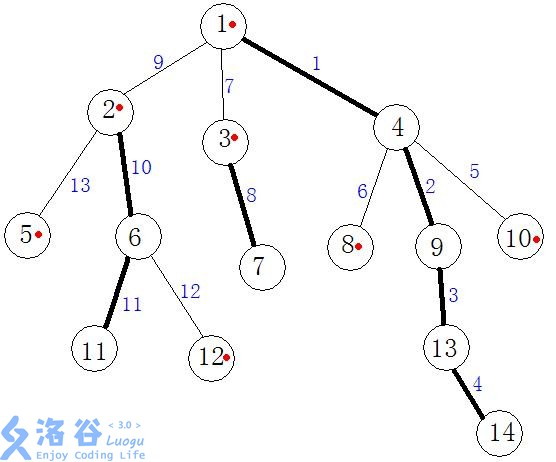
比如上面这幅图中,用黑线连接的结点都是重结点,其余均是轻结点,
2-11就是重链,2-5就是轻链,用红点标记的就是该结点所在重链的起点,也就是下文提到的top结点,
还有每条边的值其实是进行dfs时的执行序号。
树链剖分的思路
将一棵每个节点的儿子按照儿子大小划分成重儿子和轻儿子(其他儿子),将树划分成一条条链(重链和轻链)
利用dfs序,将同一个链上的点放在一起,在建出线段树
使得在调用两点的简单路径时,可以一跳跳过多个节点(类比LCA思考)
从而达到减小复杂度的目的
如何实现
有不理解的地方,手模是个不错的选择
1、先跑第一遍DFS(初始化)
每遍历到一个点,让siz为1,记录父亲与深度
然后回溯的时候加上其子树的点的大小
并顺便在遍历到的子树中挑出重儿子
1 void dfs(int x, int fa){// 2 siz[x] = 1, fath[x] = fa, dep[x] = dep[fa] + 1;//确定以x为根的子树的大小,父亲,深度 3 //cout<<cnt<<"lzx"<<x<<" "<<fa<<endl; 4 for(int i = head[x]; i; i = e[i].nxt){//类似于lca初始化的遍历 5 int v = e[i].to; 6 if(v == fa) continue; 7 dfs(v, x); 8 siz[x] += siz[v];//回溯的时候更新子树大小 9 if(siz[son[x]] < siz[v]) son[x] = v;//挑出重儿子 10 } 11 }
2、在跑一遍DFS(分链)
确定dfs序,并把dfs序所对应的元素用pre数组存起来
注意遍历顺序,因为开始我们提到划分重链,所以我们要优先遍历重儿子,并把链顶元素也传下去(先遍历重儿子感觉珂以使复杂度最优)
遍历完重儿子后,再遍历其他儿子,并新开一条链
1 void dfs2(int x, int tp){//分链,tp表示该链的顶端 2 top[x] = tp, dfn[x] = ++cnt, pre[cnt] = x;//确定x节点的链的顶端是tp,x的dfs序及反dfs序 3 if(son[x]) dfs2(son[x], tp);//为了使重链的dfn在一起,要先遍历重儿子 4 for(int i = head[x]; i; i = e[i].nxt){ 5 int v = e[i].to; 6 if(v == fath[x] || son[x] == v) continue;//如果一个点的fa等于自己或者下一个点是它的重儿子就跳过 7 //(如果是重儿子的话应该在以前就已经遍历了,所以还有防止在遍历一遍的作用 8 dfs2(v, v);//新开一条链 9 } 10 }
3、数据维护
我们不难发现,每个重链的dfs序是连在一起的,那么我们是不是可以考虑用线段树来维护它,因为线段树刚好可以维护一段连续的区间
线段树板中板

1 #define lson i << 1 2 #define rson i << 1 | 1 3 struct Tree{//和,懒标记,长度 4 int sum, lazy, len; 5 }tree[MAXN << 2]; 6 void push_up(int i){//上传标记 7 tree[i].sum = (tree[lson].sum + tree[rson].sum) % p; 8 return ; 9 } 10 void build(int i, int l , int r){//建树 11 tree[i].lazy = 0, tree[i].len = r - l + 1; 12 if(l == r) { 13 tree[i].sum = a[pre[l]] % p; 14 return ; 15 } 16 int mid = l + r >> 1; 17 build(lson, l, mid), build(rson, mid + 1, r); 18 push_up(i); 19 return ; 20 } 21 void pushdown(int i){//下传懒标记 22 if(tree[i].lazy){ 23 tree[lson].lazy = (tree[lson].lazy + tree[i].lazy) % p; 24 tree[rson].lazy = (tree[rson].lazy + tree[i].lazy) % p; 25 tree[lson].sum = (tree[lson].sum + tree[i].lazy * tree[lson].len) % p; 26 tree[rson].sum = (tree[rson].sum + tree[i].lazy * tree[rson].len) % p; 27 tree[i].lazy = 0; 28 } 29 return ; 30 } 31 void add(int i, int l, int r, int L, int R, int k){ 32 //lr表示遍历到的区间,LR表示查询到的区间 33 if(L <= l && r <= R) { 34 tree[i].sum = (tree[i].sum + (k * tree[i].len) % p) % p; 35 tree[i].lazy += k; 36 return ; 37 } 38 //cout<<l<<" "<<R << " "<< r<< " "<<L<<"lkp"<<endl; 39 if(l > R || r < L) return ; 40 pushdown(i); 41 int mid = (l + r) >> 1; 42 if(L <= mid) add(lson, l, mid, L, R, k); 43 if(R > mid) add(rson, mid + 1, r, L, R, k); 44 push_up(i); 45 return ; 46 } 47 int get(int i, int l, int r, int L, int R){ 48 int sum = 0; 49 if(L <= l && r <= R) { 50 return tree[i].sum % p; 51 } 52 if(l > R || r < L) return 0; 53 pushdown(i); 54 int mid = (l + r) >> 1; 55 if(mid >= L) sum = (sum + get(lson, l, mid, L, R)) % p; 56 if(mid < R) sum = (sum + get(rson, mid + 1, r, L, R)) % p; 57 return sum % p; 58 }
那么怎么更改信息呢
(更改方式有点像倍增求LCA,珂以类比理解)
如果两个元素不在同一条链上,
将链顶深的元素一直向上跳,并在线段树中进行修改(提取)信息的操作
如果两个元素在同一条链上,直接进行修改(提取)信息的操作
1 void change(int x, int y, int k){ 2 while (top[x] != top[y]){//如果两个点的链顶不相同(感觉和LCA的处理有点类似 3 if(dep[top[x]] < dep[top[y]]) swap(x, y); 4 Seg::add(1, 1, n, dfn[top[x]], dfn[x], k);//先改变深度浅的 5 x = fath[top[x]];//向上跳到链顶的父亲 6 } 7 if(dfn[x] > dfn[y]) swap(x, y);//最后肯定是在一条链上 8 Seg::add(1, 1, n, dfn[x], dfn[y], k); 9 return ; 10 } 11 int ask(int x, int y){ 12 int ans = 0; 13 while(top[x] != top[y]){//道理和change函数类似 14 if(dep[top[x]] < dep[top[y]]) swap(x, y);//先跳深度深度 15 ans = (ans + Seg::get(1, 1, n, dfn[top[x]], dfn[x])) % p; 16 x = fath[top[x]]; 17 } 18 if(dfn[x] > dfn[y]) swap(x, y); 19 ans = (ans + Seg::get(1, 1, n, dfn[x], dfn[y])) % p; 20 return ans % p; 21 }
例题的AC代码
namespace相当于把一部分函数进行组合包装,珂以有效区分函数作用,并避免重变量名
调用的时候和std类似,用***::即可
1 /* 2 Work by: Suzt_ilymics 3 Knowledge: 树链剖分 4 Time: O(nlog^2n) 5 */ 6 #include<iostream> 7 #include<cstdio> 8 #define int long long 9 using namespace std; 10 const int MAXN = 1e5+5; 11 int n, m, r, p; 12 int a[MAXN], pre[MAXN], siz[MAXN], son[MAXN], dep[MAXN], fath[MAXN], top[MAXN], dfn[MAXN]; 13 14 int read(){//因一个逗号写挂了的快读 15 /*int s=0,w=1; 16 char ch=getchar(); 17 while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();} 18 while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar(); 19 return s*w; 20 */ 21 int s = 0, w = 1; 22 char ch = getchar(); 23 //while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();} 24 while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();} 25 while(ch >= '0' && ch <= '9') 26 s = s * 10 + ch - '0', ch = getchar(); 27 return s * w; 28 } 29 30 namespace Seg{//线段树板中板 31 #define lson i << 1 32 #define rson i << 1 | 1 33 struct Tree{//和,懒标记,长度 34 int sum, lazy, len; 35 }tree[MAXN << 2]; 36 void push_up(int i){//上传标记 37 tree[i].sum = (tree[lson].sum + tree[rson].sum) % p; 38 return ; 39 } 40 void build(int i, int l , int r){//建树 41 tree[i].lazy = 0, tree[i].len = r - l + 1; 42 if(l == r) { 43 tree[i].sum = a[pre[l]] % p; 44 return ; 45 } 46 int mid = l + r >> 1; 47 build(lson, l, mid), build(rson, mid + 1, r); 48 push_up(i); 49 return ; 50 } 51 void pushdown(int i){//下传懒标记 52 if(tree[i].lazy){ 53 tree[lson].lazy = (tree[lson].lazy + tree[i].lazy) % p; 54 tree[rson].lazy = (tree[rson].lazy + tree[i].lazy) % p; 55 tree[lson].sum = (tree[lson].sum + tree[i].lazy * tree[lson].len) % p; 56 tree[rson].sum = (tree[rson].sum + tree[i].lazy * tree[rson].len) % p; 57 tree[i].lazy = 0; 58 } 59 return ; 60 } 61 void add(int i, int l, int r, int L, int R, int k){ 62 //lr表示遍历到的区间,LR表示查询到的区间 63 if(L <= l && r <= R) { 64 tree[i].sum = (tree[i].sum + (k * tree[i].len) % p) % p; 65 tree[i].lazy += k; 66 return ; 67 } 68 //cout<<l<<" "<<R << " "<< r<< " "<<L<<"lkp"<<endl; 69 if(l > R || r < L) return ; 70 pushdown(i); 71 int mid = (l + r) >> 1; 72 if(L <= mid) add(lson, l, mid, L, R, k); 73 if(R > mid) add(rson, mid + 1, r, L, R, k); 74 push_up(i); 75 return ; 76 } 77 int get(int i, int l, int r, int L, int R){ 78 int sum = 0; 79 if(L <= l && r <= R) { 80 return tree[i].sum % p; 81 } 82 if(l > R || r < L) return 0; 83 pushdown(i); 84 int mid = (l + r) >> 1; 85 if(mid >= L) sum = (sum + get(lson, l, mid, L, R)) % p; 86 if(mid < R) sum = (sum + get(rson, mid + 1, r, L, R)) % p; 87 return sum % p; 88 } 89 } 90 91 namespace Cut{ 92 int num_edge = 0, cnt = 0, head[MAXN << 1] = {0}; 93 struct edge{ 94 int nxt, to, from; 95 }e[MAXN << 1]; 96 void add(int from, int to){ 97 e[++num_edge].to = to; 98 e[num_edge].from = from; 99 e[num_edge].nxt = head[from]; 100 head[from] = num_edge; 101 } 102 void dfs(int x, int fa){// 103 siz[x] = 1, fath[x] = fa, dep[x] = dep[fa] + 1;//确定以x为根的子树的大小,父亲,深度 104 //cout<<cnt<<"lzx"<<x<<" "<<fa<<endl; 105 for(int i = head[x]; i; i = e[i].nxt){//类似于lca初始化的遍历 106 int v = e[i].to; 107 if(v == fa) continue; 108 dfs(v, x); 109 siz[x] += siz[v];//回溯的时候更新子树大小 110 if(siz[son[x]] < siz[v]) son[x] = v;//挑出重儿子 111 } 112 } 113 //引入重链这个概念会使分的链最少,复杂度更优秀 114 void dfs2(int x, int tp){//分链,tp表示该链的顶端 115 top[x] = tp, dfn[x] = ++cnt, pre[cnt] = x;//确定x节点的链的顶端是tp,x的dfs序及反dfs序 116 if(son[x]) dfs2(son[x], tp);//为了使重链的dfn在一起,要先遍历重儿子 117 for(int i = head[x]; i; i = e[i].nxt){ 118 int v = e[i].to; 119 if(v == fath[x] || son[x] == v) continue;//如果一个点的fa等于自己或者下一个点是它的重儿子就跳过 120 //(如果是重儿子的话应该在以前就已经遍历了,所以还有防止在遍历一遍的作用 121 dfs2(v, v);//新开一条链 122 } 123 } 124 void change(int x, int y, int k){ 125 while (top[x] != top[y]){//如果两个点的链顶不相同(感觉和LCA的处理有点类似 126 if(dep[top[x]] < dep[top[y]]) swap(x, y); 127 Seg::add(1, 1, n, dfn[top[x]], dfn[x], k);//先改变深度深的 128 x = fath[top[x]];//向上跳到链顶的父亲 129 } 130 if(dfn[x] > dfn[y]) swap(x, y);//最后肯定是在一条链上 131 Seg::add(1, 1, n, dfn[x], dfn[y], k); 132 return ; 133 } 134 int ask(int x, int y){ 135 int ans = 0; 136 while(top[x] != top[y]){//道理和change函数类似 137 if(dep[top[x]] < dep[top[y]]) swap(x, y);//先跳深度深的 138 ans = (ans + Seg::get(1, 1, n, dfn[top[x]], dfn[x])) % p; 139 x = fath[top[x]]; 140 } 141 if(dfn[x] > dfn[y]) swap(x, y); 142 ans = (ans + Seg::get(1, 1, n, dfn[x], dfn[y])) % p; 143 return ans % p; 144 } 145 } 146 147 signed main() 148 { 149 //输入 150 n = read(), m = read(), r = read(), p = read(); 151 for(int i = 1; i <= n; ++i) a[i] = read(); 152 for(int i = 1, u, v; i <= n - 1; ++i) { 153 u = read(), v = read(); 154 //cout<<"bilibili"; 155 Cut::add(u, v), Cut::add(v, u); 156 } 157 //for(int i = 1; i <= Cut::num_edge; ++i) printf("%d %dwzd\n", Cut::e[i].from, Cut::e[i].to); 158 //初始化 159 Cut::dfs(r,0), Cut::dfs2(r, r), Seg::build(1, 1, n); 160 //操作 161 for(int i = 1, opt, x, y, k; i <= m; ++i){ 162 opt = read(); 163 if(opt == 1){ 164 x = read(), y = read(), k = read(); 165 Cut::change(x, y, k); 166 } 167 if(opt == 2){ 168 x = read(), y = read(); 169 printf("%lld\n", Cut::ask(x, y)); 170 } 171 if(opt == 3){ 172 x = read(), k = read(); 173 //cout<<dfn[x]<<" "<<siz[x]<<"zsf"<<endl; 174 Seg::add(1, 1, n, dfn[x], dfn[x] + siz[x] - 1, k); 175 } 176 if(opt == 4){ 177 x = read(); 178 printf("%lld\n", Seg::get(1, 1, n, dfn[x], dfn[x] + siz[x] - 1)); 179 } 180 181 } 182 return 0; 183 }
[ZJOI2008]树的统计
一个维护最大值的例题
自己犯得**错误:
看清数据范围,提交时把检验用的cout删掉,max在push_up的时候只需要取它两个儿子的最大值

1 /* 2 Work by: Suzt_ilymics 3 Knowledge: 树链剖分 4 Time: O(nlog^2n) 5 */ 6 #include<iostream> 7 #include<cstdio> 8 #include<string> 9 #include<cstdio> 10 #define int long long 11 using namespace std; 12 const int inf = -1000000000; 13 const int MAXN = 3e4+5; 14 int n, m; 15 string s; 16 int a[MAXN], pre[MAXN], siz[MAXN], son[MAXN], dep[MAXN], fath[MAXN], top[MAXN], dfn[MAXN]; 17 18 int read(){ 19 int s = 0, w = 1; 20 char ch = getchar(); 21 while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();} 22 while(ch >= '0' && ch <= '9') 23 s = s * 10 + ch - '0', ch = getchar(); 24 return s * w; 25 } 26 27 namespace Seg{ 28 #define lson i << 1 29 #define rson i << 1 | 1 30 struct Tree{ 31 int sum, lazy, len, max; 32 }tree[MAXN << 2]; 33 void push_up(int i){ 34 tree[i].sum = tree[lson].sum + tree[rson].sum; 35 tree[i].max = max(tree[lson].max, tree[rson].max); 36 return ; 37 } 38 void build(int i, int l , int r){ 39 tree[i].lazy = 0, tree[i].len = r - l + 1; 40 if(l == r) { 41 tree[i].sum = a[pre[l]]; 42 tree[i].max = a[pre[l]]; 43 return ; 44 } 45 int mid = (l + r) >> 1; 46 build(lson, l, mid), build(rson, mid + 1, r); 47 push_up(i); 48 return ; 49 } 50 void add(int i, int l, int r, int L, int R, int k){ 51 if(L <= l && r <= R) { 52 tree[i].sum = k; 53 tree[i].max = k; 54 return ; 55 } 56 if(l > R || r < L) return ; 57 int mid = (l + r) >> 1; 58 if(L <= mid) add(lson, l, mid, L, R, k); 59 if(R > mid) add(rson, mid + 1, r, L, R, k); 60 push_up(i); 61 return ; 62 } 63 int get_sum(int i, int l, int r, int L, int R){ 64 int sum = 0; 65 if(L <= l && r <= R) { 66 return tree[i].sum; 67 } 68 if(l > R || r < L) return 0; 69 int mid = (l + r) >> 1; 70 if(mid >= L) sum += get_sum(lson, l, mid, L, R); 71 if(mid < R) sum += get_sum(rson, mid + 1, r, L, R); 72 return sum; 73 } 74 int get_max(int i, int l, int r, int L, int R){ 75 int maxm = inf; 76 if(L <= l && r <= R){ 77 return tree[i].max; 78 } 79 if(l > R || r < L) return inf; 80 int mid = (l + r) >> 1; 81 if(mid >= L) maxm = max (maxm, get_max(lson, l, mid, L, R)); 82 if(mid < R) maxm = max (maxm, get_max(rson, mid + 1, r, L, R)); 83 return maxm; 84 } 85 } 86 87 namespace Cut{ 88 int num_edge = 0, cnt = 0, head[MAXN << 1] = {0}; 89 struct edge{ 90 int nxt, to, from; 91 }e[MAXN << 1]; 92 void add(int from, int to){ 93 e[++num_edge].to = to; 94 e[num_edge].from = from; 95 e[num_edge].nxt = head[from]; 96 head[from] = num_edge; 97 } 98 void dfs(int x, int fa){// 99 siz[x] = 1, fath[x] = fa, dep[x] = dep[fa] + 1; 100 for(int i = head[x]; i; i = e[i].nxt){ 101 int v = e[i].to; 102 if(v == fa) continue; 103 dfs(v, x); 104 siz[x] += siz[v]; 105 if(siz[son[x]] < siz[v]) son[x] = v; 106 } 107 } 108 void dfs2(int x, int tp){ 109 top[x] = tp, dfn[x] = ++cnt, pre[cnt] = x; 110 if(son[x]) dfs2(son[x], tp); 111 for(int i = head[x]; i; i = e[i].nxt){ 112 int v = e[i].to; 113 if(v == fath[x] || son[x] == v) continue; 114 dfs2(v, v); 115 } 116 } 117 int ask_sum(int x, int y){ 118 int ans = 0; 119 while(top[x] != top[y]){ 120 if(dep[top[x]] < dep[top[y]]) swap(x, y); 121 ans += Seg::get_sum(1, 1, n, dfn[top[x]], dfn[x]); 122 x = fath[top[x]]; 123 } 124 if(dfn[x] > dfn[y]) swap(x, y); 125 ans += Seg::get_sum(1, 1, n, dfn[x], dfn[y]); 126 return ans; 127 } 128 int ask_max(int x, int y){ 129 int maxm = inf; 130 while(top[x] != top[y]){ 131 if(dep[top[x]] < dep[top[y]]) swap(x, y); 132 maxm = max (maxm, Seg::get_max(1, 1, n, dfn[top[x]], dfn[x])); 133 x = fath[top[x]]; 134 } 135 if(dfn[x] > dfn[y]) swap(x, y); 136 maxm = max (maxm, Seg::get_max(1, 1, n, dfn[x], dfn[y])); 137 return maxm; 138 } 139 } 140 141 signed main() 142 { 143 n = read(); 144 for(int i = 1, u, v; i <= n - 1; ++i) { 145 u = read(), v = read(); 146 Cut::add(u, v), Cut::add(v, u); 147 } 148 for(int i = 1; i <= n; ++i) a[i] = read(); 149 150 Cut::dfs(1,0), Cut::dfs2(1, 1), Seg::build(1, 1, n); 151 152 m = read(); 153 for(int i = 1, x, y, k; i <= m; ++i){ 154 cin>>s; 155 if(s[1] == 'M'){//Qmax 156 x = read(), y = read(); 157 if(x > y) swap(x, y); 158 printf("%lld\n", Cut::ask_max(x, y)); 159 } 160 if(s[1] == 'H'){//Change 161 x = read(), k = read(); 162 Seg::add(1, 1, n, dfn[x], dfn[x], k); 163 } 164 if(s[1] == 'S'){//Qsum 165 x = read(), y = read(); 166 if(x > y) swap(x, y); 167 printf("%lld\n", Cut::ask_sum(x, y)); 168 } 169 } 170 return 0; 171 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号