Bzoj3772 精神污染

Time Limit: 10 Sec  Memory Limit: 64 MB
Submit: 446  Solved: 129

Description

兵库县位于日本列岛的中央位置，北临日本海，南面濑户内海直通太平洋，中央部位是森林和山地，与拥有关西机场的大阪府比邻而居，是关西地区面积最大的县，是集经济和文化于一体的一大地区，是日本西部门户，海陆空交通设施发达。濑户内海沿岸气候温暖，多晴天，有日本少见的贸易良港神户港所在的神户市和曾是豪族城邑“城下町”的姬路市等大城市，还有以疗养地而闻名的六甲山地等。
兵库县官方也大力发展旅游，为了方便，他们在县内的N个旅游景点上建立了n-1条观光道，构成了一棵图论中的树。同时他们推出了M条观光线路，每条线路由两个节点x和y指定，经过的旅游景点就是树上x到y的唯一路径上的点。保证一条路径只出现一次。
你和你的朋友打算前往兵库县旅游，但旅行社还没有告知你们最终选择的观光线路是哪一条（假设是线路A）。这时候你得到了一个消息：在兵库北有一群丧心病狂的香菜蜜，他们已经选定了一条观光线路（假设是线路B），对这条路线上的所有景点都释放了【精神污染】。这个计划还有可能影响其他的线路，比如有四个景点1-2-3-4，而【精神污染】的路径是1-4，那么1-3,2-4,1-2等路径也被视为被完全污染了。
现在你想知道的是，假设随便选择两条不同的路径A和B，存在一条路径使得如果这条路径被污染，另一条路径也被污染的概率。换句话说，一条路径被另一条路径包含的概率。
 

 

Input

第一行两个整数N,M
接下来N-1行，每行两个数a,b，表示A和B之间有一条观光道。
接下来M行，每行两个数x,y，表示一条旅游线路。
 

 

Output

所求的概率，以最简分数形式输出。
 

 

Sample Input

5 3
1 2
2 3
3 4
2 5
3 5
2 5
1 4

Sample Output

1/3
样例解释
可以选择的路径对有(1,2),(1,3),(2,3)，只有路径1完全覆盖路径2。

HINT

 

100%的数据满足：N,M<=100000

 

Source

 

辣鸡破题耗我时间颓我青春

 

解法一：dfs序+主席树

“如果路径A包含于路径B 那么就有A的两端点在路径B上”

主席树以dfs序为“时间轴”维护dfs序区间上的信息（可持久化树树？）

树上的主席树和序列上的主席树差不多一个意思，只是提取区间时候从root[后]-root[前]变成了root[x]-root[LCA]

搞出树的DFS序，对于每条链(x,y)，在x的dfs序位置差分标记y的子树区间。查询每条链(x,y)时，利用主席树提取出(x,LCA(x,y))和(y,LCA(x,y))这两段链上面的标记，就可以知道有多少链被当前的链包含。

每条链统计答案的时候要减去自己。

概率就是有污染的道路对的数量除以全部道路对的数量。

我猜没人能看懂上面说了啥，还是左转popoQQQ大爷的讲解吧http://blog.csdn.net/PoPoQQQ/article/details/43122821

破题卡内存丧心病狂。内存计算经验不足（你根本就懒得算吧喂），卡了一页MLE。

真是对不起学姐号的AC率啊。

  1 /*by SilverN*/
  2 #include<iostream>
  3 #include<algorithm>
  4 #include<cstring>
  5 #include<cstdio>
  6 #include<cmath>
  7 #include<vector>
  8 #define LL long long
  9 using namespace std;
 10 const int mxn=100005;
 11 int read(){
 12     int x=0,f=1;char ch=getchar();
 13     while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();}
 14     while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();}
 15     return x*f;
 16 }
 17 struct edge{
 18     int v,nxt;
 19 }e[mxn<<1];
 20 int hd[mxn],mct=0;
 21 void add_edge(int u,int v){
 22     e[++mct].v=v;e[mct].nxt=hd[u];hd[u]=mct;return;
 23 }
 24 //
 25 int fa[mxn],sz[mxn],top[mxn],son[mxn];
 26 int ind[mxn],out[mxn],dtime=0;
 27 int dep[mxn];
 28 void DFS1(int u){
 29     dep[u]=dep[fa[u]]+1;
 30     sz[u]=1;
 31     for(int i=hd[u];i;i=e[i].nxt){
 32         if(e[i].v==fa[u])continue;
 33         fa[e[i].v]=u;
 34         DFS1(e[i].v);
 35         sz[u]+=sz[e[i].v];
 36         if(sz[e[i].v]>sz[son[u]])son[u]=e[i].v;
 37     }
 38     return;
 39 }
 40 void DFS2(int u,int tp){
 41     ind[u]=++dtime;
 42     top[u]=tp;
 43     if(son[u]){
 44         DFS2(son[u],tp);
 45         for(int i=hd[u];i;i=e[i].nxt)
 46             if(e[i].v!=fa[u] && e[i].v!=son[u])DFS2(e[i].v,e[i].v);
 47     }
 48     out[u]=++dtime;
 49     return;
 50 }
 51 int LCA(int x,int y){
 52     while(top[x]!=top[y]){
 53         if(dep[top[x]]<dep[top[y]])swap(x,y);
 54         x=fa[top[x]];
 55     }
 56     return dep[x]<dep[y]?x:y;
 57 }
 58 //
 59 vector<int>ch[mxn];
 60 struct node{
 61     int l,r;
 62     int smm;
 63 }t[mxn*40];
 64 int rot[mxn*8],sct=0;
 65 void insert(int p,short v,int l,int r,int y,int &rt){
 66     rt=++sct;
 67     t[rt]=t[y];
 68     if(l==r){t[rt].smm+=v;return;}
 69     int mid=(l+r)>>1;
 70     if(p<=mid) insert(p,v,l,mid,t[y].l,t[rt].l);
 71     else insert(p,v,mid+1,r,t[y].r,t[rt].r);
 72     t[rt].smm=t[t[rt].l].smm+t[t[rt].r].smm;
 73     return;
 74 }
 75 int query(int L,int R,int l,int r,int R1,int R2,int R3,int R4){
 76     if(L<=l && r<=R){
 77         return t[R1].smm-t[R3].smm-t[R4].smm+t[R2].smm;
 78         //左端点+右端点-LCA-LCA以上的链 
 79     }
 80     int mid=(l+r)>>1;
 81     int res=0;
 82     if(L<=mid)res+=query(L,R,l,mid,t[R1].l,t[R2].l,t[R3].l,t[R4].l);
 83     if(R>mid)res+=query(L,R,mid+1,r,t[R1].r,t[R2].r,t[R3].r,t[R4].r);
 84     return res;
 85 }
 86 int n,m,ed;
 87 void DFS3(int u){
 88     int tmp=rot[u];
 89     rot[u]=rot[fa[u]];
 90     for(int i=0;i<ch[u].size();i++){
 91         int v=ch[u][i];
 92         insert(ind[v],1,1,ed,rot[u],tmp);
 93         rot[u]=tmp;
 94         insert(out[v],-1,1,ed,rot[u],tmp);
 95         rot[u]=tmp;
 96     }
 97     for(int i=hd[u];i;i=e[i].nxt){
 98         if(e[i].v==fa[u])continue;
 99         DFS3(e[i].v);
100     }
101     return;
102 }
103 //
104 struct mach{
105     int x,y;
106     bool operator < (const mach &b)const{
107         return (x==b.x && y<b.y)||(x<b.x);
108     }
109 }a[mxn];
110 LL gcd(LL a,LL b){return (!b)?a:gcd(b,a%b);}
111 int main(){
112     int i,j,u,v;
113     n=read();m=read();
114     for(i=1;i<n;i++){
115         u=read();v=read();
116         add_edge(u,v);add_edge(v,u);
117     }
118     DFS1(1);DFS2(1,1);
119     for(i=1;i<=m;i++){
120         a[i].x=read();a[i].y=read();
121         ch[a[i].x].push_back(a[i].y);
122     }
123     ed=dtime;
124     sort(a+1,a+m+1);
125     DFS3(1);
126     LL up=0,down=(LL)m*(m-1)/2;
127     for(i=1;i<=m;i++){
128         int x=a[i].x,y=a[i].y;
129         int tmp=LCA(x,y);
130         up+=query(ind[tmp],ind[x],1,ed,rot[x],rot[y],rot[tmp],rot[fa[tmp]]);
131         up+=query(ind[tmp],ind[y],1,ed,rot[x],rot[y],rot[tmp],rot[fa[tmp]]);
132         up-=query(ind[tmp],ind[tmp],1,ed,rot[x],rot[y],rot[tmp],rot[fa[tmp]]);
133         --up;//不包含自身 
134     }
135     for(i=1;i<=m;i++)
136         for(j=i;j<=m && a[j].x==a[i].x && a[j].y==a[i].y;j++){
137             up-=(LL)(j-i)*(j-i-1)/2;
138         }
139     LL tmp=gcd(up,down);
140     up/=tmp;down/=tmp;
141     printf("%lld/%lld\n",up,down);
142     return 0;
143 }
一

 

解法二：dfs序+扫描线

我猜这个肯定是出题人想的正解，毕竟这么写不会被卡内存

链的包含无非两种情况：

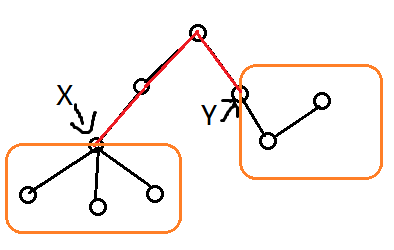
如果链长成这样，如果一条链包含了(x,y)，那么它的起点肯定在x的子树里，终点肯定在y的子树里（起终点可以反过来）

 

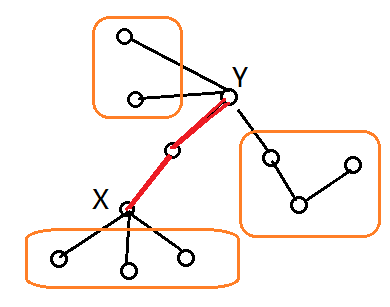
如果链长成这样，如果一条链包含了(x,y)，那么它的一端肯定在x的子树内，另一端在y除了x所在子树以外的其他任意子树内。

“y的通向x所在子树的子结点”这个可以用和LCA相同的方法找到

 

让我们看看可以怎么利用这个性质：

如果一条链(x,y)被别的链包含，那么它的起点一定在对应的dfs序区间内，终点也一定在对应的dfs序区间内。

把起点区间看成x轴，终点区间看成y轴，问题转化成了——对于每个点对(dfn[x],dfn[y])，查找有多少覆盖了它的矩形。

扫描线大法好

  1 /*by SilverN*/
  2 #include<iostream>
  3 #include<algorithm>
  4 #include<cstring>
  5 #include<cstdio>
  6 #include<cmath>
  7 #include<vector>
  8 #define LL long long
  9 using namespace std;
 10 const int mxn=120010;
 11 int read(){
 12     int x=0,f=1;char ch=getchar();
 13     while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();}
 14     while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();}
 15     return x*f;
 16 }
 17 struct edge{
 18     int v,nxt;
 19 }e[mxn<<1];
 20 int hd[mxn],mct=0;
 21 void add_edge(int u,int v){
 22     e[++mct].v=v;e[mct].nxt=hd[u];hd[u]=mct;return;
 23 }
 24 //
 25 struct Line{
 26     int x,y1,y2,tp;
 27     bool operator < (const Line &b)const{return x<b.x;}
 28 }line[mxn*6];
 29 int lct=0;
 30 void addline(int x1,int x2,int y1,int y2){
 31     if(y1>y2)return;
 32     line[++lct]=(Line){x1,y1,y2,1};
 33     line[++lct]=(Line){x2+1,y1,y2,-1};
 34     line[++lct]=(Line){y1,x1,x2,1};
 35     line[++lct]=(Line){y2+1,x1,x2,-1};
 36     return;
 37 }
 38 int fa[mxn][19];
 39 int ind[mxn],out[mxn],dep[mxn],dtime=0;
 40 void DFS1(int u,int ff){
 41     ind[u]=++dtime;
 42     dep[u]=dep[ff]+1;
 43     for(int i=1;i<19;i++)fa[u][i]=fa[fa[u][i-1]][i-1];
 44     for(int i=hd[u],v;i;i=e[i].nxt){
 45         v=e[i].v;
 46         if(v==ff)continue;
 47         fa[v][0]=u;
 48         DFS1(v,u);
 49     }
 50     out[u]=dtime;
 51     return;
 52 }
 53 int LCA_second(int x,int y){
 54     if(dep[x]<dep[y])swap(x,y);
 55     for(int i=18;i>=0;i--)
 56         if(dep[fa[x][i]]>dep[y])x=fa[x][i];
 57     return x;
 58 }
 59 //
 60 struct node{int smm;}t[mxn<<2];
 61 #define ls rt<<1
 62 #define rs rt<<1|1
 63 void update(int L,int R,int v,int l,int r,int rt){
 64     if(L<=l && r<=R){t[rt].smm+=v;return;}
 65     int mid=(l+r)>>1;
 66     if(L<=mid)update(L,R,v,l,mid,ls);
 67     if(R>mid)update(L,R,v,mid+1,r,rs);
 68     return;
 69 }
 70 int query(int p,int l,int r,int rt){
 71     if(l==r)return t[rt].smm;
 72     int mid=(l+r)>>1;
 73     if(p<=mid)return t[rt].smm+query(p,l,mid,ls);
 74     else return t[rt].smm+query(p,mid+1,r,rs);
 75 }
 76 #undef ls
 77 #undef rs
 78 //
 79 struct Query{
 80     int x,y;
 81     bool operator < (const Query &b)const{
 82         return (x==b.x && y<b.y)||(x<b.x);
 83     }
 84 }q[mxn];
 85 int n,m;
 86 LL gcd(LL a,LL b){return (!b)?a:gcd(b,a%b);}
 87 int main(){
 88     int i,j,u,v;
 89     n=read();m=read();
 90     for(i=1;i<n;i++){
 91         u=read();v=read();
 92         add_edge(u,v);
 93         add_edge(v,u);
 94     }
 95     DFS1(1,0);
 96     int x,y;
 97     bool flag=0;
 98     for(i=1;i<=m;i++){
 99         x=read();y=read();
100         if(dep[x]>dep[y])swap(x,y);
101         q[i].x=ind[x];q[i].y=ind[y];
102         if(x==y){
103             addline(ind[y],out[y],1,ind[y]);
104             addline(ind[y],out[y],out[y]+1,n);
105             continue;
106         }
107         if(ind[x]<=ind[y] && out[y]<=out[x]){//y在x的子树中 
108             int tmp=LCA_second(x,y);
109             addline(ind[y],out[y],1,ind[tmp]-1);
110             addline(ind[y],out[y],out[tmp]+1,n);
111         }
112         else{
113             addline(ind[x],out[x],ind[y],out[y]);
114         }
115     }
116     LL up=0,down=(LL)m*(m-1)/2;
117     sort(line+1,line+lct+1);
118     sort(q+1,q+m+1);
119     int now=1;
120     for(i=1;i<=m;i++){
121         while(now<=lct && line[now].x<=q[i].x){
122             update(line[now].y1,line[now].y2,line[now].tp,1,n,1);
123             now++;
124         }
125         int tmp=query(q[i].y,1,n,1);
126         up+=tmp;
127         --up;
128     }
129     for(i=1;i<=m;i=j)
130         for(j=i;j<=m && q[i].x==q[j].x && q[i].y==q[j].y;j++){
131             up-=(LL)(j-i)*(j-i-1)/2;
132         }
133     LL tmp=gcd(up,down);
134     up/=tmp;down/=tmp;
135     printf("%lld/%lld\n",up,down);
136     return 0;
137 }

 

posted @ 2017-04-27 20:09  SilverNebula  阅读(170)  评论(0)  编辑  收藏  举报
AmazingCounters.com