HDU2481 Toy

Time Limit: 16000/8000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 661    Accepted Submission(s): 363


Problem Description
On birthday, Anthony got a toy. It is constructed with N+1(N>=3) balls and 2*N sticks. All balls are in a same plane. One of them is special, while the other N balls are connected to it by N sticks with the same length. The angles between any two adjacent sticks are equal. And finally, any two adjacent balls(except the central one) are connected by a stick.
  Here are two examples:

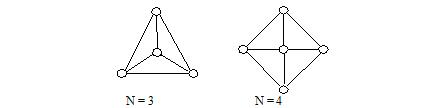
Anthony wanted to remove N sticks, leaving all balls still connected. He wanted to know the number of all legal solutions. Your task is to solve this problem for him. 
  Notice that if a solution will be the same as another one by rotation, these two solutions should be consider as the same. 
The answer may be quite large. You just need to calculate the remainder of the answer when divided by M.
 

 

Input
Input contains several test cases. 
For each test case, there is only one line containing two integers N and M(3<=N<=10^9, 2<=M<=10^9). 
Input is terminated by EOF.
 

 

Output
For each case, output one integer in one line, representing the remainder of the number of all solutions when divided by M.

 

 

Sample Input
3 10000 4 10000 4 10
 

 

Sample Output
6 13 3
 

 

Source
2008 Asia Regional Chengdu
 

 

Recommend
lcy

 

突然想起MH四baka

 

数学问题 递推 矩阵加速 快速乘 置换群 burnside引理 欧拉函数

考点真全，真带感

前置技能 本题要用的递推式 Bzoj1002 [FJOI2007]轮状病毒

　　　　 置换群 旋转同构计数 POJ2154 Color

　　　　 快速乘 HDU5187 zhx's contest

 

可以发现这题要求的生成树和轮状病毒那题一样，可以用同一个递推式子。

由于n很大，不能直接递推，需要矩阵乘法优化。

然后在外面套一个burnside引理即可。

由于M不一定是质数，不能求逆元，为了保证除法正确性，需要在mod （n*M）的意义下计算，才可以/n

(n*M)的范围是1e18，这使得普通乘法会爆LL，需要加一个快速乘优化。

快速乘不支持乘负数的样子，所以把递推矩阵里的-1加到mod-1，在模意义下等价 

 

理清思路以后就是按模块把代码堆上去，写起来挺爽的。

namespace没什么卵用，但是莫名帅啊

  1 #include<iostream>
  2 #include<algorithm>
  3 #include<cstring>
  4 #include<cstdio>
  5 #include<cmath>
  6 #define LL long long
  7 using namespace std;
  8 const int mxn=100010;
  9 int read(){
 10     int x=0,f=1;char ch=getchar();
 11     while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();}
 12     while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();}
 13     return x*f;
 14 }
 15 LL mod;
 16 namespace Euler{
 17     int pri[mxn],cnt=0;
 18     bool vis[mxn];
 19     void init(){
 20         for(int i=2;i<mxn;i++){
 21             if(!vis[i])
 22                 pri[++cnt]=i;
 23             for(int j=1;j<=cnt && (LL)pri[j]*i<mxn;j++){
 24                 vis[pri[j]*i]=1;
 25                 if(i%pri[j]==0)break;
 26             }
 27         }
 28         return;
 29     }
 30     LL phi(LL x){
 31         LL res=x;
 32         for(int i=1;i<=cnt && pri[i]<=x;i++){
 33             if(x%pri[i]==0){
 34                 res=res/pri[i]*(pri[i]-1);
 35                 while(x%pri[i]==0)x/=pri[i];
 36             }
 37         }
 38         if(x>1)res=res/x*(x-1);
 39         return res%mod;
 40     }
 41 }
 42 int n,M;
 43 LL f1,f2;
 44 LL ksmul(LL a,LL k){
 45     LL res=0;
 46 //    printf("ksmul:%lld %lld\n",a,k);
 47     while(k){
 48         if(k&1)res+=a;  if(res>=mod)res-=mod;
 49         a<<=1;    if(a>=mod)a-=mod;
 50         k>>=1;
 51     }
 52 //    printf("d\n");
 53     return res;
 54 }
 55 struct Mat{
 56     LL x[4][4];
 57     Mat operator * (Mat b){
 58         Mat res;
 59         for(int i=1;i<=3;i++)
 60             for(int j=1;j<=3;j++){
 61                 res.x[i][j]=0;
 62                 for(int k=1;k<=3;k++){
 63                     (res.x[i][j]+=ksmul(x[i][k],b.x[k][j]))%=mod;
 64 //                    printf("i:%d j:%d k:%d\n",i,j,k);
 65                 }
 66             }
 67         return res;
 68     }
 69     void init(){
 70         memset(x,0,sizeof x);
 71         x[1][1]=5;
 72         x[1][2]=1;
 73         x[1][3]=2;
 74         return;
 75     }
 76 }mp,now;
 77 void ksm(Mat a,LL k){
 78     now.init();
 79     while(k){
 80         if(k&1)now=now*a;
 81         a=a*a;
 82         k>>=1;
 83     }
 84     return; 
 85 }
 86 LL solve(int k){
 87     if(k==1)return 1;
 88     if(k==2)return 5;
 89 //    printf("solving %d\n",k);
 90     ksm(mp,k-1);
 91 //    printf("solved %d %lld %lld %lld\n",k,now.x[1][1],now.x[1][2],now.x[1][3]);
 92     return now.x[1][2];
 93 }
 94 int main(){
 95     using namespace Euler;
 96     int i,j;
 97     init();
 98     mp.x[1][1]=3;
 99 //    mp.x[2][1]=-1;
100     mp.x[3][1]=1;mp.x[3][3]=1;
101     mp.x[1][2]=1;
102     while(scanf("%d%d",&n,&M)!=EOF){
103         mod=(LL)n*M;
104         mp.x[2][1]=mod-1;
105         LL ans=0;
106         for(i=1;i*i<n;i++){
107             if(n%i==0){
108                 (ans+=ksmul(solve(i),phi(n/i)))%=mod;
109                 (ans+=ksmul(solve(n/i),phi(i)))%=mod;
110             }
111         }
112         if(i*i==n) (ans+=solve(i)*phi(i))%=mod;
113         ans/=n;
114         printf("%lld\n",ans);
115     }
116     return 0;
117 }

 

posted @ 2017-04-12 00:11  SilverNebula  阅读(404)  评论(0)  编辑  收藏  举报
AmazingCounters.com