Bzoj2154 Crash的数字表格

Time Limit: 20 Sec  Memory Limit: 259 MB
Submit: 3325  Solved: 1247

Description

今天的数学课上，Crash小朋友学习了最小公倍数(Least Common Multiple)。对于两个正整数a和b，LCM(a, b)表示能同时被a和b整除的最小正整数。例如，LCM(6, 8) = 24。回到家后，Crash还在想着课上学的东西，为了研究最小公倍数，他画了一张N*M的表格。每个格子里写了一个数字，其中第i行第j列的那个格子里写着数为LCM(i, j)。一个4*5的表格如下： 1 2 3 4 5 2 2 6 4 10 3 6 3 12 15 4 4 12 4 20 看着这个表格，Crash想到了很多可以思考的问题。不过他最想解决的问题却是一个十分简单的问题：这个表格中所有数的和是多少。当N和M很大时，Crash就束手无策了，因此他找到了聪明的你用程序帮他解决这个问题。由于最终结果可能会很大，Crash只想知道表格里所有数的和mod 20101009的值。

Input

输入的第一行包含两个正整数，分别表示N和M。

Output

输出一个正整数，表示表格中所有数的和mod 20101009的值。

Sample Input

4 5

Sample Output

122
【数据规模和约定】
100%的数据满足N, M ≤ 10^7。

HINT

 

Source

 

数学问题 莫比乌斯反演

 

题目要求的是这个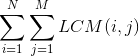：　　　　很明显也就是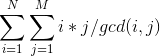　　

 

如果我们要求 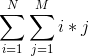 ，可以这么搞：

　　i和j都带进等差数列公式，设上式为函数sum[N,M]，则 $sum[N,M]=(N(N+1)/2)*(M(M+1)/2)$

如果要求gcd(i,j)的和，也有方便的方法：http://www.cnblogs.com/SilverNebula/p/6582843.html

当然不可以分别算上面和下面，然后两式相除，但是↑这里的分块求值方法给了我们一定启发：对于gcd(i,j)相等的一段i和j，上面除以下面满足除法分配律，是可行的。

枚举因数d=gcd(i,j)，则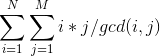可以化成 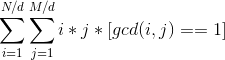 ，这个是可以求的

枚举累加过程会有重复算的部分，这时候就需要莫比乌斯函数来解决问题了

 

为了表示方便，令a=N/d,b=M/d

设，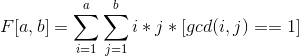

我们可以搞出

这个东西累加一下就是我们要的结果: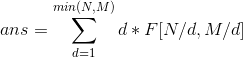

 

加上LL以后就突然各种挂，调了好久

/*by SilverN*/
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<vector>
#define LL long long
using namespace std;
const LL inv2=10050505;
const LL mod=20101009;
const int mxn=10000010;
int pri[mxn],cnt=0;
int mu[mxn];
LL smm[mxn];
bool vis[mxn];
void init(){
    mu[1]=1;
    for(int i=2;i<mxn;i++){
        if(!vis[i]){
            pri[++cnt]=i;
            mu[i]=-1;
        }
        for(int j=1;j<=cnt && (LL)pri[j]*i<mxn;j++){
            vis[i*pri[j]]=1;
            if(i%pri[j]==0){mu[i*pri[j]]=0;break;}
            mu[i*pri[j]]=-mu[i];
        }
    }
    for(int i=1;i<mxn;i++)smm[i]=(smm[i-1]+(LL)i*mu[i]*i)%mod;
    return;
}
int SUM(int x,int y){
    return ((LL)x*(x+1)%mod*inv2%mod)*((LL)y*(y+1)%mod*inv2%mod)%mod;
}
inline int s1(int x){return (x*(x+1)%mod*inv2%mod);} 
LL calc(int a,int b){
    LL res=0;int pos;
    if(a>b)swap(a,b);
    for(int i=1;i<=a;i=pos+1){
        int x=a/i,y=b/i;
        pos=min(a/x,b/y);
        res+=(smm[pos]-smm[i-1])*SUM(x,y);
        res%=mod;
    }
    return res;
}
int solve(int a,int b){
    LL res=0;int pos;
    if(a>b)swap(a,b);
    for(int i=1;i<=a;i=pos+1){
        int x=a/i,y=b/i;
        pos=min(a/x,b/y);
        (res+=(s1(pos)-s1(i-1))*calc(x,y))%=mod;
    }
    return res;
}
LL n,m;
int main(){
    int i,j;
    init();
    cin>>n>>m;
    printf("%d\n",solve(n,m));
    return 0;
}