Bzoj1101 [POI2007]Zap

Time Limit: 10 Sec  Memory Limit: 162 MB
Submit: 2414  Solved: 995
[Submit][Status][Discuss]

Description

　　FGD正在破解一段密码，他需要回答很多类似的问题：对于给定的整数a,b和d，有多少正整数对x,y，满足x<=a
，y<=b，并且gcd(x,y)=d。作为FGD的同学，FGD希望得到你的帮助。

Input

　　第一行包含一个正整数n，表示一共有n组询问。（1<=n<= 50000）接下来n行，每行表示一个询问，每行三个
正整数，分别为a,b,d。（1<=d<=a,b<=50000）

Output

　　对于每组询问，输出到输出文件zap.out一个正整数，表示满足条件的整数对数。

Sample Input

2
4 5 2
6 4 3

Sample Output

3
2
//对于第一组询问，满足条件的整数对有(2,2)，（2,4），（4，2）。对于第二组询问，满足条件的整数对有（
6,3），（3,3）。

HINT

 

Source

 

数学问题 莫比乌斯反演 分块

 

  当然可以化成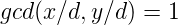 

 

所以我们要求的变成下面这个：

 

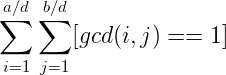
为了表示方便，重新赋值a=a/d,b=b/d

下面，d用作莫比乌斯函数的记号，与题目给出的d无关

利用莫比乌斯函数的性质把上式化成：

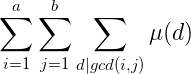
由于d|gcd(i,j)等价于 (d|i) && (d|j)

上式化成：

也就是

 

 

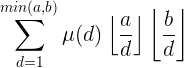
发现d取值在一个连续区间时，a/d的结果是相同的，所以可以用分块的方式，将a/d结果相同的一个区间放在一起算。

而这段区间内的μ(d)可以通过求前缀和得到

 

/*by SilverN*/
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
const int mxn=50011;
int read(){
    int x=0,f=1;char ch=getchar();
    while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int pri[mxn],cnt=0;
int mu[mxn],smm[mxn];
bool vis[mxn];
void init(){
    mu[1]=1;
    for(int i=2;i<mxn;i++){
        if(!vis[i]){pri[++cnt]=i;mu[i]=-1;}
        for(int j=1;j<=cnt && pri[j]*i<mxn;j++){
            vis[pri[j]*i]=1;
            if(i%pri[j]==0){
                mu[i*pri[j]]=0;
                break;
            }
            mu[i*pri[j]]=-mu[i];
        }
    }
    for(int i=1;i<mxn;i++)smm[i]=smm[i-1]+mu[i];
    return;
}
int clc(int n,int m){
    if(n>m)swap(n,m);
    int res=0,pos=0;
    for(int i=1;i<=n;i=pos+1){
        int x=n/i,y=m/i;
        pos=min(n/x,m/y);
        res+=(smm[pos]-smm[i-1])*x*y;
    }
    return res;
}
int main(){
    int i,j,a,b,d;
    init();
    int T=read();
    while(T--){
        a=read();b=read();d=read();
        int ans=clc(a/d,b/d);
        printf("%d\n",ans);
    }
    return 0;
}