CodeForces Round #403 (Div.2) A-F
精神不佳,选择了在场外同步划水
没想到实际做起来手感还好,早知道就报名了……
该打
未完待续233
A. Andryusha and Socks
模拟,模拟大法好。注意每次是先判断完能不能收进柜子,再算桌子上的袜子数量的。

1 /*by SilverN*/ 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<cstdio> 6 #include<cmath> 7 using namespace std; 8 const int mxn=100010; 9 int read(){ 10 int x=0,f=1;char ch=getchar(); 11 while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();} 12 while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();} 13 return x*f; 14 } 15 int a[mxn],n; 16 int cnt[mxn]; 17 int main(){ 18 int i,j,x; 19 n=read(); 20 int now=0,ans=0; 21 for(i=1;i<=n*2;i++){ 22 x=read(); 23 cnt[x]++; 24 now++; 25 if(cnt[x]==2)cnt[x]=0,now-=2; 26 ans=max(ans,now); 27 } 28 printf("%d\n",ans); 29 return 0; 30 }
B. The Meeting Place Cannot Be Changed
判能否到达,肯定是判走得最慢的那个人。
二分终点不知可不可行,我选择二分时间。在限定时间内假设所有的人都往左走,找最后一个,再假设所有人往右走,找最后一个。如果这两个“最后”可以相遇,该时间可行。
精度1e-8就T了,1e-7正合适

1 /*by SilverN*/ 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<cstdio> 6 #include<cmath> 7 using namespace std; 8 const double eps=1e-7; 9 const int mxn=100010; 10 int read(){ 11 int x=0,f=1;char ch=getchar(); 12 while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();} 13 while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();} 14 return x*f; 15 } 16 int n; 17 double ans=0; 18 double tmL[mxn],tmR[mxn]; 19 struct fri{ 20 double w,v; 21 }f[mxn]; 22 int cmp(fri a,fri b){ 23 return a.w<b.w; 24 } 25 bool solve(double lim){ 26 double ML=1000000010; 27 for(int i=1;i<=n;i++){ 28 double pos=f[i].v*lim+(double)f[i].w; 29 ML=min(ML,pos); 30 } 31 double MR=-1000000010; 32 for(int i=1;i<=n;i++){ 33 double pos=(double)f[i].w-f[i].v*lim; 34 MR=max(MR,pos); 35 } 36 if(ML-MR>=eps)return 1; 37 return 0; 38 } 39 int main(){ 40 int i,j; 41 n=read(); 42 for(i=1;i<=n;i++){ 43 f[i].w=read(); 44 } 45 for(i=1;i<=n;i++){ 46 f[i].v=read(); 47 } 48 sort(f+1,f+n+1,cmp); 49 double ans=1000000001000; 50 double l=0,r=1000000010; 51 while(r-l>=eps){ 52 double mid=(l+r)/2; 53 if(solve(mid)){ 54 ans=mid; 55 r=mid; 56 } 57 else l=mid; 58 } 59 printf("%.10lf\n",ans); 60 return 0; 61 }
C. Andryusha and Colored Balloons
直接DFS,根据父结点和当前结点已有的颜色,来判断子结点可以选什么颜色

1 /*by SilverN*/ 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<cstdio> 6 #include<cmath> 7 #include<vector> 8 #include<set> 9 using namespace std; 10 const int mxn=400010; 11 int read(){ 12 int x=0,f=1;char ch=getchar(); 13 while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();} 14 while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();} 15 return x*f; 16 } 17 struct edge{ 18 int v,nxt; 19 }e[mxn<<1]; 20 int hd[mxn],mct=0; 21 void add_edge(int u,int v){ 22 e[++mct].nxt=hd[u];e[mct].v=v;hd[u]=mct;return; 23 } 24 int n; 25 int ans[mxn]; 26 bool vis[mxn];int cnt=0; 27 void DFS(int u,int fa){ 28 int cho=1; 29 for(int i=hd[u];i;i=e[i].nxt){ 30 int v=e[i].v; 31 if(v==fa)continue; 32 while(cho==ans[u] || cho==ans[fa])cho++; 33 ans[v]=cho; 34 if(!vis[cho]){ 35 vis[cho]=1; 36 cnt++; 37 } 38 cho++; 39 DFS(v,u); 40 } 41 return; 42 } 43 int main(){ 44 int i,j,u,v; 45 n=read(); 46 for(i=1;i<n;i++){ 47 u=read();v=read(); 48 add_edge(u,v); 49 add_edge(v,u); 50 } 51 ans[1]=1;vis[1]=1;cnt++; 52 DFS(1,0); 53 printf("%d\n",cnt); 54 for(i=1;i<=n;i++){ 55 printf("%d ",ans[i]); 56 } 57 printf("\n"); 58 return 0; 59 }
D. Innokenty and a Football League
Innokenty is a president of a new football league in Byteland. The first task he should do is to assign short names to all clubs to be shown on TV next to the score. Of course, the short names should be distinct, and Innokenty wants that all short names consist of three letters.
Each club's full name consist of two words: the team's name and the hometown's name, for example, "DINAMO BYTECITY". Innokenty doesn't want to assign strange short names, so he wants to choose such short names for each club that:
- the short name is the same as three first letters of the team's name, for example, for the mentioned club it is "DIN",
- or, the first two letters of the short name should be the same as the first two letters of the team's name, while the third letter is the same as the first letter in the hometown's name. For the mentioned club it is "DIB".
Apart from this, there is a rule that if for some club x the second option of short name is chosen, then there should be no club, for which the first option is chosen which is the same as the first option for the club x. For example, if the above mentioned club has short name "DIB", then no club for which the first option is chosen can have short name equal to "DIN". However, it is possible that some club have short name "DIN", where "DI" are the first two letters of the team's name, and "N" is the first letter of hometown's name. Of course, no two teams can have the same short name.
Help Innokenty to choose a short name for each of the teams. If this is impossible, report that. If there are multiple answer, any of them will suit Innokenty. If for some team the two options of short name are equal, then Innokenty will formally think that only one of these options is chosen.
The first line contains a single integer n (1 ≤ n ≤ 1000) — the number of clubs in the league.
Each of the next n lines contains two words — the team's name and the hometown's name for some club. Both team's name and hometown's name consist of uppercase English letters and have length at least 3 and at most 20.
It it is not possible to choose short names and satisfy all constraints, print a single line "NO".
Otherwise, in the first line print "YES". Then print n lines, in each line print the chosen short name for the corresponding club. Print the clubs in the same order as they appeared in input.
If there are multiple answers, print any of them.
2
DINAMO BYTECITY
FOOTBALL MOSCOW
YES
DIN
FOO
2
DINAMO BYTECITY
DINAMO BITECITY
NO
3
PLAYFOOTBALL MOSCOW
PLAYVOLLEYBALL SPB
GOGO TECHNOCUP
YES
PLM
PLS
GOG
3
ABC DEF
ABC EFG
ABD OOO
YES
ABD
ABE
ABO
In the first sample Innokenty can choose first option for both clubs.
In the second example it is not possible to choose short names, because it is not possible that one club has first option, and the other has second option if the first options are equal for both clubs.
In the third example Innokenty can choose the second options for the first two clubs, and the first option for the third club.
In the fourth example note that it is possible that the chosen short name for some club x is the same as the first option of another club yif the first options of x and y are different.
暴力+二分图匹配
脑补了网络流等各种奇怪的方法,然而没有什么头绪。
再看看数据范围,啊,暴力你好,网络流再见
首先O(N^2)找出所有按照第一种编码会冲突的队伍,强制它们使用第二种编码,且不可改变。
然后依次判断每支队伍选择的编码方式,这里用到类似匈牙利算法的调整方式,如果当前决策和之前的冲突,尝试DFS向前调整,如果没有可行方案就判NO

1 /*by SilverN*/ 2 #include<iostream> 3 #include<algorithm> 4 #include<cstring> 5 #include<cstdio> 6 #include<cmath> 7 #include<queue> 8 #include<map> 9 using namespace std; 10 const int INF=1e9; 11 const int mxn=100010; 12 int read(){ 13 int x=0,f=1;char ch=getchar(); 14 while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();} 15 while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();} 16 return x*f; 17 } 18 map<string,int>mp; 19 string s1[1010],s2[1010]; 20 int vis[mxn]; 21 int cho[mxn]; 22 int n,cnt; 23 int link[mxn]; 24 bool DFS(int p){ 25 if(cho[p]!=2 && !vis[mp[s1[p]]]){ 26 vis[mp[s1[p]]]=1; 27 if(!link[mp[s1[p]]] || DFS(link[mp[s1[p]]])){ 28 link[mp[s1[p]]]=p; 29 cho[p]=1; 30 return 1; 31 } 32 } 33 if(!vis[mp[s2[p]]]){ 34 vis[mp[s2[p]]]=1; 35 if(!link[mp[s2[p]]] || DFS(link[mp[s2[p]]])){ 36 link[mp[s2[p]]]=p; 37 cho[p]=2; 38 return 1; 39 } 40 } 41 return 0; 42 } 43 int main(){ 44 n=read(); 45 int i,j; 46 for(i=1;i<=n;i++){ 47 cin>>s1[i]>>s2[i]; 48 s1[i]=s1[i].substr(0,3); 49 s2[i]=s1[i].substr(0,2)+s2[i].substr(0,1); 50 if(!mp[s1[i]])mp[s1[i]]=++cnt; 51 if(!mp[s2[i]])mp[s2[i]]=++cnt; 52 } 53 for(i=1;i<=n;i++){ 54 memset(vis,0,sizeof vis); 55 for(j=1;j<=n;j++){ 56 if(i==j)continue; 57 if(s1[i]==s1[j]){ 58 cho[i]=2;break; 59 } 60 } 61 if(!DFS(i)){ 62 printf("NO\n"); 63 return 0; 64 } 65 } 66 printf("YES\n"); 67 for(i=1;i<=n;i++){ 68 if(cho[i]==2){ 69 cout<<s2[i]<<endl; 70 } 71 else cout<<s1[i]<<endl; 72 } 73 return 0; 74 }
E. Underground Lab
DFS序 脑洞题
吼题,吼题。刚开始毫无头绪,然后注意到每个人可以走2n/k个结点。←也就是说,每个结点走两遍都足够了。
那么先找出图的生成树,然后处理出DFS序,让每个人按DFS序能走多远走多远,达到限制就再换一个人走,就可以了。
注意这种贪心法可能用不完所有的人就出解了,但实际上要输出所有人的行走方案。因为没有注意到这个,一直WA 7。
↑解决方案是让没有用到的人都输出1 1(待在原地)

1 /*by SilverN*/ 2 #include<algorithm> 3 #include<iostream> 4 #include<cstring> 5 #include<cstdio> 6 #include<cmath> 7 #include<vector> 8 using namespace std; 9 const int mxn=600010; 10 int read(){ 11 int x=0,f=1;char ch=getchar(); 12 while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();} 13 while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();} 14 return x*f; 15 } 16 struct edge{ 17 int v,nxt; 18 }e[mxn]; 19 int hd[mxn],mct=0; 20 void add_edge(int u,int v){ 21 e[++mct].v=v;e[mct].nxt=hd[u];hd[u]=mct;return; 22 } 23 int n,m,k,lim; 24 int ans[mxn],cnt=0; 25 vector<int>ve[mxn]; 26 int fa[mxn]; 27 int find(int x){ 28 return fa[x]==x?x:fa[x]=find(fa[x]); 29 } 30 inline void upd(int u){ 31 if(ans[cnt]<lim){ 32 ans[cnt]++; 33 ve[cnt].push_back(u); 34 } 35 else{ 36 ++cnt;ans[cnt]++; 37 ve[cnt].push_back(u); 38 } 39 return; 40 } 41 void DFS(int u,int ff){ 42 for(int i=hd[u];i;i=e[i].nxt){ 43 int v=e[i].v; 44 if(v==ff)continue; 45 upd(u); 46 DFS(v,u); 47 } 48 upd(u); 49 return; 50 } 51 int main(){ 52 int i,j,u,v; 53 n=read();m=read();k=read(); 54 lim=(2*n+k-1)/k; 55 for(i=1;i<=n;i++)fa[i]=i; 56 for(i=1;i<=m;i++){ 57 u=read();v=read(); 58 int fu=find(u),fv=find(v); 59 if(fu!=fv){ 60 add_edge(u,v); 61 add_edge(v,u); 62 fa[fu]=fv; 63 } 64 } 65 cnt=1; 66 DFS(1,0); 67 for(i=1;i<=k;i++){ 68 if(!ans[i]){ 69 printf("1 1\n"); 70 continue; 71 } 72 printf("%d ",ans[i]); 73 for(j=0;j<ve[i].size();j++){ 74 printf("%d ",ve[i][j]); 75 } 76 printf("\n"); 77 } 78 return 0; 79 }
F. Axel and Marston in Bitland
A couple of friends, Axel and Marston are travelling across the country of Bitland. There are n towns in Bitland, with some pairs of towns connected by one-directional roads. Each road in Bitland is either a pedestrian road or a bike road. There can be multiple roads between any pair of towns, and may even be a road from a town to itself. However, no pair of roads shares the starting and the destination towns along with their types simultaneously.
The friends are now located in the town 1 and are planning the travel route. Axel enjoys walking, while Marston prefers biking. In order to choose a route diverse and equally interesting for both friends, they have agreed upon the following procedure for choosing the road types during the travel:
- The route starts with a pedestrian route.
- Suppose that a beginning of the route is written in a string s of letters P (pedestrain road) and B (biking road). Then, the string
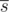 is appended to s, where
is appended to s, where 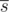 stands for the string s with each character changed to opposite (that is, all pedestrian roads changed to bike roads, and vice versa).
stands for the string s with each character changed to opposite (that is, all pedestrian roads changed to bike roads, and vice versa).
In the first few steps the route will look as follows: P, PB, PBBP, PBBPBPPB, PBBPBPPBBPPBPBBP, and so on.
After that the friends start travelling from the town 1 via Bitlandian roads, choosing the next road according to the next character of their route type each time. If it is impossible to choose the next road, the friends terminate their travel and fly home instead.
Help the friends to find the longest possible route that can be travelled along roads of Bitland according to the road types choosing procedure described above. If there is such a route with more than 1018 roads in it, print -1 instead.
The first line contains two integers n and m (1 ≤ n ≤ 500, 0 ≤ m ≤ 2n2) — the number of towns and roads in Bitland respectively.
Next m lines describe the roads. i-th of these lines contains three integers vi, ui and ti (1 ≤ vi, ui ≤ n, 0 ≤ ti ≤ 1), where vi and uidenote start and destination towns indices of the i-th road, and ti decribes the type of i-th road (0 for a pedestrian road, 1 for a bike road). It is guaranteed that for each pair of distinct indices i, j such that 1 ≤ i, j ≤ m, either vi ≠ vj, or ui ≠ uj, or ti ≠ tj holds.
If it is possible to find a route with length strictly greater than 1018, print -1. Otherwise, print the maximum length of a suitable path.
2 2
1 2 0
2 2 1
3
2 3
1 2 0
2 2 1
2 2 0
-1
In the first sample we can obtain a route of length 3 by travelling along the road 1 from town 1 to town 2, and then following the road 2 twice from town 2 to itself.
In the second sample we can obtain an arbitrarily long route by travelling the road 1 first, and then choosing road 2 or 3 depending on the necessary type.
倍增 位运算 bitset
博主当然会做这种题啦,只要用心思考很快就能得出解法了。
——可是听说博主的代码是从standings榜上rank4那里抄来的,连变量名都没怎么改就贴到博客上了呢
——啊啊啊啊啊啊啊啊啊啊读书人的事,怎么能算抄呢……是学习……学习!
(好像有点熟悉)
用bitset存储状态,倍增以u为起点走2^k步可以到哪些点。
处理完状态以后,从2^61开始倒着贪心。
1 /*by SilverN*/ 2 #include<algorithm> 3 #include<iostream> 4 #include<cstring> 5 #include<cstdio> 6 #include<cmath> 7 #include<vector> 8 #include<bitset> 9 using namespace std; 10 const int mxn=510; 11 int read(){ 12 int x=0,f=1;char ch=getchar(); 13 while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();} 14 while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();} 15 return x*f; 16 } 17 bitset<502>f[2][65][mxn];//类型 倍增长度 起始点=终点 18 bitset<502>p,q; 19 int n,m; 20 int main(){ 21 int i,j,u,v,w; 22 n=read();m=read(); 23 for(i=1;i<=m;i++){ 24 u=read();v=read();w=read(); 25 --u;--v; 26 f[w][0][u][v]=1; 27 } 28 for(int k=1;k<62;k++){ 29 for(i=0;i<n;i++){ 30 for(j=0;j<n;j++){ 31 if(f[0][k-1][i][j])f[0][k][i]|=f[1][k-1][j]; 32 if(f[1][k-1][i][j])f[1][k][i]|=f[0][k-1][j]; 33 } 34 } 35 } 36 for(i=0;i<n;i++) 37 if(f[0][61][0][i]){ 38 printf("-1\n");return 0; 39 } 40 bool tp=0; 41 long long ans=0; 42 p[0]=1; 43 for(int k=61;k>=0;k--){ 44 for(i=0;i<n;i++)q[i]=0; 45 for(j=0;j<n;j++)if(p[j]) q|=f[tp][k][j]; 46 if(q.any()){ 47 tp^=1; 48 ans+=(1LL<<k); 49 p=q; 50 } 51 } 52 if(ans>1e18)ans=-1; 53 printf("%I64d\n",ans); 54 return 0; 55 }


 vertices before the lab explodes.
vertices before the lab explodes.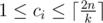 ) — the number of vertices visited by
) — the number of vertices visited by 
 浙公网安备 33010602011771号
浙公网安备 33010602011771号