POJ2699 The Maximum Number of Strong Kings
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 2102 | Accepted: 975 |
Description
A tournament can be represented by a complete graph in which each vertex denotes a player and a directed edge is from vertex x to vertex y if player x beats player y. For a player x in a tournament T, the score of x is the number of players beaten by x. The score sequence of T, denoted by S(T) = (s1, s2, . . . , sn), is a non-decreasing list of the scores of all the players in T. It can be proved that S(T) = (s1, s2, . . . , sn) is a score sequence of T if and only if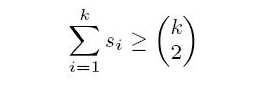
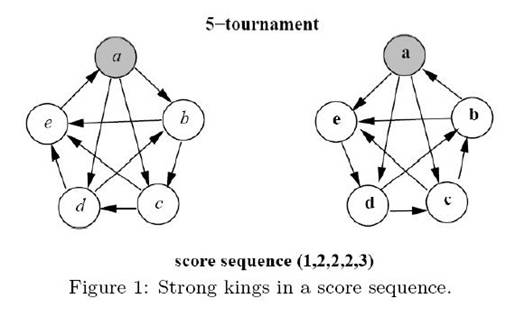
for k = 1, 2, . . . , n and equality holds when k = n. A player x in a tournament is a strong king if and only if x beats all of the players whose scores are greater than the score of x. For a score sequence S, we say that a tournament T realizes S if S(T) = S. In particular, T is a heavy tournament realizing S if T has the maximum number of strong kings among all tournaments realizing S. For example, see T2 in Figure 1. Player a is a strong king since the score of player a is the largest score in the tournament. Player b is also a strong king since player b beats player a who is the only player having a score larger than player b. However, players c, d and e are not strong kings since they do not beat all of the players having larger scores.
The purpose of this problem is to find the maximum number of strong kings in a heavy tournament after a score sequence is given. For example,Figure 1 depicts two possible tournaments on five players with the same score sequence (1, 2, 2, 2, 3). We can see that there are at most two strong kings in any tournament with the score sequence (1, 2, 2, 2, 3) since the player with score 3 can be beaten by only one other player. We can also see that T2 contains two strong kings a and b. Thus, T2 is one of heavy tournaments. However, T1 is not a heavy tournament since there is only one strong king in T1. Therefore, the answer of this example is 2.
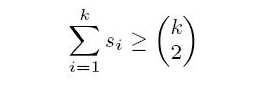
for k = 1, 2, . . . , n and equality holds when k = n. A player x in a tournament is a strong king if and only if x beats all of the players whose scores are greater than the score of x. For a score sequence S, we say that a tournament T realizes S if S(T) = S. In particular, T is a heavy tournament realizing S if T has the maximum number of strong kings among all tournaments realizing S. For example, see T2 in Figure 1. Player a is a strong king since the score of player a is the largest score in the tournament. Player b is also a strong king since player b beats player a who is the only player having a score larger than player b. However, players c, d and e are not strong kings since they do not beat all of the players having larger scores.
The purpose of this problem is to find the maximum number of strong kings in a heavy tournament after a score sequence is given. For example,Figure 1 depicts two possible tournaments on five players with the same score sequence (1, 2, 2, 2, 3). We can see that there are at most two strong kings in any tournament with the score sequence (1, 2, 2, 2, 3) since the player with score 3 can be beaten by only one other player. We can also see that T2 contains two strong kings a and b. Thus, T2 is one of heavy tournaments. However, T1 is not a heavy tournament since there is only one strong king in T1. Therefore, the answer of this example is 2.

Input
The first line of the input file contains an integer m, m <= 10, which represents the number of test cases. The following m lines contain m score sequences in which each line contains a score sequence. Note that each score sequence contains at most ten scores.
Output
The maximum number of strong kings for each test case line by line.
Sample Input
5 1 2 2 2 3 1 1 3 4 4 4 4 3 3 4 4 4 4 5 6 6 6 0 3 4 4 4 5 5 5 6 0 3 3 3 3 3
Sample Output
2 4 5 3 5
Source
网络流 最大流
将代表每场比赛的边记为流量图中的点,从S到每场比赛连边,容量为1;
从每个参赛者到T连边,容量为胜利场数。
假设king是胜场最多的前king个人,将参赛者a[]按胜利次数从大到小排序,方便连边。枚举或者二分king数量(n<=10,复杂度没啥差别),对于每场比赛,如果其中一方a是king,且另一方b胜场更多,那么将边强行定向,从比赛到a连边,容量为1(表示胜利);否则a和b都可以胜利,就将边看作双向边,比赛到a、b各连一条边,容量为1。
↑如果能跑满流,那么当前选取的king个数可行。
(测试数据格式似乎很诡异,以下代码中,如果读入方式换成注释掉的部分,本地手测都能过,交上去就WA)
刚开始有另一种设想:
将参赛者拆点,S到每个入点连边,容量为此人胜场a[i],每个出点到T连边,容量为此人负场n-1-a[i]。
枚举king的个数,每多加一个人,就在前一步的参量网络上添边,看网络流能否增广,能就继续加king人数。
但是这种算法在测discuss里的大数据时就挂掉了。
↑姑且记个思路。
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #include<queue> 6 #include<vector> 7 #define LL long long 8 using namespace std; 9 const int mx[5]={0,1,0,-1,0}; 10 const int my[5]={0,0,1,0,-1}; 11 const int mxn=300; 12 int a[mxn],n=0; 13 int cmp(const int q,const int e){return q>e;} 14 void read(){ 15 char s[210]; 16 /* fgets(s,200,stdin); 17 int len=strlen(s); 18 for(int i=0;i<len;i++){ 19 int x=0,f=1;char ch=s[i]; 20 while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=s[++i];} 21 while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=s[++i];} 22 a[++n]=x; 23 }*/ 24 gets(s); 25 int len=strlen(s); 26 for(int i=0;i<len;i++){ 27 if(s[i]>='0' && s[i]<='9')a[++n]=(s[i]-'0'); 28 } 29 return; 30 } 31 struct edge{int v,nxt,f;}e[mxn*mxn*2]; 32 int hd[mxn],mct=1; 33 inline void add_edge(int u,int v,int f){ 34 e[++mct].v=v;e[mct].f=f;e[mct].nxt=hd[u];hd[u]=mct;return; 35 } 36 inline void ins(int u,int v,int f){add_edge(u,v,f);add_edge(v,u,0);return;} 37 int S,T; 38 int id[30][30]; 39 int bct=0; 40 void init(){ 41 memset(hd,0,sizeof hd); 42 n=0;mct=1;bct=0; 43 return; 44 } 45 void init2(){ 46 for(int i=1;i<=n;i++) 47 for(int j=i+1;j<=n;j++) 48 id[i][j]=id[j][i]=++bct; 49 return; 50 } 51 int d[mxn]; 52 bool BFS(){ 53 memset(d,0,sizeof d); 54 queue<int>q; 55 d[S]=1; 56 q.push(S); 57 while(!q.empty()){ 58 int u=q.front();q.pop(); 59 for(int i=hd[u];i;i=e[i].nxt){ 60 int v=e[i].v; 61 if(!d[v] && e[i].f){ 62 d[v]=d[u]+1; 63 q.push(v); 64 } 65 } 66 } 67 return d[T]; 68 } 69 int DFS(int u,int lim){ 70 if(u==T)return lim; 71 int tmp,f=0; 72 for(int i=hd[u];i;i=e[i].nxt){ 73 int v=e[i].v; 74 if(d[v]==d[u]+1 && e[i].f){ 75 tmp=DFS(v,min(lim,e[i].f)); 76 e[i].f-=tmp; 77 e[i^1].f+=tmp; 78 f+=tmp; 79 lim-=tmp; 80 if(!lim)return f; 81 } 82 } 83 d[u]=0; 84 return f; 85 } 86 int Dinic(){ 87 int res=0; 88 while(BFS())res+=DFS(S,1e9); 89 return res; 90 } 91 int smm=0; 92 bool solve(int lim){ 93 int i,j; 94 memset(hd,0,sizeof hd); 95 mct=1; 96 for(i=1;i<=smm;i++)ins(S,i,1); 97 for(i=1;i<=n;i++)ins(smm+i,T,a[i]);//胜场 98 int hd=0; 99 for(i=1;i<=n;i++) 100 for(j=1;j<=i;j++){ 101 if(i==j)continue; 102 if(i<=lim && a[i]<a[j])ins(id[i][j],smm+i,1); 103 else{ 104 ins(id[i][j],smm+i,1); 105 ins(id[i][j],smm+j,1); 106 } 107 } 108 if(Dinic()==smm)return 1; 109 return 0; 110 } 111 int m; 112 int main() 113 { 114 scanf("%d\n",&m); 115 int i,j; 116 while(m--){ 117 init();// 118 read(); 119 sort(a+1,a+n+1,cmp); 120 init2(); 121 // for(i=1;i<=n;i++)printf("%d ",a[i]); 122 // printf("\n"); 123 smm=0; 124 for(i=1;i<=n;i++)smm+=a[i]; 125 if(smm!=n*(n-1)/2){printf("0\n");continue;} 126 smm=n*(n-1)/2; 127 S=0;T=smm+n+1; 128 int ans=0; 129 for(i=1;i<=n;i++){ 130 if(solve(i))ans=i; 131 else break; 132 } 133 printf("%d\n",ans); 134 } 135 return 0; 136 }
本文为博主原创文章,转载请注明出处。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号