洛谷P1288 取数游戏II

题目描述

有一个取数的游戏。初始时，给出一个环，环上的每条边上都有一个非负整数。这些整数中至少有一个0。然后，将一枚硬币放在环上的一个节点上。两个玩家就是以这个放硬币的节点为起点开始这个游戏，两人轮流取数，取数的规则如下：

（1）选择硬币左边或者右边的一条边，并且边上的数非0；

（2）将这条边上的数减至任意一个非负整数(至少要有所减小)；

（3）将硬币移至边的另一端。

如果轮到一个玩家走，这时硬币左右两边的边上的数值都是0，那么这个玩家就输了。

如下图，描述的是Alice和Bob两人的对弈过程，其中黑色节点表示硬币所在节点。结果图(d)中，轮到Bob走时，硬币两边的边上都是0，所以Alcie获胜。

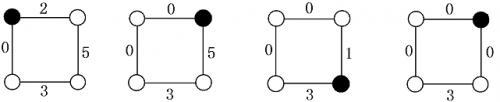
（a）Alice （b）Bob （c）Alice （d）Bob

现在，你的任务就是根据给出的环、边上的数值以及起点（硬币所在位置），判断先走方是否有必胜的策略。

输入输出格式

输入格式：

 

第一行一个整数N（N≤20），表示环上的节点数。

第二行N个数，数值不超过30，依次表示N条边上的数值。硬币的起始位置在第一条边与最后一条边之间的节点上。

 

输出格式：

 

仅一行。若存在必胜策略，则输出“YES”，否则输出“NO”。

 

输入输出样例

输入样例#1：

【输入1】
4
2 5 3 0
【输入2】
3
0 0 0

输出样例#1：

【输出1】
YES
【输出2】
NO

 

博弈论。

分析可知，走过一条边的时候不取完边上的数是没有意义的。

假设每走一条边都取完，如果从起点到0的位置有奇数条边，则先手必胜，否则后手必胜。

正着扫一遍，反着扫一遍，如果从起点到第一个遇到的0位置有奇数条边，先手必胜。

/*by SilverN*/
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<vector>
using namespace std;
const int mxn=100010;
int read(){
    int x=0,f=1;char ch=getchar();
    while(ch<'0' || ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0' && ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int n,a[mxn];
int main(){
    n=read();
    int i,j;
    for(i=1;i<=n;i++)a[i]=read();
    bool flag=1;
    for(i=1;i<=n;i++)if(!a[i]){
        if(i%2==0)flag=0;
        break;
    }
    for(i=n;i;i--)if(!a[i]){
        if((n-i+1)%2==0)flag=0;
        break;
    }
    if(flag)printf("NO\n");
    else printf("YES\n");
    return 0;
}