虚点/虚边专题
虚点/虚边专题
2019.9.18
说明:本篇文章里涉及的题目都是我在好久之前做的,有很多细节差不多忘了,只知道个大致想法,讲得不免会有些粗糙,请见谅!
所谓虚点,顾名思义,就是原本不存在的点,是由人为构建的。
水题:灌水
正如标题,此题巨水,但还算比较经典的。
题目描述
Farmer John已经决定把水灌到他的\(n(1≤n≤300)\)块农田,农田被数字\(1\)到\(n\)标记。把一块土地进行灌水有两种方法,从其他农田饮水,或者这块土地建造水库。 建造一个水库需要花费\(w_i(1≤w_i≤105)\),连接两块土地需要花费\(P_{ij}(1≤P_{ij}≤105,P_{ij}=P_{ji},P_{ii}=0)\). 计算Farmer John所需的最少代价。
输入
第一行:一个数\(n\)
第二行到第\(n+1\)行:第\(i+1\)行含有一个数\(w_i\)
第\(n+2\)行到第\(2∗n+1\)行:第\(n+1+i\)行有n个被空格分开的数,第\(j\)个数代表\(p_{ij}\)。
输出
一个单独的数代表最小代价.
样例输入
4
5
4
4
3
0 2 2 2
2 0 3 3
2 3 0 4
2 3 4 0
样例输出
9
提示
输出详解:
Farmer John在第四块土地上建立水库,然后把其他的都连向那一个,这样就要花费3+2+2+2=9
方法:虚点+最小生成树
如果把整张土地看成一张图,那么第i个点和第j个点之间的权值就是\(p_{ij}\),而要选若干条边,使所有土地都灌满水,不就是最小生成树吗?
但是还有一个问题,一个点上建立水库还需要费用,显然,我们可以枚举建立水库的点,然后跑最小生成树,这样复杂度为\(O(n^2 \cdot log(n^2))\)(边数就当作\(n^2\)条)是可以过滴。
那么,有没有更好的方法呢?
考虑到设一个源点0,那么第i个点就向源点连一条权值为\(w_i\)的边,这样不就可以照常跑最小生成树了?
复杂度\(O(n^2)\) (这里推荐用prim算法,因为克鲁斯卡尔把\(n^2\)条排序复杂度是\(o(n^2 \cdot log(n^2))\)的,不过是敲克鲁斯卡尔的)
代码:
#include<bits/stdc++.h>
using namespace std;
struct node{
int st,ed,v;
}G[100001];
int n,tot,pre[10001],done,ans;
int Find(int x){
if(pre[x]==x)return x;
return pre[x]=Find(pre[x]);
}
bool cmp(node A,node B){
return A.v<B.v;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
int a;
scanf("%d",&a);
G[++tot]=node{i,n+1,a};
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
int a;
scanf("%d",&a);
if(i>=j)continue;
G[++tot]=node{i,j,a};
}
}
sort(G+1,G+1+tot,cmp);
for(int i=1;i<=n+1;i++)pre[i]=i;
for(int i=1;i<=tot;i++){
if(done==n)break;
if(Find(G[i].st)==Find(G[i].ed))continue;
ans+=G[i].v;
pre[Find(G[i].st)]=Find(G[i].ed);
done++;
}
cout<<ans;
return 0;
}
例题1:所驼门王的宝藏
题目描述
在宽广的非洲荒漠中,生活着一群勤劳勇敢的羊驼家族。被族人恭称为“先知”的Alpaca L. Sotomon是这个家族的领袖,外人也称其为“所驼门王”。所驼门王毕生致力于维护家族的安定与和谐,他曾亲自率军粉碎河蟹帝国主义的野蛮侵略,为族人立下赫赫战功。所驼门王一生财宝无数,但因其生性节俭低调,他将财宝埋藏在自己设计的地下宫殿里,这也是今天Henry Curtis故事的起点。Henry是一个爱财如命的贪婪家伙,而又非常聪明,他费尽心机谋划了这次盗窃行动,破解重重机关后来到这座地下宫殿前。
整座宫殿呈矩阵状,由R×C间矩形宫室组成,其中有N间宫室里埋藏着宝藏,称作藏宝宫室。宫殿里外、相邻宫室间都由坚硬的实体墙阻隔,由一间宫室到达另一间只能通过所驼门王独创的移动方式——传送门。所驼门王为这N间藏宝宫室每间都架设了一扇传送门,没有宝藏的宫室不设传送门,所有的宫室传送门分为三种:
- “横天门”:由该门可以传送到同行的任一宫室;
- “纵寰门”:由该门可以传送到同列的任一宫室;
- “任意门”:由该门可以传送到以该门所在宫室为中心周围8格中任一宫室(如果目标宫室存在的话)。
深谋远虑的Henry当然事先就搞到了所驼门王当年的宫殿招标册,书册上详细记录了每扇传送门所属宫室及类型。而且,虽然宫殿内外相隔,但他自行准备了一种便携式传送门,可将自己传送到殿内任意一间宫室开始寻宝,并在任意一间宫室结束后传送出宫。整座宫殿只许进出一次,且便携门无法进行宫室之间的传送。不过好在宫室内传送门的使用没有次数限制,每间宫室也可以多次出入。
现在Henry已经打开了便携门,即将选择一间宫室进入。为得到尽多宝藏,他希望安排一条路线,使走过的不同藏宝宫室尽可能多。请你告诉Henry这条路线最多行经不同藏宝宫室的数目。
输入格式
输入文件sotomon.in第一行给出三个正整数N, R, C。
以下N行,每行给出一扇传送门的信息,包含三个正整数xi, yi, Ti,表示该传送门设在位于第xi行第yi列的藏宝宫室,类型为Ti。Ti是一个1~3间的整数,1表示可以传送到第xi行任意一列的“横天门”,2表示可以传送到任意一行第yi列的“纵寰门”,3表示可以传送到周围8格宫室的“任意门”。
保证1≤xi≤R,1≤yi≤C,所有的传送门位置互不相同。
输出格式
输出文件sotomon.out只有一个正整数,表示你确定的路线所经过不同藏宝宫室的最大数目。
输入输出样例
输入 #1
10 7 7
2 2 1
2 4 2
1 7 2
2 7 3
4 2 2
4 4 1
6 7 3
7 7 1
7 5 2
5 2 1
输出 #1
9
说明/提示
数据规模和约定:
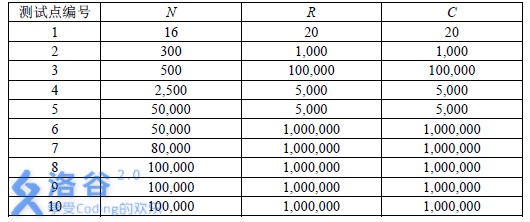
方法:虚点+Tarjan缩点+记搜
首先,如果我们把两个能互相到达的门之间连一条边,显然,这会形成一张图。
那么,我们就是要求一条路径,使其所经过的点最多。
因此,我们考虑Tarjan缩点+记搜去操作。
然鹅,你会发现,如果这样连的话,会有\(n^2\)条边,时间和空间都是承受不住的。
为此,我们考虑虚点。
我们把有门的每行和每列都开一个虚点,然后把虚点向在同行或者同列上的门连边。这样,处理横天门和纵寰门时只用连到其对应的虚点就可以了。
至于任意门的话,其最多只会和8个点连边,因此暴力连边即可。
代码:
注意:在代码实现时,我并没有加入虚点,而是把所有同一列的横天门(纵寰门也是如此)连成一个环,然后再在这一列随便选一个横天门与其它门相连。
#include<bits/stdc++.h>
#define MAXN 100010
using namespace std;
int n,R,C,mp[MAXN],mark,dfsn[MAXN],low[MAXN],cnt,bel[MAXN],size[MAXN],dp[MAXN],deg[MAXN],ans;
map<int,int> CAN[1000010];
struct node{
int num,kind,id;
}P1[MAXN],P2[MAXN];
bool cmp(node XX,node YY){
if(XX.num==YY.num){
return XX.kind<YY.kind;
}
else return XX.num<YY.num;
}
stack<int> stk;
int X[MAXN],Y[MAXN],T[MAXN];
vector<int> G[MAXN],P[MAXN];
bool in[MAXN];
map<int,bool> lian[MAXN];
int mx[]= {1,0,-1,0,1,1,-1,-1},my[]= {0,1,0,-1,1,-1,1,-1};
void Tarjan(int x) {//缩点
in[x]=true;
stk.push(x);
dfsn[x]=low[x]=++mark;
for(int i=0; i<G[x].size(); i++) {
int t=G[x][i];
if(!dfsn[t]) {
Tarjan(t);
low[x]=min(low[x],low[t]);
} else if(in[t]) {
low[x]=min(low[x],dfsn[t]);
}
}
int t;
if(dfsn[x]==low[x]) {
cnt++;
do {
t=stk.top();
stk.pop();
in[t]=false;
bel[t]=cnt;
size[cnt]++;
} while(dfsn[t]!=low[t]);
}
}
int DP(int x){//记搜
if(dp[x]!=0)return dp[x];
dp[x]=size[x];
for(int i=0;i<P[x].size();i++){
int t=P[x][i];
dp[x]=max(dp[x],DP(t)+size[x]);
}
return dp[x];
}
int main() {
scanf("%d %d %d",&n,&R,&C);
for(int i=1; i<=n; i++) {
scanf("%d %d %d",&X[i],&Y[i],&T[i]);
P1[i]=node{X[i],(T[i]!=1)+1,i};
P2[i]=node{Y[i],(T[i]!=2)+1,i};
CAN[X[i]][Y[i]]=i;
}
sort(P1+1,P1+1+n,cmp);
sort(P2+1,P2+1+n,cmp);
for(int i=1;i<=n;){
int l=i,r=i,mid=-1;
for(;P1[r+1].num==P1[l].num;r++);
if(P1[l].kind==1)for(mid=l;mid<r&&P1[mid+1].kind==1;mid++);
if(mid!=-1){
for(int j=l+1;j<=mid;j++)G[P1[j-1].id].push_back(P1[j].id);
if(mid!=l)G[P1[mid].id].push_back(P1[l].id);
for(int j=mid+1;j<=r;j++)G[P1[l].id].push_back(P1[j].id);
}
i=r+1;
}
for(int i=1;i<=n;){
int l=i,r=i,mid=-1;
for(;P2[r+1].num==P2[l].num;r++);
if(P2[l].kind==1)for(mid=l;mid<r&&P2[mid+1].kind==1;mid++);
if(mid!=-1){
for(int j=l+1;j<=mid;j++)G[P2[j-1].id].push_back(P2[j].id);
if(mid!=l)G[P2[mid].id].push_back(P2[l].id);
for(int j=mid+1;j<=r;j++)G[P2[l].id].push_back(P2[j].id);
}
i=r+1;
}
for(int i=1;i<=n;i++){
int x=X[i],y=Y[i];
if(T[i]==3){
for(int j=0;j<=8;j++){
int nex=x+mx[j],ney=y+my[j];
if(nex<1||nex>R||ney<1||ney>C)continue;
if(CAN[nex][ney]==0)continue;
G[i].push_back(CAN[nex][ney]);
}
}
}
mark=0;
for(int i=1; i<=n; i++)if(!dfsn[i])Tarjan(i);
for(int i=1;i<=n;i++){
for(int j=0;j<G[i].size();j++){
int t=G[i][j];
int st=bel[i],ed=bel[t];
if(lian[st][ed])continue;
if(st==ed)continue;
lian[st][ed]=true;
P[st].push_back(ed);
deg[ed]++;
}
}
for(int i=1;i<=cnt;i++){
if(deg[i]==0)ans=max(ans,DP(i));
}
cout<<ans;
return 0;
}
小结
通过这道题,我们可以发现虚点就像一个中枢,把许多条边先集中过来,然后再发散出去,这样大大减少了原图边的数量,起到优化时间和空间的作用。
例题2:比特镇步行
题目描述
在比特镇一共有\(n\)个街区,编号依次为\(1-n\)
比特镇的交通系统极具特色,除了\(m\)条单向道路之外,每个街区还有一个编码\(val_i\),不同街区可能拥有相同的编码。如果\(val_i\)&\(val_j=val_j\),即\(val_i\)在二进制下与\(val_j\)做与运算等于\(val_j\),那么也会存在一条额外的从i出发到j
的单向道路。Byteasar 现在位于1号街区,他想知道通过这些道路到达每一个街区最少需要多少时间。因为比特镇的交通十分发达,你可以认为通过每条道路都只需要1单位时间。
输入
第一行包含两个正整数\(n\),\(m\),表示街区的总数以及道路的总数。
第二行包含\(n\)个正整数\(val_1\),\(val_2\),...,\(val_n\)
接下来\(m\)行,每行包含两个正整数\(u_i\),\(v_i\)表示一条单向道路,起点为\(u_i\),终点为\(v_i\)。
输出
输出\(n\)行,每行一个整数,其中第\(i\)行输出到达第\(i\)个街区的最少时间,如果无法到达则输出−1。
样例输入
5 2
5 4 2 3 7
1 4
2 3
样例输出
0
1
2
1
-1
提示
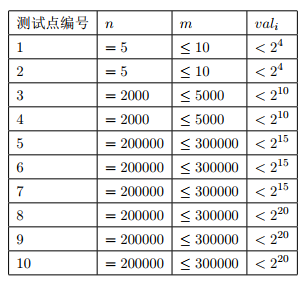
对于 100% 的数据,\(1≤u_i,v_i≤n,1≤val_i<2^{20}\)
40pts:暴力+最短路
最暴力的做法,就是是遍历每点i,再O(n)扫一遍找到所有j使得\(val_i\)&\(val_j\),将i到j连边。
然后跑一遍最短路即可。
代码:
#include<bits/stdc++.h>
const int oo=1061109567;
#define MAXN 2010
using namespace std;
int n,m,head[MAXN],tot,dis[MAXN],val[MAXN],tot2;
struct NN{
int to,last;
}P[MAXN*2];
struct node{
int ed,last;
}G[MAXN*MAXN*2];
void Add(int st,int ed){
++tot;
G[tot]=node{ed,head[st]};
head[st]=tot;
}
struct di{
int d,v;
};
bool operator < (di X,di Y){
return X.d>Y.d;
}
priority_queue<di>Q;
bool vis[MAXN];
int main(){
memset(dis,63,sizeof(dis));
dis[1]=0;
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&val[i]);
}
for(int x,y,i=1;i<=m;i++){
scanf("%d %d",&x,&y);
Add(x,y);
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if((val[i]&val[j])==val[j])Add(i,j);
}
}
Q.push(di{0,1});
while(!Q.empty()){
int now=Q.top().v;
Q.pop();
if(vis[now])continue;
vis[now]=true;
for(int i=head[now];i;i=G[i].last){
int t=G[i].ed;
if(dis[t]>dis[now]+1){
dis[t]=dis[now]+1;
Q.push(di{dis[t],t});
}
}
}
for(int i=1;i<=n;i++){
if(dis[i]!=oo)printf("%d\n",dis[i]);
else puts("-1");
}
return 0;
}
70pts:虚点优化
显然,对于一个二进制数x,若x&y=y,那么显然y是x的子集。
考虑到建虚点,我们可以开\(2^{15}\)个虚点,然后把每个点与其所有子集连边权为0的边。
同时对于每个点i,将i跟\(val_i\)对应的虚点连一条边权为1的边,将\(val_i\)对应的虚点跟i连一条边权为0的边。
不过,由于内存问题,我们不必真正地将这些虚点与其子集连边,可以预处理出每个数对应的子集,访问到该点时直接遍历子集即可。
100pts:虚点再度优化+SPFA(其实BFS就可以了)
把70pts的代码稍微改进一下就可以了。
你会发现,一个虚点,只用与去掉任意一位1的点连边就可以了。比如说:10110,只用与10100,10010,00110连边。
代码:
#include<bits/stdc++.h>
#define MAXN 200010
using namespace std;
const int oo=1061109567;
int n,m,tot,val[MAXN],lian[(1<<20)+10][22],head[MAXN+((1<<20)+10)],dis[MAXN+((1<<20)+10)],he,ta;
struct node {
int ed,v,last;
} G[1000010];
int Q[(1<<21)+10+MAXN];
bool vis[MAXN+((1<<20)+10)];
void Add(int st,int ed,int v) {
++tot;
G[tot]=node {ed,v,head[st]};
head[st]=tot;
}
int main() {
memset(dis,63,sizeof(dis));
scanf("%d %d",&n,&m);
for(int i=1; i<=n; i++)scanf("%d",&val[i]),Add(MAXN+val[i],i,0),Add(i,MAXN+val[i],1);
for(int i=1; i<(1<<20); i++) {
for(int j=1; j<=20; j++) {
if((1<<(j-1))&i)lian[i][++lian[i][0]]=i^((1<<(j-1)));
}
}
for(int i=1,x,y; i<=m; i++) {
scanf("%d %d",&x,&y);
Add(x,y,1);
}
dis[1]=0;
he=1,ta=0;
Q[++ta]=1;
while(he<=ta) {
int now=Q[he++],t,v,x;
vis[now]=false;
if(now<MAXN) {
for(int i=head[now]; i; i=G[i].last) {
t=G[i].ed,v=G[i].v;
if(dis[t]>dis[now]+v) {
dis[t]=dis[now]+v;
if(!vis[t])vis[t]=true,Q[++ta]=t;
}
}
} else {
x=now-MAXN;
for(int i=1; i<=lian[x][0]; i++) {
t=lian[x][i]+MAXN;
if(dis[t]>dis[now]) {
dis[t]=dis[now];
if(!vis[t])vis[t]=true,Q[++ta]=t;
}
}
for(int i=head[now]; i; i=G[i].last) {
t=G[i].ed,v=G[i].v;
if(dis[t]>dis[now]+v) {
dis[t]=dis[now]+v;
if(!vis[t])vis[t]=true,Q[++ta]=t;
}
}
}
}
for(int i=1; i<=n; i++)printf("%d\n",(dis[i]==oo)?-1:dis[i]);
return 0;
}
例题3:POI2010 Railway
题目描述
一个铁路包含两个侧线1和2,右边由A进入,左边由B出去(看下面的图片) 有n个车厢在通道A上,编号为1到n,它们被安排按照要求的顺序(a1,a2,a3,a4....an)进入侧线,进去还要出来,它们要按照编号顺序(1,2,3,4,5。。。。n)从通道B出去。他们从A到1或2,然后经过一系列转移从B出去,不用考虑容量问题。
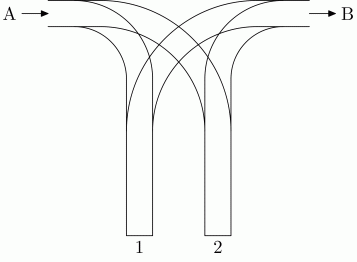
输入
输入:第一行一个整数n(1<=n<=100000)表示要转移的车厢总数,第二行为进入侧线的要求顺序a1.a2.a3.a4....an,由空格隔开。
输出
输出:如果可以按照编号顺序到通道B,则输出两行,第一行为TAK,第二行为n个由空格隔开的整数,表示每个车厢进入的侧线编号(1,2)。否则输出NIE。
样例输入
[样例输入1]
4
1 3 4 2
[样例输入2]
4
2 3 4 1
样例输出
[样例输出1]
TAK
1 1 2 1(1号线进到侧线1,然后出来,3号进入侧线1,4号进入侧线2,2号进入侧线1,然后出来,接着3号出来,4号出来)
[样例输出2]
NIE(不可能。。No)
一种\(O(n^3)\)写法:暴力+二分图染色
不难发现一个性质:
对于车厢\(i,j\),若存在一个\(k\),满足\(i<j<k\)且\(A_k<A_i<A_j\)那么,\(i\)和\(j\)不能在同一个轨道上。
但若直接枚举\(i,j,k\),\(n^3\)的复杂度会让你T飞起来。
所以我们要适当优化。
60分写法\(O(n^2)\):前缀最小值优化
由于只要存在一个k就可以了,故我们可以预处理\(Min\)数组。
其中
那么我们枚举\(i\),\(j\),(\(i<j\))若\(Min_{j+1}<A_i\)则说明此时\(i,j\)是不能入同一个栈的。
然后,我们将不能入同一个栈的\(i\)和\(j\)之间连边,在二分图染色一下是否可行即可。
100分写法\(O(n log(n))\):虚边优化
不难发现,此时有\(n^2\)条边,但只用染\(n\)次,也就是说,很多边是多余的
那我们能不能开一个数据结构,来维护一个点与那些点不能入同一个栈?
这就需要线段树了。
再观察一下这两个式子:
那么,对于一个点x,若其在式子中是当作点i,那么我们就先预处理出\(C_i\)表示满足\(A_{C_i}<A_i\)且\(C_i>i\)的最远的点(\(C_i\)当作点k)。于是我们就可以在下标\([i+1,C_i-1]\)中找一个权值大于\(A_i\)的点(当作点j)
同理,若其当作点j那么,就就找到一个最小的\(A_k\)使得\(j<k\)。于是我们可以在权值\([A_k+1,A_j-1]\)中找一个下标小于j的点(当作点i)
这就可以用线段树了。
当然,为了方便查找,在下标线段树中存最大值,权值线段树中存最小值,查找时随便找一个符合条件的点就行了。
但,这还不行。
在染色时一个点仍会访问到所有与其不能进同一个栈的点,貌似还会是(\(n^2\))。
其实,我们没必要这样,每遍历一个点,就把其在两棵树上都删掉。
可这貌似还有个问题。
若有3节车厢,若1和2,1和3,2和3都不能进同一个,那么在遍历1时,我们把1,2和3都删掉了,此时2的颜色与3的颜色相同,但遍历2时,却遍历不到3了。也就是说,这种情况下会输出"TAK"
其实,这种我们先不用管。在染色完后,每个车厢入的轨道就确定了,我们只需模拟一下这样的进入轨道的方案合不合法。
代码:(本人感觉巨丑,5000多B)
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e5+10;
int n,A[MAXN],Min[MAXN],pos[MAXN],C[MAXN],co[MAXN],ans[MAXN];
queue<int> Q;
struct node {
int L,R,NumVal,PosVal;
} tree[MAXN<<2];
void Up(int p) {
tree[p].NumVal=max(tree[p<<1].NumVal,tree[p<<1|1].NumVal);
tree[p].PosVal=min(tree[p<<1].PosVal,tree[p<<1|1].PosVal);
}
void build(int L,int R,int p) {
tree[p].L=L,tree[p].R=R;
if(L==R) {
tree[p].NumVal=A[L];
tree[p].PosVal=pos[L];
return;
}
int mid=(L+R)>>1;
build(L,mid,p<<1);
build(mid+1,R,p<<1|1);
Up(p);
}
void update(int wz,int p,int x,int kind) {
if(tree[p].L==tree[p].R) {
if(kind==1)tree[p].NumVal=x;
else tree[p].PosVal=x;
return;
}
int mid=(tree[p].L+tree[p].R)>>1;
if(wz<=mid)update(wz,p<<1,x,kind);
else update(wz,p<<1|1,x,kind);
Up(p);
}
int QueryNum(int L,int R,int p,int x) {
if(tree[p].L==tree[p].R) {
if(x<tree[p].NumVal)return tree[p].L;
else return n+1;
}
int mid=(tree[p].L+tree[p].R)>>1;
if(L<=tree[p].L&&tree[p].R<=R) {
if(x<tree[p<<1].NumVal)return QueryNum(L,mid,p<<1,x);
else return QueryNum(mid+1,R,p<<1|1,x);
}
if(R<=mid)return QueryNum(L,R,p<<1,x);
else if(L>=mid+1)return QueryNum(L,R,p<<1|1,x);
else return min(QueryNum(L,mid,p<<1,x),QueryNum(mid+1,R,p<<1|1,x));
}
int QueryPos(int L,int R,int p,int x) {
if(tree[p].L==tree[p].R) {
if(x>tree[p].PosVal)return tree[p].L;
else return n+1;
}
int mid=(tree[p].L+tree[p].R)>>1;
if(L<=tree[p].L&&tree[p].R<=R) {
if(x>tree[p<<1].PosVal)return QueryPos(L,mid,p<<1,x);
else return QueryPos(mid+1,R,p<<1|1,x);
}
if(R<=mid)return QueryPos(L,R,p<<1,x);
else if(L>=mid+1)return QueryPos(L,R,p<<1|1,x);
else return min(QueryPos(L,mid,p<<1,x),QueryPos(mid+1,R,p<<1|1,x));
}
int AskNum(int now) {
if(C[now]-now<2)return n+1;
return QueryNum(now+1,C[now]-1,1,A[now]);
}
int AskPos(int now) {
int l=Min[now+1],r=A[now];
l++,r--;
if(l>r)return n+1;
return QueryPos(l,r,1,now);
}
bool flag=false;
void BFS() {//染色
memset(co,-1,sizeof(co));
for(int i=1; i<=n; i++) {
if(co[i]==-1) {
Q.push(i);
update(i,1,0,1);
update(A[i],1,n+1,0);
co[i]=1;
while(!Q.empty()) {
int now=Q.front();
Q.pop();
int res1[MAXN],res2[MAXN];
res1[0]=0,res2[0]=0;
while("FBZ is my son") {
int t;
bool flag1=true,flag2=true;
t=AskNum(now);
if(t==n+1)flag1=false;
if(flag1) {
update(t,1,0,1);
update(A[t],1,n+1,0);
if(co[t]==-1) {
co[t]=!co[now];
res1[++res1[0]]=t;
Q.push(t);
}
}
t=AskPos(now);
if(t==n+1)flag2=false;
if(flag2) {
t=pos[t];
update(t,1,0,1);
update(A[t],1,n+1,0);
if(co[t]==-1) {
co[t]=!co[now];
res2[++res2[0]]=t;
Q.push(t);
}
}
if(flag1==false&&flag2==false)break;
}
}
}
}
}
int main() {
scanf("%d",&n);
for(int i=1; i<=n; i++)scanf("%d",&A[i]),pos[A[i]]=i;
Min[n+1]=2e9+7;
for(int i=n; i>=1; i--)Min[i]=min(Min[i+1],A[i]);
for(int i=1; i<=n; i++) {
if(Min[i+1]>A[i]) {
C[i]=0;
continue;
}
C[i]=lower_bound(Min+1+i,Min+1+n,A[i])-Min-1;
}
build(1,n,1);
BFS();
if(flag)return 0;
int stk1[MAXN],stk2[MAXN],tot=1;
stk1[0]=stk2[0]=0;
for(int i=1;i<=n;i++){
if(co[i]==0)stk1[++stk1[0]]=A[i];
else stk2[++stk2[0]]=A[i];
while("FBZ is my son"){
bool fl=false;
if(stk1[stk1[0]]==tot&&stk1[0])stk1[0]--,tot++,fl=true;
if(stk2[stk2[0]]==tot&&stk2[0])stk2[0]--,tot++,fl=true;
if(!fl)break;
}
}
for(int i=1;i<=stk1[0]-1;i++){
if(stk1[i]<stk1[i+1]){
puts("NIE");
return 0;
}
}
for(int i=1;i<=stk2[0]-1;i++){
if(stk2[i]<stk2[i+1]){
puts("NIE");
return 0;
}
}
puts("TAK");
for(int i=1; i<=n; i++) {
if(co[i]==1)ans[i]=1;
else ans[i]=2;
}
for(int i=1; i<=n; i++)printf("%d ",ans[i]);
return 0;
}
例题4:Legacy
题目描述
Rick and his co-workers have made a new radioactive formula and a lot of bad guys are after them. So Rick wants to give his legacy to Morty before bad guys catch them.
There are n planets in their universe numbered from 1 to n. Rick is in planet number s (the earth) and he doesn't know where Morty is. As we all know, Rick owns a portal gun. With this gun he can open one-way portal from a planet he is in to any other planet (including that planet). But there are limits on this gun because he's still using its free trial.
By default he can not open any portal by this gun. There are q plans in the website that sells these guns. Every time you purchase a plan you can only use it once but you can purchase it again if you want to use it more.
Plans on the website have three types:
- With a plan of this type you can open a portal from planet v to planet u.
- With a plan of this type you can open a portal from planet v to any planet with index in range [l, r].
- With a plan of this type you can open a portal from any planet with index in range [l, r] to planet v.
Rick doesn't known where Morty is, but Unity is going to inform him and he wants to be prepared for when he finds and start his journey immediately. So for each planet (including earth itself) he wants to know the minimum amount of money he needs to get from earth to that planet.
Input
The first line of input contains three integers n, q and s (1 ≤ n, q ≤ \(10^5\), 1 ≤ s ≤ n) — number of planets, number of plans and index of earth respectively.
The next q lines contain the plans. Each line starts with a number t, type of that plan (1 ≤ t ≤ 3). If t = 1 then it is followed by three integers v, u and w where w is the cost of that plan (1 ≤ v, u ≤ n, 1 ≤ w ≤ \(10^9\)). Otherwise it is followed by four integers v, l, r and w where w is the cost of that plan (1 ≤ v ≤ n, 1 ≤ l ≤ r ≤ n, 1 ≤ w ≤ $10^9 $).
Output
In the first and only line of output print n integers separated by spaces. i-th of them should be minimum money to get from earth to i-th planet, or - 1 if it's impossible to get to that planet.
Examples
Input#1
3 5 1
2 3 2 3 17
2 3 2 2 16
2 2 2 3 3
3 3 1 1 12
1 3 3 17
Output#1
0 28 12
Input#2
4 3 1
3 4 1 3 12
2 2 3 4 10
1 2 4 16
Output#2
0 -1 -1 12
Note
In the first sample testcase, Rick can purchase 4th plan once and then 2nd plan in order to get to get to planet number 2.
题目大意:有n个点,q个计划,每个计划3种:
1.可以从点u到v,花费w
2.可以从点u到区间[l,r]中的任意一点,花费w
3.可以从区间[l,r]中的任意一点到点v,花费w
每个计划可以用任意次。
问:从1号点到其它所有点的最小花费。
方法:线段树维护虚边+SPFA
对于每一个点u到一个区间[l,r],我们可以建个线段树来维护,用类似区间更新的方法把其接到包含这[l,r]区间的节点上,因此线段树中两两点之间的权值应为0
但是,这依然有个问题:由于每个点既需要与他父亲连边,又需要与其儿子连边,那么线段树上就可以从一个点到任一点。而边的权值又为0,那么每个点的最短路径就变成了0了!
因此,我们要开两倍的点,即对于每一个线段树上的点再开个编号。设点p两个编号为A[p],B[p],那么我们就可以以A[p]为起点发出一条路径,以B[p]为终点接受一条路径。这样的话,A[p]应与其父亲A[x]建一条边,B[p]应与其儿子B[x]建一条边,最后用SPFA跑一下最短路即可。
代码:
#include<bits/stdc++.h>
#define int long long
#define MAXN 100010
using namespace std;
int n,q,s,dis[MAXN*8],cnt;
const long long MX=9187201950435737471;
struct node{
int ed,v;
};
vector<node> G[MAXN*8];
struct segment{
int L,R;
}tree[MAXN*8];
queue<int> Q;
bool vis[MAXN*8];
//注意:A[p]=p+cnt,B[p]=p
void build(int L,int R,int p){
cnt=max(cnt,p);
tree[p].L=L,tree[p].R=R;
if(L==R)return;
int mid=(L+R)>>1;
build(L,mid,p<<1);
build(mid+1,R,p<<1|1);
G[p].push_back(node{p<<1,0});
G[p].push_back(node{p<<1|1,0});
}
void build2(int p){
if(p!=1)G[p+cnt].push_back(node{(p/2)+cnt,0});
if(tree[p].L==tree[p].R)return;
build2(p<<1);
build2(p<<1|1);
}
void update(int L,int R,int p,int ed,int v){
if(tree[p].L==L&&tree[p].R==R){
if(ed!=p)G[ed].push_back(node{p,v});
return;
}
int mid=(tree[p].L+tree[p].R)>>1;
if(R<=mid)update(L,R,p<<1,ed,v);
else if(L>=mid+1)update(L,R,p<<1|1,ed,v);
else update(L,mid,p<<1,ed,v),update(mid+1,R,p<<1|1,ed,v);
}
void update1(int L,int R,int p,int l,int r,int v){
if(tree[p].L==L&&tree[p].R==R){
update(l,r,1,p+cnt,v);
return;
}
int mid=(tree[p].L+tree[p].R)>>1;
if(R<=mid)update1(L,R,p<<1,l,r,v);
else if(L>=mid+1)update1(L,R,p<<1|1,l,r,v);
else update1(L,mid,p<<1,l,r,v),update1(mid+1,R,p<<1|1,l,r,v);
}
int query(int p,int num){
if(tree[p].L==tree[p].R)return p;
int mid=(tree[p].L+tree[p].R)>>1;
if(num<=mid)return query(p<<1,num);
else return query(p<<1|1,num);
}
void SPFA(){
int nooo=query(1,s);
dis[nooo]=0;
Q.push(nooo);
vis[nooo]=true;
while(!Q.empty()){
int now=Q.front();
Q.pop();
vis[now]=false;
for(int i=0;i<G[now].size();i++){
int t=G[now][i].ed,v=G[now][i].v;
if(dis[now]+v<dis[t]){
dis[t]=dis[now]+v;
if(!vis[t]){
vis[t]=true;
Q.push(t);
}
}
}
}
}
signed main(){
memset(dis,127,sizeof(dis));
scanf("%lld %lld %lld",&n,&q,&s);
build(1,n,1);
build2(1);
for(int i=1;i<=q;i++){
int t;
scanf("%lld",&t);
if(t==1){
int v,u,w;
scanf("%lld %lld %lld",&v,&u,&w);
update1(v,v,1,u,u,w);
}
else if(t==2){
int v,l,r,w;
scanf("%lld %lld %lld %lld",&v,&l,&r,&w);
if(l>r)swap(l,r);
update1(v,v,1,l,r,w);
}
else if(t==3){
int v,l,r,w;
scanf("%lld %lld %lld %lld",&v,&l,&r,&w);
if(l>r)swap(l,r);
update1(l,r,1,v,v,w);
}
}
for(int i=1;i<=cnt;i++)G[i].push_back(node{i+cnt,0});
SPFA();
for(int i=1;i<=n;i++){
int now=query(1,i);
if(dis[now]==MX)puts("-1");
else printf("%lld\n",dis[now]);
}
return 0;
}

