【codechef】Servers

状压dp

本题特别yy，要好好感受一下

一看到这道题，我们肯定会想到压槽位的使用情况来dp。但仔细一想，槽位上放的服务器不同还会对状态更新产生影响！因此不能压槽位的使用情况。

然后，我就看了下AC人的代码

再琢磨了一会儿，就想通了

先看个例子:

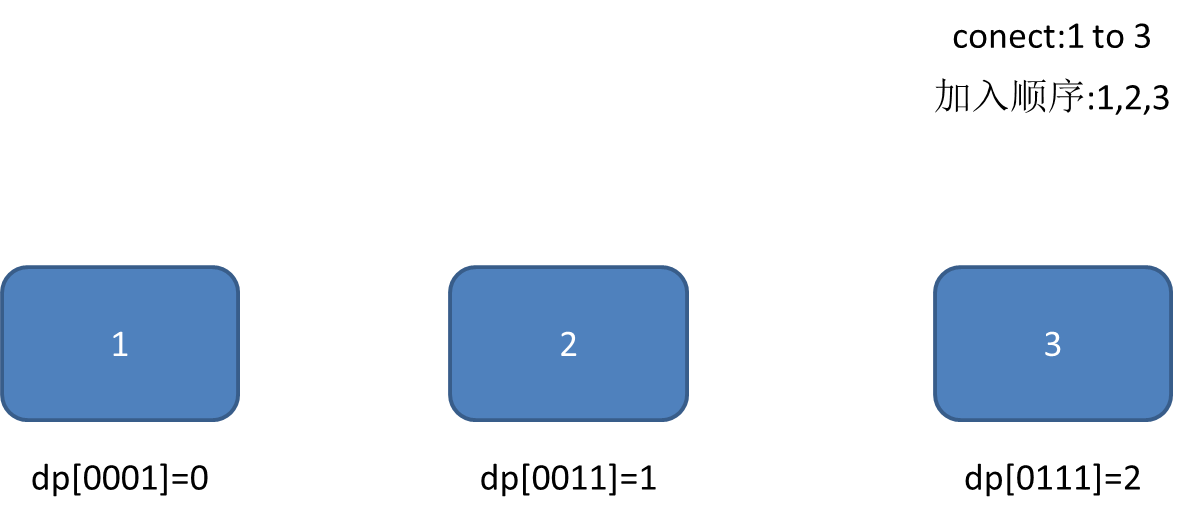
加完后，不难发现，\(dis[1][3]=2\)
而加入顺序为:1,2,3
那么，可以在加入2的时候把值先+1，加入3时再+1

为什么这样是正确的？

因为若第二次加入的是3，那么\(dis[1][3]=1\)，但是加入的却是2。不难想象：加入2后1和3之间至少隔个2，也就是说，\(dis[1][3]\)的最小值为2！

那么就可以加入2时先+1。同理:若第3次加入的是4，那么就再+1，直到加入了3为止。

回到此题:若该状态下有多个点与未在此状态下的点相连，那么操作加的和就是该状态下的与未在此状态匹配的边数。

算法流程：

1.枚举所有服务器的取用状态

2.对于每种状态，找出状态内的点与未在此状态内的匹配边数

3.从未在此状态下的点进行状态转移

那么\(dp[(1<<n)-1]\)

就是最终答案

代码:

#include<bits/stdc++.h>
using namespace std;
//cnt表示每种状态下的"1"的数量 con表示每个服务器的连接情况
int n,m,dp[(1<<20)+10],cnt[(1<<20)+10],con[25];
int main(){
	memset(dp,127,sizeof(dp));
	scanf("%d %d",&n,&m);
	for(int i=1;i<(1<<n);i++)cnt[i]=cnt[i^(i&-i)]+1;
	for(int i=1;i<=m;i++){
		int a,b;
		scanf("%d %d",&a,&b);
		a--,b--;
		con[a]|=1<<b,con[b]|=1<<a;
	}
	dp[0]=0;
	for(int i=0;i<(1<<n);i++){
		int le=((1<<n)-1)^i;
		int add=0;//add表示匹配边数
		for(int j=0;j<n;j++)if((1<<j)&i)add+=cnt[con[j]&le];
		for(int j=0;j<n;j++){
			if((1<<j)&i)continue;
			dp[i|(1<<j)]=min(dp[i|(1<<j)],dp[i]+add);//状态转移
		}
	}
	cout<<dp[(1<<n)-1];
	return 0;
}