悬线法
悬线法
应用：理解并解决最大子矩形问题
SPOJ 1805
题意：
在一条水平线上有 \(n(1\leq n\leq 10^5)\) 个宽为 \(1\)，高为 \(h_1,h_2,\cdots,h_n(0\leq h_i\leq 10^9)\) 的矩形，求包含于这些矩形的最大子矩形面积（图中的阴影部分的面积即所求答案）。
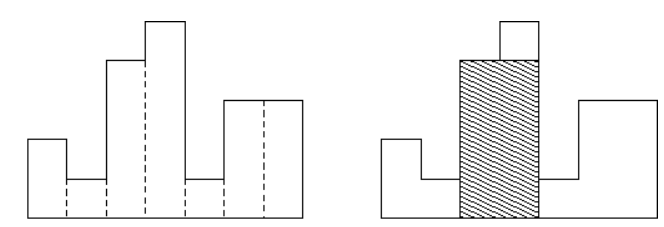
样例输入：
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0
样例输出：
8
4000
知识点：
悬线法
思路：
悬线，就是一条竖线，这条竖线有初始位置和高度两个性质，可以左右移动至其上端点不超过当前位置矩形高度的任意位置。
对于第 \(i\) 条悬线，我们将这条悬线左右移动，求出其最多能向左能移动到的位置 \(l_i\) 和最多能向右移动到的位置 \(r_i\) ，那么包含该悬线的最大子矩形的面积即为 \((r_i-l_i+1)\cdot h[i]\)。容易发现，最大子矩形必定是包含一条初始位置为 \(i\)，高度为 \(h_i\) 的悬线。枚举实现这个过程的时间复杂度为 \(O(n^2)\)，但是我们可以用悬线法将其优化到 \(O(n)\)。
定义 \(l_i\) 为当前 \(i\) 位置的悬线最多能向左能移动到的位置，容易得到 \(l_i\) 初始为 \(i\)，我们需要进一步判断还能不能进一步往左扩展。
- 如果当前 \(l_i=1\)，则已经扩展到了边界，不可以；
- 如果当前 \(h_i>h_{l_i-1}\)，则从当前悬线扩展到的位置不能再往左扩展了；
- 如果当前 \(h_i\leq h_{l_i-1}\)，则从当前悬线还可以往左扩展，并且由此 \(l_i-1\) 位置的悬线能向左扩展到的位置，\(i\) 位置的悬线一定也可以扩展到，于是我们将 \(l_i\) 更新为 \(l_{l_i-1}\)，并继续执行判断。
for (int i = 0; i < n; i++) {
while (l[i] > 0 && h[i] <= h[l[i] - 1]) {
l[i] = l[l[i] - 1];
}
}
此即为悬线法。
求解 \(r_i\) 过程同理。
for (int i = n - 1; i >= 0; i--) {
while (r[i] < n - 1 && h[i] <= h[r[i] + 1]) {
r[i] = r[r[i] + 1];
}
}
时间复杂度：
通过摊还分析教教QvQ，可以证明每个 \(l_i\) 最多会被其他的 \(l_j\) 遍历到一次，因此时间复杂度为 \(O(n)\)。
代码：
typedef long long ll;
const int N = 1e5 + 10;
int l[N], r[N], h[N];
int n;
ll ans;
void solve() {
while (cin >> n && n) {
for (int i = 0; i < n; i++) {
l[i] = r[i] = i;
cin >> h[i];
}
for (int i = 0; i < n; i++) {
while (l[i] > 0 && h[i] <= h[l[i] - 1]) {
l[i] = l[l[i] - 1];
}
}
for (int i = n - 1; i >= 0; i--) {
while (r[i] < n - 1 && h[i] <= h[r[i] + 1]) {
r[i] = r[r[i] + 1];
}
}
for (int i = 0; i < n; i++) {
ans = max(ans, 1ll * (r[i] - l[i] + 1) * h[i]);
}
cout << ans << endl;
}
}
P4147
题意：
给定一个 \(n\times m\) 的包含 'F' 和 'R' 的矩阵，求其面积最大的子矩阵的面积，使得这个子矩阵中的每一位的值都为 'F'。
样例输入：
5 6
R F F F F F
F F F F F F
R R R F F F
F F F F F F
F F F F F F
样例输出：
45
数据规模：
\(1\leq n,m \leq 1000\)
知识点：
悬线法
思路：
我们会发现本题的模型和上一题的模型很像。我们可以每次只考虑某一行的所有元素，记下位置 \((i,j)\) 所在元素最多能向上扩展的距离 \(h_i\)，然后再利用悬线法求解即可。
时间复杂度：
\(O(n^2)\)
代码：
typedef long long ll;
const int N = 1010;
int l[N], r[N], h[N];
int n, m;
char ch;
ll ans;
void solve() {
cin >> n >> m;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
l[j] = j, r[j] = j;
cin >> ch;
if (ch == 'R') h[j] = 0;
else h[j]++;
}
for (int j = 0; j < m; j++) {
while (l[j] > 0 && h[j] <= h[l[j] - 1]) {
l[j] = l[l[j] - 1];
}
}
for (int j = m - 1; j >= 0; j--) {
while (r[j] < m - 1 && h[j] <= h[r[j] + 1]) {
r[j] = r[r[j] + 1];
}
}
for (int j = 0; j < m; j++) {
ans = max(ans, 1ll * (r[j] - l[j] + 1) * h[j] * 3);
}
}
cout << ans;
}
习题
参考：
