阅读笔记-2022.11.23
论文：DEEP BATCH ACTIVE LEARNING BY DIVERSE, UNCERTAIN GRADIENT LOWER BOUNDS
一种基于深度神经网络模型的批量主动学习算法。
NOTATION AND SETTING
\([K] := \{ 1,2,...K \}\)
\(\cal X\) 表示实例空间， \(\cal Y\) 表示标签空间。论文是多分类任务，所以 \({\cal Y} = [K]\) 。
\(D\) 表示抽取样本的分布，\(D_{\cal X}\) 表示未标记的数据分布， \(D_{\cal Y | X}\) 表示给定样本标签上的条件分布。
论文使用基于池的主动学习，学习器接收到一个根据 \(D_{\cal X}\) 采样的无标签数据集 \(U\) ，并可以对任意 \({\cal X} \in U\) 请求根据 \(D_{\cal Y| X}\) 采样的标签。 \(\mathbb{E}_D\) 表示数据分布 \(D\) 下的期望。
给定一个分类器 \(h: {\cal X} \rightarrow {\cal Y}\) ，其将实例映射到标签
一个标记实例 \((x,y)\)
\(h\) 在 \((x,y)\) 上的 \(0/1\) 误差表示为 \({\scr l}_{01} (h(x), y) = I (h(x) \neq y)\)
分类器 \(h\) 的性能由它的预期 \(0/1\) 误差来衡量，即 \(\mathbb{E}_D [{\scr l}_{01} (h(x),y)] = {\rm Pr}_{(x,y) \sim D} (h(x) \neq y).\)
基于池的主动学习的目标是使用尽可能少的标签查询找到预期 \(0/1\) 错误较小的分类器。给定一组 \(S\) 的标记实例 \((x,y)\) ，其中每个 \(x \in S\) 从 \(U\) 中选取，然后进行标记查询，使用 \(\mathbb{E}_S\) 作为 \(S\) 的样本平均值。
由结构固定的底层神经网络 \(f\) 参数化的分类器 \(h\) ，网络中的权重用 \(\theta\) 表示。将带参数 \(\theta\) 的分类器缩写为 \(h_\theta\) 因为体系结构在任何给定的上下文中都是固定的，分类器采用 \(h_\theta (x) = \arg\max_{y \in [K]} f(x;\theta)_y\) ，其中 \(f(x;\theta) \in \mathbb{R}^K\) 是分配给候选标签的分数的概率向量，给定实例 \(x\) 和参数 \(\theta\) 。通过最小化交叉熵损失 \(\mathbb{E}_S [{\scr l}_{CE} (f(x;\theta),y)]\) ，其中 \({\scr l}_{CE} (p,y) = \sum^K_{i=1} I(y=i) \ln 1/ p_i = \ln 1/p_y .\)
ALGORITHM
首先从 \(U\) 中均匀地随机抽取了一组初始的 \(M\) 个例子，并要求提供它们的标签。然后迭代进行，在每一步t进行两个主要计算：梯度嵌入计算和采样计算。具体来说，在每一步 \(t\)，对于池子里的每一个 \(x\)，计算当前模型所偏好的标签 \(\hat{y}\) ，以及相对于网络最后一层的参数，在 \((x, \hat{y}(x))\) 上的损失梯度 \(g_x\) 。给定这些梯度嵌入向量 \(\{g_x : x \in U \}\)，BADGE通过 \(k\)-MEANS++ 初始化方案进行抽样，选择一组点。该算法查询这些例子的标签，重新训练模型，并重复进行。
The gradient embedding
由于深度神经网络是使用基于梯度的方法进行优化的，作者通过梯度的视角来捕捉关于一个实例的不确定性。特别是，如果知道标签会引起相对于模型参数的损失的大梯度，从而对模型进行大的更新，就可以认为模型对一个实例不确定。这种推理的一个难点是需要知道标签来计算梯度。作为一个agent，计算梯度时，就像模型对例子的当前预测是真实的标签一样。假设大多数自然神经网络满足一个共同的结构，相对于最后一层使用这个标签的梯度规范提供了一个由任何其他标签引起的梯度规范的下限。此外，在该假设下，这个假设的梯度向量的长度捕捉了模型对实例的不确定性：如果模型对实例的标签高度确定，那么实例的梯度嵌入将有一个小的规范，反之，对于模型不确定的样本将有一个较大的规范。因此，梯度嵌入既传达了关于模型的不确定性的信息，也传达了在收到一个例子的标签时的潜在更新方向。
The sampling step
文中希望新的标记样本能给模型带来巨大且多样的改变，而不是病态地选取某一类的样本。
在不引入额外超参数的情况下，进行这种选择的一个自然方法是从 \(k\)-Determinational Point Process(\(k\)-DPP) 中取样。也就是说，以与它们的Gram矩阵的行列式成正比的概率选择一批 \(k\) 个点。在这个过程中，当批量大小很低时，选择会自然地倾向于具有大长度的点，这相当于我们空间中的不确定性。当批量较大时，采样器更注重多样性，因为要使 Gram 行列式不为0，需要线性独立，这在大 \(k\) 中更难实现。
不幸的是，从 \(k\)-DPP 中取样并非易事。为了克服计算上的障碍，作者建议使用 \(k\)-MEANS++ 算法来代替采样。 \(k\)-MEANS++ 种子选择中心点的方法是，按照与已经选择的最近的中心点的平方距离的比例迭代采样，这与 \(k\)-DPP 一样，倾向于选择一批不同的高量级的样本。
Example: multiclass classification with softmax activations
一个神经网络 \(f\) ，其中最后一个非线性是 \(\rm softmax\) 即 \(\sigma (z)_i = e^{z_i}/ \sum^K_{j=1} e^{z_j}\) 。具体来说， \(f\) 被 \(\theta= (W,V)\) 参数化，其中 \(\theta_{out} = W = (W_1,...,W_K)^{\top} \in \mathbb{R}^{K \times d}\) 是最后一层的权重， \(V\) 是之前所有层的权重组成的。这意味着 \(f(x; \theta) = \sigma(W \cdot z(x; V ))\) ，其中 \(z\) 是将输入 \(x\) 映射到网络倒数第二层输出的非线性函数。让我们固定一个无标签的样本x，并定义 \(p_i = f(x; \theta)_i\)。则有：
定义 \(g^y_x = \frac{\partial}{\partial W} {\scr l}_{\rm CE} (f(x;\theta),y)\) 为一个标签 \(y\) ，\(g_x = g^{\hat y}_x\) 作为梯度嵌入，其中 \(\hat{y} = \arg \max_{i \in [K]} p_i\) 。那么 \(g_x\) 的第 \(i\) 块（即，对应于标签 \(i\) 的梯度）是：
根据这个表达式，我们可以做如下观察:
- \(g_x\) 的每个块都是 \(z(x; V )\) 的缩放，它是网络倒数第二层的输出。在这方面， \(g_x\) 捕获了 \(x\) 的表征信息，类似于Sener和Savarese的做法
- 下面的Proposition 1 表明，\(g_x\)的规范是真实标签为y的例子相对于最后一层权重所引起的损失梯度的规范的下限，即\(||g_x|| \leq ||g^y_x||\)。这表明， \(g_x\) 的规范保守地估计了例子对当前模型的影响。
- 如果当前模型 \(\theta\) 对 \(x\) 有高度的信心，即向量 \(p\) 偏向于标准基础向量 \(e_j\) ，那么 \(\hat{y}=j\) ，向量 \((p_i-I(\hat{y}=i))^K_{i=K}\) 有一个小长度。因此， \(g_x\) 也有一个小的长度。这种高置信度的例子往往具有小幅度的梯度嵌入，不太可能在迭代 \(t\) 时被 \(k\)-MEANS++ 重复选择。
Proposition 1:
\(\forall y \in \{ 1,...,K \}\) ，使得 \(g^y_x = \frac{\partial}{\partial W} {\scr l}_{\rm CE} (f({x;\theta}), y)\) 则有：
因此有 \(\hat{y} = \arg \min _{y \in [k]} ||g^y_x||\)
根据公式 (1) 有：
第二项来自于 \(\hat{y} = \arg \max_{y \in [K]} p_y\) 。
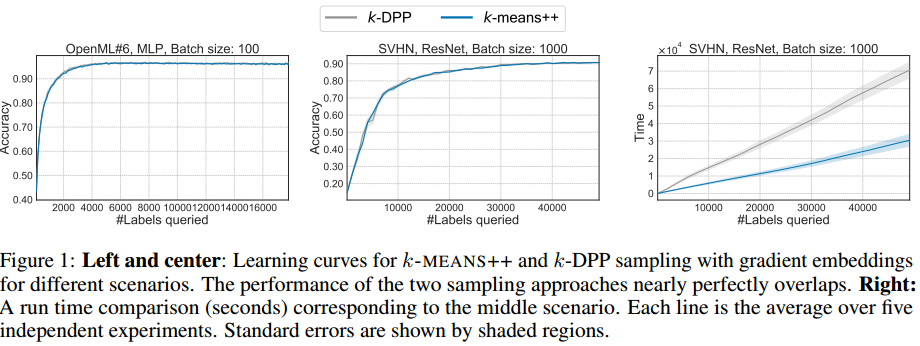
这种简单的取样器倾向于产生类似于\(k\)-DPP 的多样化批次。如图1所示，在两个取样器之间切换并不影响主动学习器的统计性能，但大大改善了其计算性能。
....
