阅读笔记-2022.11.17
论文:Active Learning for Open-set Annotation
现有的主动学习研究通常在封闭设置下工作,假设所有要标记的数据示例都来自已知的类。在实际的注释中,未标记的数据通常包含大量来自未知类的实例,导致大多数主动学习方法的失败。本文为了解决 Open-Set Annotation 问题提出了 LfOSA。
LfOSA框架引入一个辅助网络,用高斯混合模型对每例的最大激活值分布进行建模,可以动态地从未标记集中的已知类中选择概率最高的示例。通过降低损失函数的温度 \(T\),利用已知监督和未知监督,进一步优化检测模型。
The OSA Problem Setting
在 OSA 问题中,一个具有有限标记集 \(D_L\) 和一个巨大的未标记开放数据集 \(D_U\) ,其中 \(D_L = \{ (x^L_i , y_i^L) \} ^{n^L}_{i=1}\) , \(D_U = \{ x_j^U \}^{n^U}_{j=1}\) 。设 \(D_U = X_{kno} \cup X_{unk}\) ,\(X_{kno} \cap X_{unk} \neq \varnothing\) ,\(X_{kno}\) 和 \(X_{unk}\) 分别表示已知类和未知类的例子。每个标记实例 \(x^L_i\) 属于 \(k\) 已知类 \(Y=\{ y_k \}^K_{k=1}\) 中的一个,而未标记实例 \(x^U_j\) 可能属于已知类或未知类。设 \(x^{query}\) 表示每次迭代的查询集,由未知查询集 \(X^{query}_{unk}\) 和 已知查询集 \(X^{query}_{kno}\) 组成,即 \(X^{query} = X^{query}_{unk} \cup X^{query}_{kno}\) 。目标是由选择地构造包含尽可能多的已知实力的查询。
在第 \(i\) 次迭代中,在标记集 \(D_L\) 上训练参数为 \(\theta_C\) 的分类器 \(f_{\theta_C}\) 。根据当前训练的模型,在特定条件下选择一批含有 \(b\) 个实例的 \(X^{query}\) 。查询标签后,对 \(k_i\) 个已知样例 \(X^{query}_{kno}\) 进行标注,标注集更新为 \(D_L = D_L \cup X^{query}_{kno}\) ,将 \(l_i\) 个含有未知类的样例 \(X^{query}_{unk}\) 添加到无效集 \(D_I\) 中,则有 \(b = k_i + l_i\) 。第 \(i\) 次选择中已知类的查全率和查准率可以定义为:
其中 \(n_{kno}\) 代表无标签数据集中已知类的样本数量。 \(recll_i\) 计算在第 \(i\) 次查询后查询的已知实例的数量,\(precision_i\) 表示目标实例在第 \(i\) 次查询中的比例。显然,如果保持较高的 \(precision\) 和 \(recall\) 来准确地选择已知的例子,训练的目标分类器将更有效。
Algorithm Detail
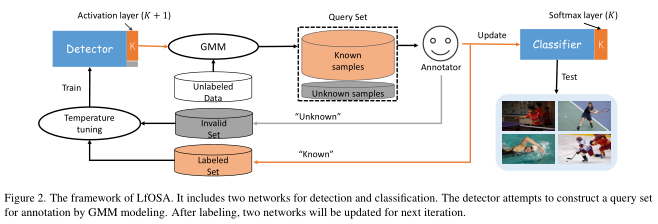
LfOSA的框架 Figure 2 所示,主要由三个部分组成:检测器训练(detector training)、主动采样(active sampling)和分类器训练(classifier training)。
Detector training
除了分类 \(K\) 个已知类,检测器还扩展了一个额外的输出 \((K+1)\)-\(th\) 来预测未知类。对于一个来自有标签或无效数据集给定的实例 \(x\) ,用 one-hot 编码 \(p\) 对它的标签 \(c\) 进行编码,即 \(p_c = 1\) ,其他的值设置为 \(0\) 。利用交叉熵损失训练检测器:
其中 ,\(q_c^T = \frac{\exp(a_c/T)}{\sum_j \exp(a_j/T)}\) , \(a_c\) 为最后一个全连接层的第 \(c\) 个输出值, \(T\) 为温度参数,通常设置为较低值 \((T=0.5)\) ,易产生更尖锐的类别概率分布 \(q^T_c\) 。通过最小化损失函数,已知类的实例在前 \(K\) 维上的激活值较大,在 \((K+1)\)-\(th\) 维上的激活值较小,而未知类的实例则相反。本文发现降低损失函数的温度 \(T\) 可以建议不增强激活层的可区分性。简要分析如下:
当损失函数\({\cal L}_R\)温度下降 \((T \downarrow)\) 时,概率分布 \(q^T_c\) 会更加尖锐,因此有
当 \(\frac{\partial {\cal L}_R}{\partial a_c}\) 变大时,对于激活值 \(a_c\),已知类和未知类的实例将更加容易区分。
Active sampling
OSA任务的目标是从未标记的开放集中精确地选择尽可能多的已知类实例。经过上述对检测器的训练,可以发现网络的激活层(倒是第二层)具有区分未知实例的能力,即未知类实例的最大激活值(MAV)往往与已知类实例的平均MAV有显著差异。形式上,对于每个预测类 \(c\) 的无标记实例 \(x_i\) ,其最大激活值 \(mav^c_i\) 定义如下:
所有未标记的实例将根据当前检测器的预测分为 \(K + 1\) 类。我们可以选择预测为前 \(K\) 个已知类的实例j进入下一个循环,同时过滤掉预测为“未知”的实例。然后,对于每个已知类 \(c\) ,我们使用 Expectation-Maximization 算法将一个双组分GMM(一个用于已知类,另一个用于未知类)拟合到 \(mav^c\) ,其中 \(mav^c\) 是一组带有预测类 \(c\) 的激活值。
其中 \({\cal W}^c\) 为 \(c\) 类的概率。对于 \(c\) 类的每个未标记示例 \(x_i\),其已知概率 \(w_i\in W_c\) 为后验概率 \(p(g|mav_i)\) ,其中g为均值较大(激活值较大)的高斯分量。然后将所有类别的概率归并排序:
接下来,选择概率最高的前 \(b\) 个示例作为请求注释的查询集。换句话说,我们可以通过在 \(w_i\) 上设置一个阈值 \(\tau\) 来获得查询集 \(X^{query}\),其中 \(\tau\) 等于已知的第 \(b\) 大概率:
在查询它们的标签之后,将分别通过添加 \(X^{query}_{kno}\) 和 \(X^{query}_{unk}\) 来更新已标记的未知的集合。

Classifier training
在当前标记数据 \(D_L\) 的基础上,通过最小化标准交叉熵损失来训练 \(K\)-类分类器:
其中, \(( x_i , y_i ) \in D_L\) , \(n^L\) 为当前 \(D_L\) 的大小。
算法1总结了该方法的过程。首先,给出一个小的标记数据集 \(D_L\) ,查询批次大小 \(b\) 和温度 \(T\) 。然后对检测器 \(\theta_D\) 和分类器 \(\theta_C\) 进行随机初始化,将无效集 \(D_I\) 初始化为空集。在每次迭代中,我们通过对所有未标记的例子最小化公式(3)到推理 \(mav^c_i\) 来训练检测器。接下来,对每一类,我们收集由检测器预测和模型每个实例的 \(MAV\) 设定的 \(MAV\) ,以获得已知概率。然后对这些概率进行归并排序,选取概率最高的前 \(b\) 个样本作为请求标注的查询集。因此,分类器 \(\theta_C\) 、标记集和无效集可以被更新并输出到下一次迭代中。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号