阅读笔记-2022.11.15

论文：Active Learning by Feature Mixing

目录

• 问题定义(Problem Definition)
• 特征混合 (Feature Mixing)
• 优化插值参数 \(\pmb \alpha\)(Optimising the Interpolation Parameter \(\pmb \alpha\))
• 候选选择(Candidate Selection)

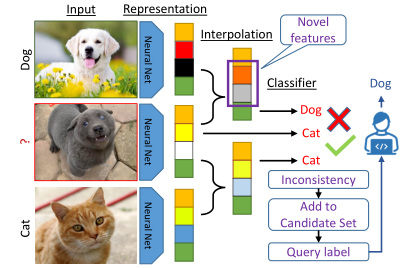
问题定义(Problem Definition)

在不丧失一般性的前提下，学习目标是训练一个具有 K 类的有监督的多分类问题。模型在于Oracle的交互中被积极地训练。在每次迭代中，这个主动学习者都可以访问一小组标记数据 \({\cal D} ^l = \{ ({\pmb x}_i, y_i) \}^M_{i=0}\) ，其中 \({\pmb x} \in {\cal X}\) 代表输入（如，一个图像或者视频片段），\(y_i \in {1,...,K}\) 代表相关的类别标签。模型还可以访问一组未标记的数据 \({\cal D}^u\) ，Oracle从其中选择 \(B\) 个实例进行标记。然后将标记的样本添加到 \(D^l\) 以更新模型。模型的性能在一个不可见的测试数据集上进行评估。

深度神经网络 \(f = f_c \odot f_e\) 通过 \(\theta = \{{\pmb \theta}_e, {\pmb \theta}_c \}\) 参数化。其中，$f_e : {\cal X} \rightarrow \mathbb{R}^D $ 是将输入编码为潜在空间中的D为表示主干，即 \(z = f_e({\pmb x};{\pmb \theta}_e)\) 。除此之外，\(f_c : \mathbb{R}^D \rightarrow \mathbb{R}^K\) 是一个分类器，如多层感知器（MLP），它将实例从它们的表示映射到它们对应的对数 \(p(y|z;{\pmb \theta}) = \text{softmax} (f_c (z;{\pmb \theta}_c))\) 。通过最小化标记集上的交叉熵损失来优化端到端参数：

\[\mathbb{E}_{({\pmb x,y} ) \sim {\cal D}^l} [{\scr l} (f_c \odot f_e ({\pmb x};{\pmb \theta}),y)] \]

对于不可见实例的标签（即伪标签）的预测为 \(y^*_z = \arg \max_y f^y_x (z;{\pmb \theta}_c)\) ，其中 \(z = f_e ({\pmb x};{\pmb \theta_e})\) ， \(f^y_c\) 是 \(y\) 类的 logit 输出。此外，预测标签的 logit 表示为 \(f^*_c (z ) : = f^{y^*_z}_c (z)\) 。还将 \(\pmb Z_u = \{ f_e (\pmb x) ,\forall \pmb x \in {\cal D}^u \}\) 表示为代表未标记数据的集合， \({\pmb Z}^l\) 表示为对应的标记数据。

特征混合 (Feature Mixing)

潜在空间的特征在确定最有价值的样本进行标记方面起着至关重要的作用。作者认为模型的错误预测主要是由于输入中无法识别的新“特征”。因此，通过首先探测模型学习到的特征来解决人工智能问题。为此，论文使用特征的凸组合（即插值）来探索每个为标记点附近的新特征。形式上，作者考虑在未标记和标记实例的表示之间的差值，\({\pmb z}^u\) 和 \({\pmb z}^*\) 分别为 \(\tilde{{\pmb z}}_{\pmb \alpha} = {\pmb \alpha} {\pmb z}^* + (1 -{\pmb \alpha}) {\pmb z}^u\) ，利用插补比 \({\pmb \alpha } \in [ 0, 1\big)^D\) 这一过程被视为一种对新实例进行抽样的方法，而无需显式地对标记实例和未标记实例的联合概率建模：

\[{\pmb z} \sim p({\pmb z}|{\pmb z}^u, {\pmb Z}^* , {\pmb \alpha}) \equiv {\pmb \alpha} {\pmb z}^* + (1 - {\pmb \alpha}) {\pmb z^u, \ \ {\pmb z}^* \sim {\pmb Z}^*} \tag{1} \]

作者用所有代表不同类别的anchor来插插值一个无标签的实例，通过考虑模型的预测如何变化来发现足够明显的特征。为此，作者研究了无标记实例的伪标签(即\(y^*\))的变化以及插值过程中产生的损失。作者期望对标记数据进行足够小的插值不会对每个未标记点的预测标记产生相应的影响。

使用一阶泰勒关于 \({\pmb z}^u\) 展开式，模型在预测无标签实例域有标签实例插值时的伪标签损失可以改写为：

\[\begin{align} \tag{2} {\scr l} (f_c ( \tilde{\pmb z}_{\pmb \alpha} ) ,y^* ) \approx {\scr l} ( f_c ({\pmb z }^u) , y^* )+ ({\pmb \alpha} ({\pmb z }^* - {\pmb z }^u) )^{\tt T} \cdot \nabla_{{\pmb z }^u} {\scr l} (f_c({\pmb z }^u),y^*), \end{align} \]

对于一个足够小的 \(\pmb \alpha\) ，如 \(|| \pmb \alpha || \leq \epsilon\) 几乎是精确的。因此，对于完整的标记集，通过选择两边的最大损失，有：

\[\begin{align} \tag{3} \max_{{\pmb z}^* \sim {\pmb Z}^*} [{\scr l} (f_c(\tilde{\pmb z}_{\pmb \alpha}), y^* ) ] - {\scr l} (f_c({\pmb z}^u), y^*) \approx \max_{{\pmb z}^* \sim {\pmb Z}^*} [({\pmb \alpha}({\pmb z}^* - {\pmb z}))^{\tt T} \cdot \nabla_{{\pmb z }^u} {\scr l} (f_c({\pmb z }^u),y^*) \end{align} \]

直观地说，再进行插值时，损失的变化与两个条件成正比：

• \({\pmb z}^*\) 和 \({\pmb z} ^u\) 的特征的差异与它们的插值 \(\pmb \alpha\) 成正比，
• 损失的梯度与未标记的实例的关系。

前者决定了哪些特征是新的，以及它们的价值如何在有标签和无标签的实例之间有所不同。后者决定了模型对这些特征的敏感性。也就是说，如果有标签的实例和无标签的实例的特征完全不同，但模型时合理一致的，那么损失最重没有变化，因此这些特征不被认为是模型的新特征。

\(\pmb \alpha\) 的选择是针对输入的，决定了要选择的特征。

优化插值参数 \(\pmb \alpha\)(Optimising the Interpolation Parameter \(\pmb \alpha\))

由于手动选择 \(\pmb \alpha\) 的值是不容易的，所以作者设计了一个简单的优化方式，为一个给定的未标记的实例选择适当的值。从公式（3）中可以看出，当选择 \(\pmb \alpha\) 是插值点的损失最大化时，是损失变化最大的最坏的情况。利用公式 （3），作者将选择 \(\pmb \alpha\) 的目标设计为：

\[\tag{4} {\pmb \alpha}^* = {\arg \max}_{||{\pmb \alpha} \leq \epsilon||} ({\pmb \alpha} ({\pmb z}^* - {\pmb z} ^u))^{\tt T} \cdot \nabla_{{\pmb z}^u} {\scr l} ( f_c ({\pmb z}^u) , y^* ) , \]

其中， \(\epsilon\) 是一个管理混合程度的超参数。直观地说，这种优化为每个未标记的实例和anchor选择了最难的 \(\alpha\) 情况。论文使用对偶规范公式对这一优化的解决方案进行近似，在使用2-norm的情况下，可以得到：

\[\tag{5} {\pmb \alpha}^* \approx \epsilon \frac{||( {\pmb z}^* - {\pmb z}^u )||_2 \nabla_{{\pmb z}^u} {\scr l} (f_c({\pmb z}^u), y^*)} {|| \nabla_{{\pmb z}^u} {\scr l} (f_c ({\pmb z}^u), y^*) ||_2} \varnothing ({\pmb z}^* - {\pmb z}^u), \]

其中，\(\varnothing\) 代表元素间的除法。这种近似方法使插值参数的优化变得有效，论文的实验表明，与直接优化 \(\pmb \alpha\) 以使损失最大化相比，它不会对最终结果产生明显的不利影响。

候选选择(Candidate Selection)

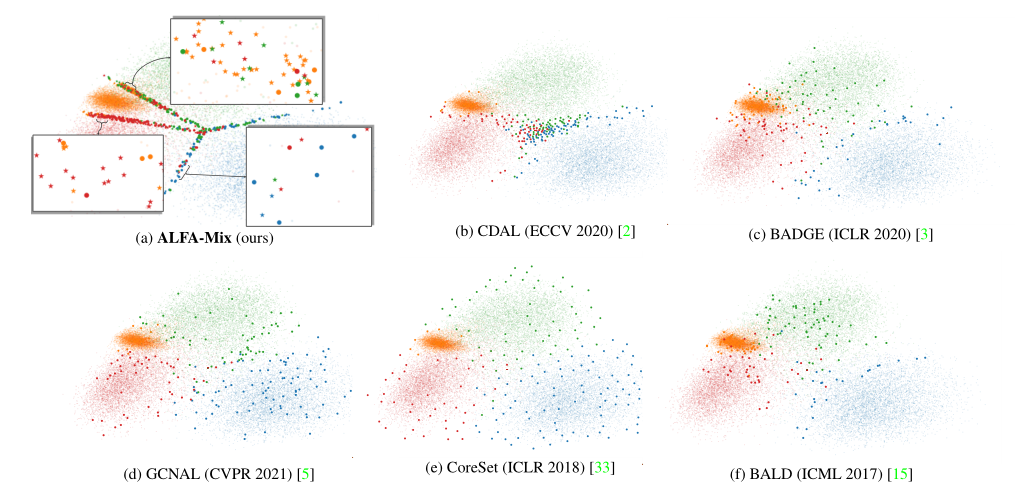
对于AL来说，根据公式（3），选择那些损失随着插值而大幅改变的实例进行查询是合理的。这对应于那些模型的预测发生变化并具有新特征的实例。直观地说，如图2(a)所示，这些样本被放置在潜在空间的决策边界附近。另外，当模型对输入特征的识别有合理的信心时，小的插值不应该影响模型的损失。候选集为：

\[{\cal I} = \{ {\pmb z}^u \in {\pmb Z}^u | \exists{\pmb z}^* \in {\pmb Z}^*, f_c^* (\tilde{\pmb z}_{\pmb \alpha}) \neq y^u_{{\pmb z}^u} \}. \tag{6} \]

所选集合 \(\cal I\) 的规模有可能大于预算 \(B\) 。此外，在理想情况下，我们寻求多样化的样本，因为 \(\cal I\) 中的大多数实例可能是从同一区域选择的（即它们可能具有相同的新特征）。因此，作者建议将 \(\cal I\) 中的实例根据其特征的相似性分为 \(B\) 组，并进一步选择离每个组中心最近的样本，由甲骨文进行标记。这就保证了 \(\cal I\) 样本所代表的空间密度可以通过 \(B\) 实例得到合理的近似。简单地使用k-MEANS，它被广泛使用。