学习日志-2021.10.02

学习日志-2021.10.02

文献阅读：

博弈论与多智能体强化学习

• 重点讨论强化学习技术在多智能体系统中的应用。
• 描述了一个基于对博弈论的经济研究的基本学习框架，并说明了在这种系统中出现的额外复杂性，以及分析学习结果的工具。

Introduction

• 多智能体博弈标准模型

• 系统是分散的。因为需要满足多个可能冲突的目标，或者仅仅是一个集中的控制器需要许多资源，所以数据或控制在物理上是分布式的。
• 智能体自主的实体，有个人的目标和独立的决策能力，但也受到彼此的决策约束的影响。
• 无状态博弈技术和马尔可夫博弈技术
  • 前者专注于处理多智能体交互，而假设环境是平稳的
  • 后者同时处理多智能体交互和动态环境。
  • 

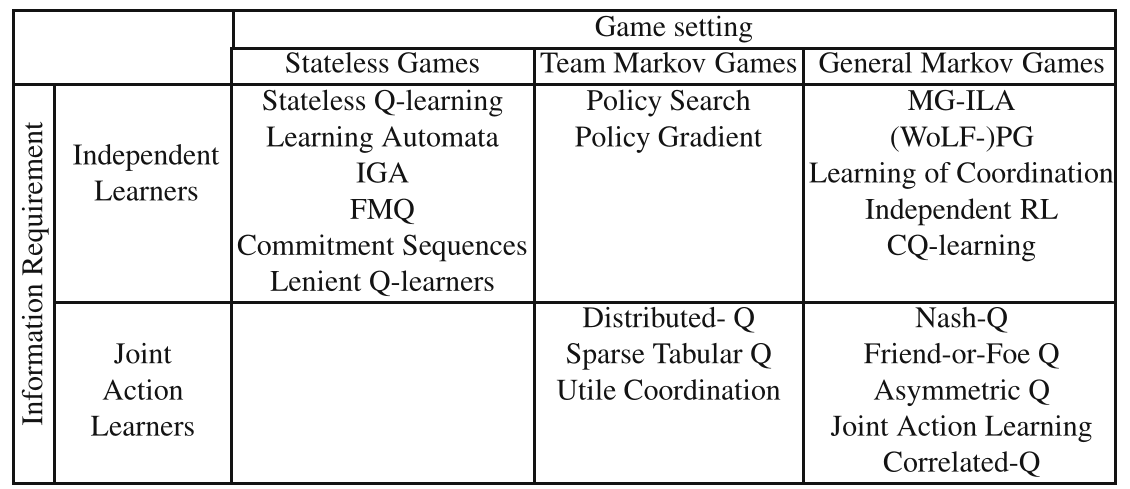
Repeated Games

• 博弈理论

  • 博弈是一个数学对象，它根据个体收益描述了玩家策略之间的互动结果。

• 标准博弈

  • 定义

    • 标准博弈是一个元组 \((n,A_{1,...,n},R_{1,...,n})\) ，其中：
      • \(1,...,n\) ：游戏参与者的集合（玩家）
      • \(A_k\) ：参与者 \(k\) 的动作集合
      • \(R_k\) ：表示参与者 \(k\) 在动作 \(a∈A_1×...×A_n\) 中获得的预期收益。

    游戏是通过允许每个玩家从其私有动作集 \(A_k\) 中独立选择一个单独的动作来进行的。

  • 策略 \(\sigma_k\)

    • \(\mu (A_k)\) ：是参与人 \(k\) 的动作集 \(A_k\) 的概率分布的集合。 \(A_k → [0,1]\) 是 \(\mu (A_k)\) 的一个元素。

    • 纯策略：如果 \(\sigma_k (A) = 1 ∈A_k\) ，其他所有的 \(\sigma_k (A)\) 为0。（否则为混合策略）

    • 在标准博弈中有一个重要的假设，即玩家策略的预期收益是线性的，也就是说，对于策略配置σ，玩家的预期回报是:

      \[R_k (\sigma) = \sum_{a∈A} \prod_{j=1}^n \sigma_j (a_j) R_k (a) \]

• 博弈类型

  • 。。。

• 博弈中的解决方案概念

  由于游戏中的玩家拥有依赖于其他玩家行动的个人奖励功能，所以游戏的预期结果往往无法明确定义。我们不能简单地期望参与者最大化他们的收益，因为所有参与者不可能同时达到这个目标。

  • 当玩家采取最佳响应时，他的收益相对于对手的当前策略是最大化的，也就是说，如果游戏中的其他参与者保持策略不变，那么玩家不可能提高自己的奖励。

    设 \(\sigma = (\sigma_1,...,\sigma_n)\) 是一个策略集； \(\sigma_{-k}\) 表示不包括参与者k的策略 \(\sigma_k\) 的策略集，若有：

    \[R_k (\sigma_{-k}∪\sigma_k^* )≥ R_k (\sigma_{-k} ∪ \sigma'_k) ∀ \sigma'_k ∈ \mu (A_k) \]

    则策略 \(\sigma_k^*∈ \mu (A_k)\) 称为参与者k的最佳响应。

  • 纳什证明了每个标准博弈至少有一个纳什均衡（可能在混合策略中）。在纳什均衡中，所有参与者都采取最佳响应，这意味着每个参与者都对其他参与者的当前策略采取最佳对策，则博弈中的任何参与者都不能通过单方面的偏离均衡来提高收益，想逃离纳什均衡则必须有多个参与者同时改变自己的策略。

• 博弈论中的强化学习

  • 强化学习的目标

    • 由于通常情况下，博弈中的所有参与者都不可能同时最大化自己的收益，大多数强化学习的方法都试图实现纳什均衡。但纳什均衡存在一定的局限性：

      • 纳什均衡不一定唯一，这导致均衡选择的问题。纳什均衡的方法不能保证参与者有唯一的结果，也不能保证参与者有唯一的回报。
      • 在一个纳什均衡中，参与者可能有不同的预期收益，不同的参与者可能会倾向于不同的均衡结果，这意味着需要注意确保参与者才一个纳什均衡中协调。
      • 纳什均衡并不能保证最优，纳什均衡保证了没有一个参与者可以通过单方面改变策略来提高收益，但它不能保证参与者全局收益最大化，甚至不能保证参与者同时做得更好。（一个博弈有可能产生非纳什均衡结果，尽管如此，它还是有可能会给所有参与者带来比纳什均衡下更高的收益，如囚徒困境）

    • 虽然纳什均衡经常被用作学习的主要目标，但它并不是博弈论中唯一可能的解概念。如相关均衡（CE）、进化稳定策略（ESS）等。每种均衡都有自己的应用和优缺点，需要根据问题需要进行选择。

    • 遗憾的概念：

      遗憾是一个智能体实现的收益与该智能体使用某种固定策略所能获得的最大收益之间的差值。

      \[R_T = \max_{a∈A_k} \sum_{t=1}^T R_k (a_{-k}(t)∪\{ a \}) - R_k(a(t)) \]

      大多数基于遗憾的学习方法都试图最小化学习者的平均遗憾 \(R_T/ T\) 。为了确定 \(R_k (a{-k}(t)∪{a})\) 项，精确计算这种遗憾需要了解报酬函数并观察其他智能体的行为。如果没有这方面的数据，遗憾只能根据以前的意见来估计。