学习日志-2021.09.27

学习日志-2021.09.27

论文阅读：

复杂网络上的合作行为演化研究 ——基于 Q-learning 算法

引言

研究背景

• 演化博弈论：理解合作行为如何在自私个体当中涌现和维持。

  • 博弈个体是有限理性的。不能通过一次选择就可以实现策略均衡，而是需要不断地进行策略学习及调整。
    • 在符合条件的困境模型背景下，将参与者作为研究对象，并为其赋予固定的策略集。
    • 指定初始化条件以后，每轮博弈中所有参与者将与敌手进行策略交互来获取相应的收益，再根据学习规则完成策略的更新。
    • 重复上述过程，最终系统中所有博弈个体将会达到某种动态的演化稳定均衡点（非确定的纳什均衡）。

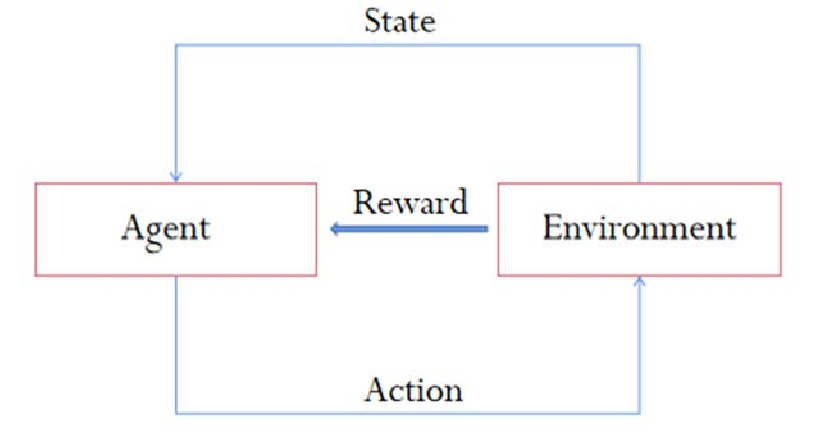
• 强化学习的基本思想是指智能体在与环境进行交互过程中，通过不断“试错”，逐步优化自己的学习策略，以使目标奖励最大化。

研究意义

• 理论意义
  • 加强强化学习算法与演化博弈理论的研究深度，并且，还能够为合作行为的演化带来新的认识。除此之外，亦能够为控制论、生态生物学、心理学以及认知学等其他学科的发展带来相应的启发与思考。
• 现实意义
  • 为解决生态、经济和人类社会中合作行为的存在以及维持提供了清晰的理论框架，有助于我们从新的角度去认识和理解生态、经济以及人类社会中的一些合作行为

国内外研究综述

• 复杂网络的发展
  • 1992年，Martin A. Nowak 提出在囚徒困境问题的探究中将网络的空间结构引入在内。每个参与者会把自己当轮的收益与零剧中的最高收益作为对比，进而决定是否学习该邻居的策略，可以视为合作或背叛策略从一个结点到另外一个结点的传播。研究发现，空间结构的引入给合作者的幸存提供了条件，合作者可以通过在网络上形成互助的团簇来提高自身的适应度，从而低于背叛者的入侵。
  • 1998年，Duncan J. Watts及其导师Steven H. Strogat将高集聚系数和低平均路径长度作为特征，提出瓦茨-斯特罗加茨模型（最经典的小世界网络模型，WS模型）
  • 1999年，Albert-Laszlo Barabasi以及Eric Bonabeau发现许多复杂网络的度分布都近似服从幂律分布，在这一基础上引入了无标度网络的概念。
• 除了Well-mixed和网络结构人群中均衡理论的研究外，学者们同样关注于在任何情况下可以消除社会困境带来的不理解过。共演化机制（个人策略和网络拓扑结构的共同进化）亦成为合作问题研究的一个新的突破方向。
• 强化学习方法
  • Q-learning算法，是Markov决策过程的一种变化形式，通过利用智能体所经历的动作序列来选择下一步的最优动作。这一算法具有环境无关性，不需要建立环境模型。

    • Minimax Q-learning算法，可应用于两人零和博弈；

      • 初始化 \(Q_i (s_i,a_i,a_{-i}) , V_i (s),\pi _i\)

      • For iteration do:

        • 第\(i\)个智能体根据当前状态\(s\)采用探索-利用策略的到动作\(a_i\)并执行

        • 得到下一个状态 \(s'\) ，以及智能体 \(i\) 获得的奖励 \(r_i\) ，并且观测智能体 \(-i\) 在状态s执行的策略\(a_{-i}\)

        • 更新 \(Q_i(s,a_i,a_{-i})\) ：

          $$Q_i(s,a_i,a_{-i}) ← (1 - \alpha) Q_i(s,a_i,a_{-i})+\alpha [r_i+ \gamma V_i (s')]$$

        • 利用线性规划求解 \(V_i^* (s) = \max_{\pi (s')} \min \sum_{a_{-i} ∈A_{-i}} Q_i^* (s,a_i,a_{-i}) \pi (s_i,a_i),i=1,2\)并更新 \(V_i(s)\) 与 \(\pi_i (s')\)

      • End for

      在利用线性规划求解中需要不断求解一个线性规划，这将造成学习速度的降低，增加计算时间。

      为了求解 \(V_i^*(s)\) ，智能体 \(i\) 需要知道所有智能体的动作空间，这个在分布式系统中将无法满足。

      只满足收敛性，不满足合理性。Minimax-Q算法能够找到多智能体强化学习的纳什均衡策略，但是假设对手使用的不是纳什均衡策略，而是一个较差的策略，则当前智能体并不能根据对手的策略学习到一个更优的策略。该算法无法让智能体根据对手的策略来调节优化自己的策略，而只能找到随机博弈的纳什均衡策略。

    • Nash Q-learning算法，适用于多人一般和博弈；

      • 初始化 \(Q_i(s,a_1,...,a_n)=0,∀a_i∈A_i\)

      • For iteration do:

        • 第\(i\)个智能体根据当前状态\(s\)采用探索-利用策略的到动作\(a_i\)并执行

        • 得到下一个状态 \(s'\) ，以及智能体 \(i\) 观测所有智能体的奖励 \(r_1,...,r_n\) ，并且观测所有智能体在状态s执行的策略\(a_1,...,a_n\)

        • 更新 \(Q_i(s,a_1,...,a_n)\) :

          \[Q_i(s,a_1,...,a_n) ← (1 - \alpha) Q_i(s,a_1,...,a_n)+\alpha [r_i+ \gamma NashQ_i (s')] \]

        • 利用二次规划求解状态 \(s\) 处的纳什均衡策略并更新 \(NashQ_i(s)\) 与 \(\pi_i (s')\)

      • End for.

      该算法需要观测其他所有智能体的动作 \(a_i\) 与奖励值 \(r_i\) 。并且与Minimax-Q算法一样，只满足收敛性，不满足合理性。只能收敛到纳什均衡策略，不能根据其他智能体的策略来优化调剂自身的策略。

    • Friend-or-Foe Q-learning算法，可巧妙地求解多智能体一般和博弈中的纳什均衡解。

      • 初始化 \(V_i (s) = 0,Q_i (s,a_1,...,a_n,o_1,...o_{n_2})=0\)， \((a_1,...,a_n)\) 表示 \(i\) 所有 \(friend\) 的动作， \((o_1,...,o_{n_2})\) 表示 \(i\) 所有 \(foe\) 的动作

      • For iteration do：

        • 第\(i\)个智能体根据当前状态\(s\)采用探索-利用策略的到动作\(a_i\)并执行

        • 得到下一个状态 \(s'\) ，以及智能体 \(i\) 观测自身的奖励 \(r_i\) ，并且观测所有 \(friend\) 的动作 \((a_1,...,a_{n_1})\) 与所有 \(foe\) 的动作 \((o_1,...,o_{n_2})\)

        • 更新 \(Q_i (s,a_1,...,a_n,o_1,...,o_{n_2}) = 0\) ：

        \[Q_i (s,a_1,...,a_n,o_1,...,o_{n_2}) ← (1 - \alpha) Q_i (s,a_1,...,a_n,o_1,...,o_{n_2}) + \alpha [r_i + \gamma V_i (s') ] \]
        • 利用线性规划求解状态 \(s'\) 处的纳什均衡策略并更新 \(V_i (s)\) 与 \(\pi_i (s')\) ，更新公式如下：
        \[V_i (s) = \max _{\pi_1 (s'),...\pi_{n_1} (s')} \min_{o_1,...,o_{n_2}∈O_1×...×O_{n_2}} \sum _{a_1,...,a_{n_1}∈A_1×...×A_{n_1}} Q_i (s,a_1,...,a_{n_1},o_1,...o_{n_2}) \pi_1 (s,a_1),..., \pi_{n_1} (s,a_{n_1}) \]

      • End for.

      有一种利用Minimax-Q算法进行多人博弈方法为，两队零和博弈，将所有智能体分成两个小组进行零和博弈。两队零和博弈中每一组有一个leader才控制这一队智能体的所有策略，获取的奖励值也是这一个小组的整体奖励值。

      FFQ算法没有team learder，每个人选择自己动作学习自己的策略获得自己的奖励值，但是为了更新 \(Q\) 值，每个智能体需要在每一步观测其他所有friend与foe的执行动作。

      FFQ与Minimax-Q算法一样都需要利用线性规划，因此算法整体学习速度会变慢。

预备知识

困境模型

经典博弈论包含三个基本要素：参与者、策略集、收益。

在经典博弈论的研究中，参与者将遵循“理性人”假设，他们将以个人利益最大化为目标，根据计算与判断理智地做出决策。这样一来，往往会导致个人最佳选择与集体最佳选择恰好相反。

• 囚徒困境模型

• 公共物品博弈模型

  （以上模型已经了解过，故不再详细记录）

演化博弈论

经典博弈论：个体是完全理性的（所有个体都知道其他人是理性的，每个人都选择采取纳什均衡状态下个人的最优策略）

演化博弈论：博弈参与者是有限理性的

• 重要概念：进化稳定策略——指的是当一个种群中的绝大多数个图都选择了该策略时，即使有一小部分群体突发选择了其他策略，它们依然无法入侵到该种群之中去。

• 复制动力学方程的核心思想：适应度越大的个体，其繁殖能力越强。

  • 形式： \(\acute{x} = x (f_c (x)-\bar{f} (x))\)

    • \(x\) 表示的是选择合作策略的个体所占的人口比例

    • \(f_c (x)\) 表示的是这部分个体对应的适应度。

    • \(\bar{f} (x)\) 表示该种群所有个体的平均适应度

      \[\bar{f} (x) = x f_c (x) + (1-x) f_d (x) \]

    • 当 \(f_c(x) > \bar{f} (x)\) 时，选择合作策略的个体所占比重将增大；

      当 \(f_c(x) < \bar{f} (x)\) 时，选择合作策略的个体所占比重将减小。

基于复杂网络的博弈演化

• 研究基本思路

  • 确定博弈模型（囚徒困境、公共物品博弈等）

  • 确定网络结构（规则格子网络、随机网络、小世界网络等）

  • 确定参与个体的策略更新方式。产检规则一般有如下：

    • 学习最优者：将自己与邻居前一回合的收益对比。直接学习收益最高的个体（包括自身）对应的策略。

    • 模仿优胜者：每轮博弈中，当中心个体 \(x\) 被选中更新策略时，它将找到比自己收益高的邻居 \(y\) ，以正比于 \(y\) 适应度的概率学习其策略。如果 \(x\) 的收益就是最高的，就保持不变。

    • 概率更新。最常见的时费米更新规则，即根据更加符合有限理性假设的学习方式更新器策略，学习概率如下：

      \[W_{S_x←S_y} = \frac {1} {1 + \exp[ (P_x-P_y) / K ]} \]

      其中， \(x\) 和 \(y\) 分别表示中心个体及其邻居， \(S_x\) 和 \(S_y\) 分别对应 \(x\) 及 \(y\) 的策略。 \(P_x\) 和 \(P_y\) 分别为 \(x\) 及 \(y\) 的利益。 \(K\) 代表噪声因素，当 $ K→0 $ 时，表示个体完全理性，只要 $ P_x > P_y $ ，就会直接学习 \(y\) 的策略；而当 $ K → ∞$ 时，个体会随机（以0.5的概率）学习 \(y\) 策略。

  • 进行复杂网络上的演化博弈

强化学习算法

• 机器学习按照学习方式进行分类，可以分为：监督学习、非监督学习和强化学习三种。

  与监督学习和非监督学习相比，强化学习无需依赖大规模的已有数据集（智能体在与环境进行交互的过程中，通过不断接收到的反馈信息来逐步调整自己的动作，以达到最优的状态）。

  

• 马尔可夫决策（MDP）

  • MDP可用元组来表示 \(<S,A,R,P>\) （ \(<S,A,R,P, \gamma >\) ）

    • \(S\) ：状态空间
    • \(A\) ：动作空间
    • \(R_s^a\) ：s状态下a动作的奖励值
    • \(P_{ss'}^a\) ：状态转移概率
    • \(\gamma\) ：折扣函数

  • 相关数学表达式：

    • 期望奖励函数 $R_s^a = E [R_{t+1} | S_t = s, A_t = a] $

    • 转移概率函数 \(P_{ss'}^a = P[S_{t+1} = s' | S_t = s,A_t = a]\)

    • 行为策略 \(\pi\) ：从状态空间 \(S\) 到动作空间 \(A\) 的映射

      \[\pi (a|s)=P[A_t = a | S_t = s] \]

      则状态转移概率函数和奖励函数可以重新定义为：

      \[P_{ss'}^{\pi} = \sum_{a∈A} \pi (a|s) P_{ss'}^a \]
      \[R_s^{\pi} = \sum_{a∈A} \pi (a|s) R_s^a \]

      当一个策略 \(\pi\) 的语气收益均大于其他策略的预期收益时，我们将策略 \(\pi\) 称之为最优策略（可能存在多个），表示为：

      \(Q^* (s,a) = \max E_{\pi} [R_t | S_t = s,A_t = a]\) （最优价值函数）

      它遵循Bellman最有方程：

      \[Q^* (s,a) = E_{s→s'} [r + \gamma \max_{a'} Q_i (s',a') | s,a] \]

Q-learning算法

算法描述参考上一篇博客

• Q-learning算法的几个特点
  • 一种探索加利用的学习方式，对先验知识不做要求或有较少的要求；
  • 采用增量的方法，是在线的学习方式；
  • 适用于在不确定的环境中学习；
  • 算法的体系结构可扩展；
  • 是收敛的算法。