学习日志-2021.09.25
学习日志-2021.09.25
今日进展（笔记）
-
Q-learning（基于值的算法）
-
使用了时间差分法（融合了蒙特卡洛和动态规划）能够进行off-policy的学习
-
算法描述:
-
初始化 Q = {}
-
while Q 未收敛:
- 初始化状态S，开始新一轮的游戏
- while S!=结束:
- 使用策略\(π\)，获得动作\(a=π(S)\)
- 使用动作\(a\)进行游戏，获得新的状态\(S'\)，与奖励\(R(S,a)\)
- \(Q[S,A] ← (1-\alpha)*Q[S,A]+\alpha*\{R(S,a)+\gamma*max_aQ[S',a]\}\) //更新Q
- \(S ← S'\)
-
使用策略\(\pi\),获得动作\(a=\pi(S)\)，该策略是根据Q表格来选择效用最大的动作，但这样的选择可能会使Q陷入局部最优，可以改进为\({\epsilon}-greedy\)方法（每个状态以\(\epsilon\)的概率进行探索，此时将随机选择动作，而剩下的1-\({\epsilon}\)的概率则进行开发）
-
更新Q表格
Q表根据如下公式进行更新：
\[Q[S,A] ← (1-\alpha)*Q[S,A]+\alpha*\{R(S,a)+\gamma*max_aQ[S',a]\} \]其中\(\alpha\)为学习速率，\(\gamma\)为折扣因子
学习速率\(\alpha\)越大，保留之前训练的效果就越少
\(R(S,a)\)指的是眼前的利益，\(max_aQ[S',a]\)指的是记忆中的利益
折扣因子\(\gamma\)越大，\(max_aQ[S',a]S\)所起到的作用就越大，即越重视以往的经验，\(\gamma\)越小，则注重眼前的利益。
-
-
-
机器学习
-
误差
- 经验误差（训练误差）：学习器在训练集上的误差
- 泛化误差：在新样本群上的误差
当学习器把训练样本学得太好了的时候，很可能已经把训练样本自身的一些特点当作潜在样本都具有的一般本质，这会导致泛化性能下降，这种现象称为“过拟合”
与“过拟合”相对的是“欠拟合”，指的是对训练样本的一般性质尚未学好。
-
评估方法（如何获得测试结果？）
测试集应该尽可能与训练集互斥，即测试样本尽量不在训练集中出现、未在训练过程中使用过。
-
留出法
- 直接将数据集D划分为两个互斥的集合，其中一个作为训练集S，另一个作为测试集T，一般训练集S占大部分。
- 使用留出法时，一般要采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果。
-
交叉验证法
- 交叉验证法线将数据集D划分为k个大小相似的互斥子集，即\(D = D_1∪D_2∪...∪D_k,D_i∩D_j=Φ(i≠j)\)。每个子集\(D_i\)都尽可能保持数据分布的一致性，即从\(D\)中通过分层采样得到。每次使用\(k-1\)个子集作的并集作为训练集，余下的那个子集作为测试集。
- 为减小样本划分不同而引入的差别，\(k\)折交叉验证通常要随机使用不同的划分重复\(p\)次，最终的评估结果是这\(p\)次\(k\)折交叉验证结果的均值。
-
自助法
-
给定\(m\)个样本的数据集\(D\)，我们对它进行采样产生数据集\(D'\)：每次随机从\(D\)中挑选一个样本，将其拷贝放入\(D'\)，然后再将该样本放回初始数据集中，使得该样本在下次采样时仍有可能被采到；这个过程重复执行\(m\)次后，我们就得到了包含\(m\)个样本的数据集\(D’\)，这就是自助采样的结果
样本在\(m\)次采样始终不被采到的概率是\(\lim_{m \to \infty} (1-\frac{1}{m})^m = \frac{1}{e}≈0.368\)，即初始数据集\(D\)中有36.8%的样本未出现在采样数据集\(D'\)中，我们可以采用\(D'\)用作训练集，\(D-D’\)用作测试集。
-
自助法在数据集较小、难以划分有效训练/测试集是很有用。自助法产生的数据集改变了初始数据集的分布，这回引入估计偏差。因此，在初始数据量足够时，留出法和交叉验证法更常用一些。
-
-
调参与最终模型
- 大多数学习算法都有些参数需要设定(超参数)。在进行模型评估与选择时，除了要对适用学习算法进行选择，还需要对算法参数进行设定。
- 参数调得好不好对性能往往对最终性能有关键影响。
-
-
性能度量（如何评估性能优势？）
衡量模型泛化能力的标准
模型的好坏是相对的，什么样的模型是好的，不仅取决于算法和数据，还取决于任务需求。
回归任务常用的性能度量是均方误差
$$ E(f;D) = \frac{1}{m} \sum_{i+1}^m (f(x_i)-y_i)^2 $$
更一般的，对于数据分布\(D\)和概率密度函数\(p(·)\)，均方误差可描述为
$$E(f;D)=\int_{x~D}(f(x_i)-y_i)^{2}p(x)dx$$
-
查准率、查全率与F1
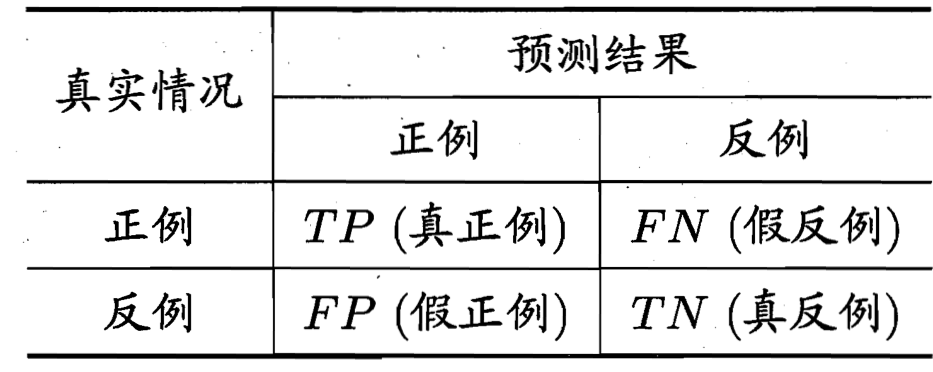
查准率：\(P=\frac{TP}{TP+FP}\),预测为正例的事件中，真正例的占比。
查全率：\(R=\frac{TP}{TP+FN}\),实际为正例的样例中，被判定为真正例的占比。
一般来说，查准率高时，查全率往往偏低；而查全率高时，查准率往往偏低。
-
在很多情形下，我们可以根据学习器的预测结果对样例进行排序，排在最前面的是学习器认为“最可能”是正例的样本，排在最后的则是学习器认为“最不可能”是正例的样本。按此顺序逐个把样本作为正例进行预测，每次可以计算出当前的查全率、查准率，得到“P-R曲线”。
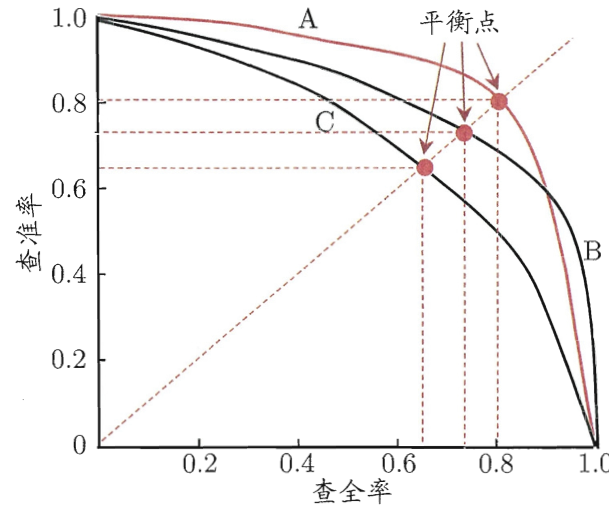
若一个学习器的P-R曲线被另一个学习器的曲线完全“包住”，则可断言后者性能优于前者(如图，A优于C，B也优于C，A、B之间则无法判断）。
平衡点（BEP）指的是“查准率=查全率”时的取值，是一个性能度量（A优于B优于C）。
BEP还是过于简化了些，更常用的是F1度量：
$$F1=\frac{2×P×R}{P+R}=\frac{2×TP}{样例总数+TP-TN}$$
F1度量的一般形式——\(F_\beta\),能让我们表达出对查准率/查全率的不同偏好
$$F_\beta=\frac{(1+\beta^2)×P×R} {(\beta^2×P)+R}$$
其中\(\beta>0\)度量了查全率对查准率的相对重要性。\(\beta=1\)是退化为标准的F1；\(\beta>1\)是查全率有更大影响；\(\beta<1\)时查准率有更大影响。
-
-
-
