使用查找表的SR-LUT实用单图像超分辨率(SR-LUT Practical Single-Image Super-Resolution Using Look-Up Table)
一篇入选CVPR2021会议的文章。该文章将神经网络的推理过程用查找表进行替代,从而减少运算开销。为了实现这一替代,在实现过程中运用了很多巧妙的处理技巧,算法与硬件的配合令人激动。
本文章主要包含:
- 我在学习中对英文原文的摘抄与翻译。
- 作为一个准研究生满怀好奇的碎碎念。
- 一点相关的小笔记。
复现进行中... ...
0. 摘要
随着移动的设备和显示硬件的发展,对实用SR技术的需求已经增加。当前最先进的SR方法是基于DNN以获得更好的质量。然而,它们在通过使用并行计算模块(例如GPU)执行时是可行的,并且难以应用于诸如终端用户软件、智能电话和电视机的一般用途。我们用小感受野训练深度SR网络,并将学习的深度模型的输出值传递到LUT。在测试时,我们从查询LR输入像素的LUT中检索预先计算的HR输出值。由于不需要大量的浮点运算,因此所提出的方法可以非常快地执行。实验结果表明了该方法的有效性和实用性。特别是,我们的方法运行速度更快,同时显示出更好的质量相比,双三次插值。
特点:比双三次插值效果更好,并且有更高的执行速度-可以看出以存储为代价来减少计算时间。
1. 引言
单幅图像超分辨率(SR)的目标是从对应的低分辨率(LR)输入图像生成具有足够高频细节的高分辨率(HR)结果。基于插值的方法在早期占主导地位,其中丢失的像素值通过具有已知值的附近像素的加权平均来估计。基于插值的方法的一些示例包括双线性、双三次[19]和Lanczos。该方法直观、快速,但是由于无论图像结构如何都应用相同的插值权重,因此它们很难恢复丢失的细节。结果,基于插值的SR的结果看起来过于模糊。
阐述了插值方法的感受域小,难以恢复细节的特点。其实也不完全正确,本文的感受域也不大,我们可以怀疑是连续与可导连续这样的假设出现了问题。
为了创建具有更好质量的HR图像,已经提出了多种方法。基于示例的方法利用从多个外部训练图像生成的LR-HR图像块对的数据库[3,11,10],或者利用来自测试图像本身的自相似性[12,47]。一个缺点是搜索最近邻面片非常耗时[5]。基于稀疏编码的方法[48,50,42,43],其学习面片的紧凑表示,也已经流行并且显示出有前景的结果。然而,计算输入面片的稀疏表示需要高计算成本。
在这里提出了查表方法和使用图片相似性进行分析的方法。
随着深度学习在各种计算机视觉任务中表现出强大的功能,将深度神经网络(DNN)用于SR的尝试激增[8,20,9,22,26,2,13,53,52,44,25,36,31,33]。它们在峰值信噪比(PSNR)方面实现了最先进的SR性能,然而,它伴随着来自众多卷积层的大量乘法运算。因此,图形处理单元(GPU)或张量处理单元(TPU)等专用并行计算设备对于处理高计算复杂度和存储器消耗至关重要。基于DNN的解决方案在没有专用硬件的情况下很难应用于实际,这是目前解决问题的主要方法之一。
在这里提出了神经网络对于硬件的局限性。
尽管出现了各种各样的SR算法,但基于插值的SR算法由于其简单实用,仍然被Photoshop、Matlab、OpenCV等图像处理软件普遍用作基础算法。尽管已经做出了很多努力来改善SR的视觉质量,但是相对较少考虑实际SR应用于具有有限数量的计算单元的终端用户软件和硬件(如消费者相机、监视相机、移动的电话和电视)中的可行性。最近,在移动的设备上运行深度模型变得越来越实用,这要归功于GPU附加的移动处理器和许多优化工作[16]。尽管如此,作为另一个研究方向,当GPU不可用时,为更一般的情况开发实用的方法是很重要的。
为此,我们提出了一种实用的单图像SR方法,它运行速度更快或与双三次插值相比,同时实现了更好的质量。我们采用了查找表(LUT)的方法,这是通常用于嵌入式系统,以加快计算。对于一个复杂的函数或一系列计算,如果我们计算一次输出值并将其放入LUT中,那么之后我们需要做的只是检索这些值,而不需要再次执行计算。因此,当计算时间比存储器访问时间长得多时,LUT是有效的。在图像处理中,LUT由于其卓越性而长期用于各种颜色传输任务和国际颜色联盟的标准配置文件中[34]。此外,由于LUT的硬件友好特性,其已被用于相机成像流水线[17]。类似地,LUT可以通过仅从存储器检索预先计算的输出来加速SR算法的总体运行时间,因为一系列浮点操作比存储器访问慢得多。
在这里说明了这种方法核心手段是查表,并且在查表这一技术手段已经十分成熟,已经有了大量优化支持。
在这篇文章中,我们训练深网络在某些约束学习深度模型的输出值映射到附近地区。我们限制接受域(RF)深度SR网络尽可能小(甚至到4像素)。通过小的感受域,我们可以计算出所有可能的学习网络的输出值作为输出值是决定只根据少量的输入值。训练后,输出值保存到的查找表(达到4D的查找表,大小与感受域相同)。我们的名字建立SR-LUT附近地区。
在这里点破了设计的内容-建立感受域与推测值之间的关系。
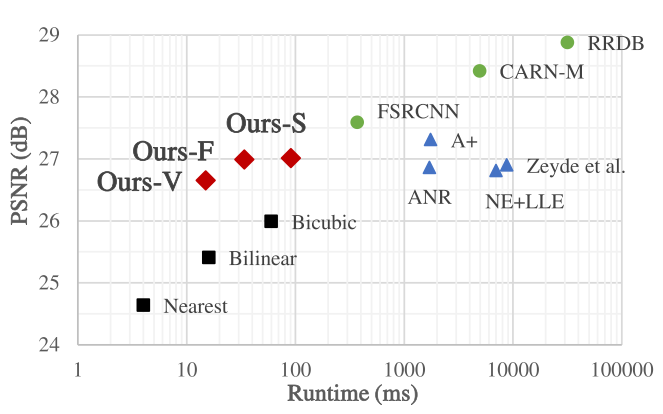
在图1中,我们将我们的方法与几种SR方法进行了比较。与双三次插值相比,我们的RF大小为2和3的非常快和快速模型(分别为Ours-V和Ours-F)运行得更快,而我们的RF大小为4的慢速模型(Ours-S)运行的时间相当,并且我们所有的模型都实现了更好的PSNR值。而且,我们的方法具有可比的PSNR值,并且比基于稀疏编码的方法(triangle)具有更快的速度。尽管基于深度学习的方法(circle)显然实现了更好的准确性,但它们难以实现超过一定水平的更快运行时间,限制了它们的实际使用。
总之,本文的贡献是:
- 通过将输入和输出值从学习的深度SR模型转移到查找表(SRLUT)中,我们介绍了一种快速实用的单幅图像SR的简单新颖方法。据我们所知,这是第一次展示LUT在单幅图像SR中的优势。
- 我们的方法本质上更快,因为我们只是从存储器上的LUT中检索预先计算的值,而不是像以前的SR方法那样执行由大量浮点乘法和加法运算组成的繁重计算。我们在智能手机上的实验中验证了我们方法的有效性,并且我们的快速模型比双三次插值运行得更快。
- 我们的方法可以很容易地在软件和硬件上实现为存储器阵列,而不需要特殊的计算模块,如GPU。我们相信这一优点将使我们的方法能够用于各种实际的SR应用。
我们可以认为,对应关系仍然是用深度学习建立(也就是训练过程仍然是深度学习),但是推理过程从神经网络计算变成了查表。因此改研究将重心放在了如何简化推理过程之上。
2. 相关工作
2.1. 快速超分辨率
由于基于稀疏编码的方法表现出良好的SR性能[48,50,4],因此已经引入了用于更快地运行这些方法的若干方法。在ANR [42]和A+ [43]中,作者预先从学习的稀疏字典中计算了投影矩阵,该矩阵将LR输入特征映射到HR输出面片。在测试时,通过使用预先计算的投影矩阵来获得HR输出。这种方法将速度提高到基线方法的5-10倍[50]。具体来说,ANR需要超过一秒的时间从我们的台式计算机(英特尔至强CPU E31230 v3@3.30GHz,32 GB RAM)上的320×180输入图像生成1280×720输出图像。
RAISR [37]为SR任务学习了一组滤波器,计算复杂度较低,运行时间比以前的工作更快。然而,该方法不如内插快,因为该方法针对哈希表密钥计算输入图像的每个面片的图像梯度和奇异值分解。此外,还存在其他类型的快速SR方法[35,38,41]。
虽然有快速SR的努力,但与几乎在恒定时间内执行的双三次插值相比,这些方法仍然需要很长的时间。相比之下,我们基于LUT的方法本质上比上述方法更快因为它只需要非常少的计算来产生输出。如图1所示,我们的方法在移动设备上运行得比双三次插值更快或一样快。注意,结合DNN和LUT以提高效率的研究已经出现,例如在光增强[49]中。
2.2. 实时深超分辨率
基于GPU深度学习的实时SR算法也已被提出。在早期基于DNN的SR工作中,通过使用少量卷积层来实现更快的运行时间。ESPCN [39]和FSRCNN [9]分别使用了3层和8层卷积层,特征维数较小。但是,使用较小的模型容量很难实现最先进的性能。
这里使用的SR算法是深度学习算法。
以下研究集中于减少大型模型,同时最大限度地降低性能下降[15,51,28]。CARN-M [2]通过用群卷积代替传统的卷积,减少了其原始大模型CARN的参数数目和乘加运算。PAMS [24]将原始全精度32位SR模型量化为8位或4位以进行模型压缩。BSRN [46]进一步将原始模型量化为二进制精度。此外,FALSR [7]、ESRN [40]和TPSR [23]采用神经架构搜索算法从给定的高效卷积构建块中快速准确地找到轻量级深度SR网络。
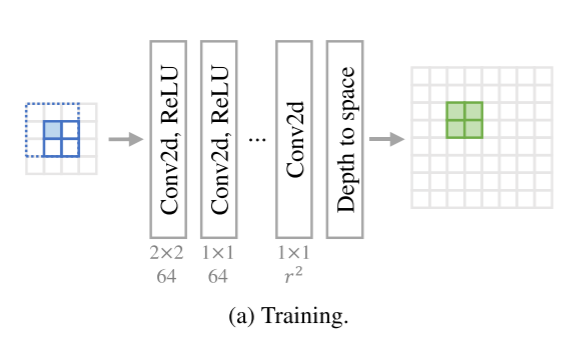
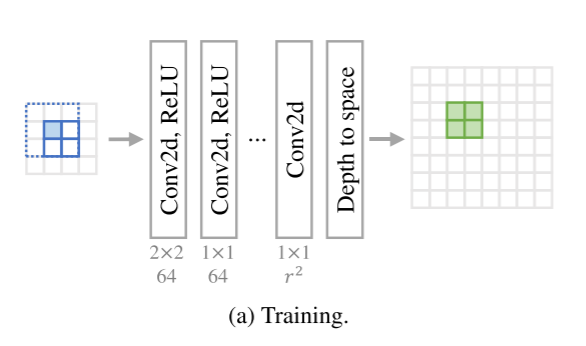
通过构建轻量级神经网络以优化训练过程。由图可得,在训练的时候使用一个像素点复原了四个像素点。其感知域是蓝色2x2区域。
测试是将图像输入训练好的SR-LUT,得到超分辨率的图像。再将得到的图像与原始图像进行对比。
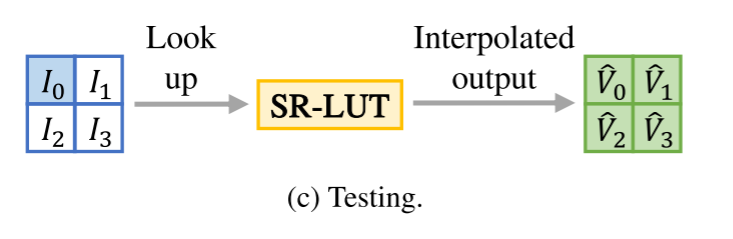
将对应关系进行存储,其中包含四个维度的采集样本索引,两个维度的图像长与宽的索引。
这里有一些想法,在深度学习中卷积核并不受长和宽的影响,因此为什么超分辨率的时候会考虑长与宽的影响呢?我们应该将更多的存储空间放在输入与输出的对应关系的规模上,例如输入的感受域为5x5,输出为3x3。
正如我们所看到的,人们已经为实现SR做出了各种努力。一些方法在CPU上实时执行,然而,没有一种方法是针对在有限的计算资源(如移动的设备)上运行的。因为它们由卷积层组成,需要良好的浮点乘法和加法运算的数量,在计算资源有限的设备中,运行时间将增加。实际上,FSRCNN在我们的桌面上需要77毫秒,在三星Galaxy S7智能手机上需要371毫秒。相比之下,我们提出的SR-LUT不需要这样的计算开销,我们的快速模型在智能手机上只需34毫秒,而性能不会下降太多。对于计算能力较低、深度方法难以应用的器件,该方法是一种合适的选择。
使用计算得到的输入与输出的映射关系,是连续的对应关系。而使用查找得到的输入与输出的对应关系是离散的对应关系。因此我认为这是一种很极端的做法,参数化的运算得到的映射关系需要更多的计算步骤,但是使用的内存更小。
3. 方法
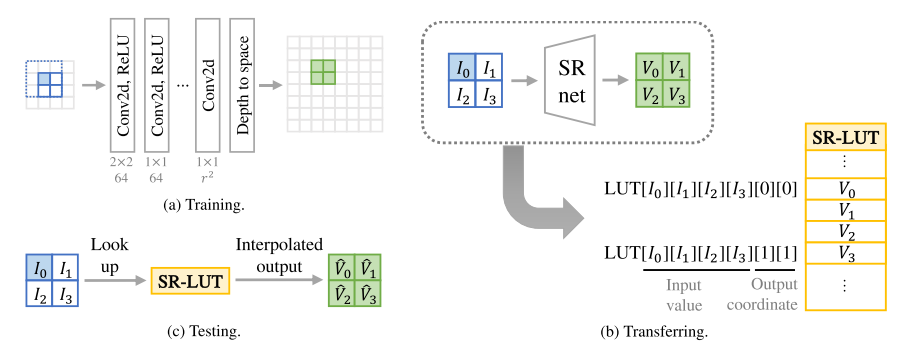
我们的方法概述如图2所示。为了获得SR-LUT,我们首先训练一个具有小RF尺寸的轻量级深度SR网络(图2a),并将深度模型的输出值转移到SR-LUT(图2b)。在测试时,对于输入LR面片,从SR-LUT中获得相应的HR像素值(图2c)。
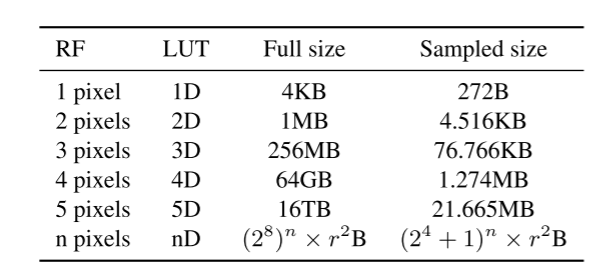
对于实际的SR-LUT,深度模型的RF大小应当较小,因为SR-LUT的大小随着RF大小的增加而指数地增加。注意,由于可能的输入和输出值的范围太大,因此很难利用现有的深度模型来进行LUT。在表1中,我们估计了在存储8位输入和输出值时用于上缩放因子r的SR-LUT的大小。例如,当RF大小为2且r = 4时,完整LUT大小计算为(28)2 × 42 × 8位= 1 MB,因为需要(28)2个LUT条目(8位输入值为28个bin),每个条目有42个8位输出值。类似地,当RF大小为3、4和5个像素时,完整SR-LUT占用256 MB、64 GB和16 TB存储空间。因为当RF大小大于或等于3时,完整SR-LUT大小太大,所以在实践中我们使用采样LUT。我们经验性地发现,RF大小对于实际实现应当小于或等于4个像素,因为它影响运行时间。我们将我们的V、F和S的RF大小分别设置为2、3和4。我们的-V和我们的-F比我们的-S快,但我们的-S的视觉质量更好。本节以下内容将基于具有2 × 2卷积核的RF尺寸4(Ours-S配置)进行说明,但其他RF尺寸也适用。由于RF大小有限,每个颜色通道必须独立处理。
3.1. 训练深度SR网络
网络架构由于网络受限于非常小的RF大小,大量卷积层不会无限地提高精度,而是收敛得更快。因此,我们使用了一个由6个卷积层组成的深度网络,除了最后一层之外,后面都是ReLU激活(图2a)。对于RF大小4,第一层的内核大小设置为2 × 2,其余层的内核大小设置为1 × 1。第一层可以使用不同的内核形状(例如1 × 4)。然而,2 × 2形状是最合适的,因为它考虑了最相关的4个相邻输入像素,并且它在实验中显示出更好的视觉质量(第第4.3节)。卷积层中的特征数被设置为64,并且最后一层的特征数被设置为r2。通过空间深度操作[39]将网络的输出斑点整形为期望的大小。我们注意到,层数不影响最终运行时间,因为深度模型仅用于构建对应的SR-LUT。
旋转集合训练 通常,当考虑更多的像素时,SR任务的性能可以得到改善。但是,我们的RF尺寸4(2 × 2)太小,无法准确估计HR图像。例如,FSRCNN [9]的RF大小是169个像素(13×13),甚至双三次插值也利用16个(4 × 4)最近邻像素。
为了利用LR输入中的更多区域,我们在训练阶段使用旋转系综。对于我们的深层网络,0、90、180和270度的4个旋转系综覆盖了总共9(3 × 3)个LR像素(图2a中蓝色虚线区域相对于蓝色参考像素)。将来自4次旋转的每个输出相加以生成最终输出。形式上,最终输出yi可以表示为:
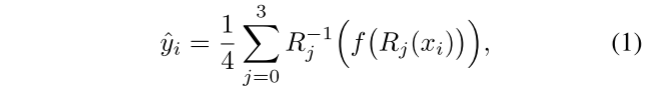
其中xi是LR输入面片,f是深度SR网络,Rj是图像旋转到j ×90度的操作,R−1 j是反向旋转操作。SR网络f通过使用像素重构损失来训练:
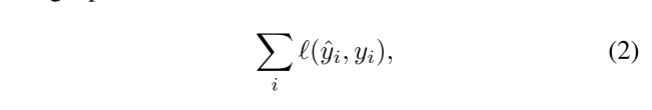
其中yi是GT目标面片,是均方误差。
从旋转这个操作可以看出来,图片从低分辨率到高分辨率不应该受到方向的影响。从公式可以看出,可以使用矩阵乘积的形式来进行矩阵的旋转,并且给予每个方向相同的权重。
旋转自系综策略在以前仅在测试时用于的深层SR最大化准确度[26,52]工作中。我们在训练时进一步应用该策略,以在具有小RF尺寸的同时提高性能。这对于我们的方向核形状非常有效,有助于实现良好的效果。即使RF与其他SR方法相比太小,我们也可以通过该策略有效地考虑更多的面积来进行精确SR而不增加LUT大小
3.2. 传输至LUT
训练深度SR网络后,我们为RF尺寸4构建了4D SRLUT(图2b)。注意,图2b示出了6D LUT,但是通过仅考虑输入值维度,我们将其称为4D LUT。对于完整的LUT,我们针对所有可能的输入值计算学习的深度网络的输出值,并将它们保存到LUT。输入值用作LUT的索引,相应的输出值存储在该位置。在实践中,我们使用均匀采样的LUT,因为完整LUT的大小非常大(64GB)。具体地,我们将2^8个bin(对于8位输入图像为0 - 255)的原始输入空间均匀地划分为2^4 + 1个bin。换句话说,我们通过以2^4的采样间隔大小相等地间隔原始输入空间来采样点。结果,均匀采样的4D SRLUT在输入点0、16、......240和255(最后一个点),并且大小减小到1.274MB(4D LUT [256][256][256]减小到LUT [17][17][17][17])。在测试时,未采样点的值通过使用最近采样点的值进行插值。我们已经测试了从22到28的采样间隔范围,并验证了在实验中直到间隔大小为24时,原始性能几乎保持不变(第第4.3节)。
通过降低输出结果的分辨率(也就是降低准确性),来达到减少储存空间的效果。
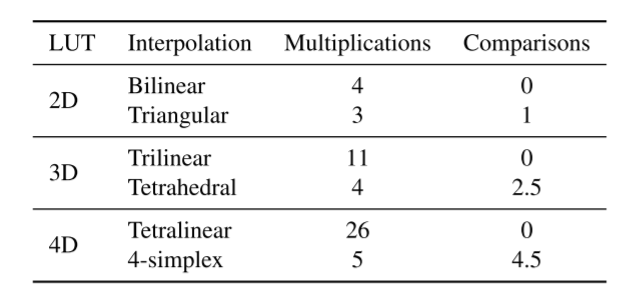
表2.多维LUT的线性插值和四面体插值等价物的乘法和比较操作的数目。我们使用后一种方法,因为它实际上需要更快的运行时间。
为了获得更好的精度,在颜色传输任务中经常使用非均匀采样技术[27,32]。然而,由于它们需要额外的计算和比较来定位最近采样点的索引,因此总体运行时间增加。这与我们的快速和实用SR方法的目标形成对比。因此,我们使用均匀采样以便于实现和更快的运行时间。
3.3. 使用SR-LUT进行测试
一旦SR-LUT构建完成,SR将仅使用SR-LUT执行(图2c)。在使用完整LUT的情况下,直接从LUT检索输出HR值。另一方面,在使用采样LUT的情况下,需要适当的插值技术以通过使用最近采样点的值来生成输出值。为了索引最近的采样点,我们简单地取输入像素值的最高有效位(MSB),因为我们使用等采样LUT。这可以通过屏蔽和移位位来实现。对于8位输入像素值,我们取4个MSB,然后定位最近的采样点之一。
为了内插找到的最近采样点的值,可以使用线性内插作为基线方法。即,分别用于2D、3D、4D和5D SR-LUT的双线性、三线性、四线性和五线性内插。相反,我们使用众所周知的四面体插值方法[18],因为它比3D LUT的三线性插值更快。四面体插值计算3D空间中四面体的边界4个顶点的值的加权和。在表2中,我们比较了多维LUT的线性内插和四面体内插等价物的操作数量。对于3D LUT,三线性插值需要至少11次乘法,而四面体插值仅需要4次乘法和2.5次比较操作(if-else)。在实践中,四面体插值(包括比较操作)的总体运行时间比三线性插值快[18],其他维度也是如此。
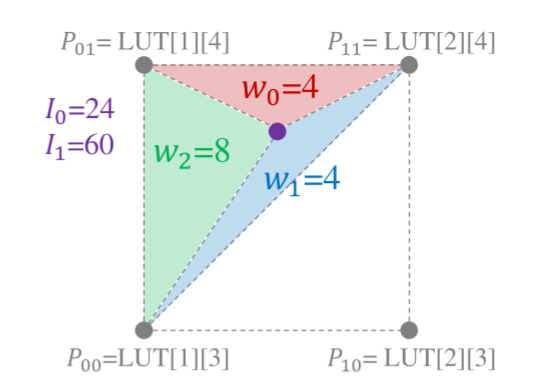
表3.4D空间的四面体插值等效(4-单纯形内的插值)。根据输入值的LSB的值,总共存在24种情况。
面插值,我们解释了二维等效三角插值图3。对于查询输入I0 = 24(00011000(2))和I1 = 60(00111100(2)),我们首先将输入值拆分为4个MSB和4个最低有效位(LSB)。I0和I1的MSB值分别为1和3,用于确定最近的采样点。LSB的值,分别对于I0和I1的Lx = 8和Ly = 12,用于确定边界三角形和边界顶点的权重。两个边界顶点固定在P00 = LUT[1][3]和P11 = LUT[1+1][3+1],另一个顶点通过比较Lx和Ly。在本例中,由于Lx<Ly,因此选择P01 = LUT[1][3 + 1],否则选择P10(为简单起见,我们省略输出值坐标)。每个顶点的权重是相对三角形的面积,计算公式为w0 = W − Ly,w1 = Ly − Lx,w2 = Lx,其中W = 24(采样间隔)。最后,输出值计算为加权和,如下所示:V =(w0 P00+w1 P01+w2 P02)/W。
同样地,四面体插值可以通过使用4-单纯形几何的边界5个顶点的值而扩展到4D空间。取决于LSB的值(分别用于I 0、I1、I2和I3的Lx、Ly、Lz、Lt),在总共24种情况中选择一个4-单纯形。在表3中,我们示出了每种情况的权重wi和边界顶点Oi。然后,输出值计算为加权和,如下所示:
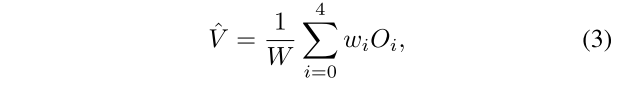
其中O0 = P0000,O4 = P1111。
我们也可以将相同的方法应用于5D LUT。在5维单纯形几何中插值只需6次乘法。然而,总案例数增加到120,我们根据经验发现这会影响运行时间。因此,我们将最大RF大小设置为4。
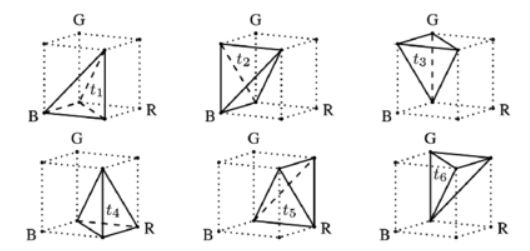
四面体插值 tetrahedral:
四面体插值将立方体分成t1~t6共六个部分,如果被插值的点位于t1,则只使用t1的4个顶点做插值,其它四面体同理。相比金字塔插值,参与计算的顶点距离被插值点更近,效果会更好,但判定被插值点所属四面体的过程也更复杂。
下表总结了各种插值方法的计算复杂度。

4.实验
4.1. 实验设置
对于训练,我们使用在深度SR方法中广泛使用的DIV 2K [1]数据集。DIV 2K数据集包含800张2K分辨率的训练图像,涵盖了从城市景观到自然景观的各种内容。在实验中,我们将放大因子固定为4(即r = 4)。我们的SR深度模型使用Adam优化器[21]进行了2×105次迭代训练,学习率为10−4,小批量大小为32。训练完成后,我们将学习的深度模型的输出值传输到SR-LUT。1
为了进行测试,我们使用了在单幅图像SR任务评估中广泛使用的5个常见测试集——Set 5、Set 14、BSDS 100 [29]、Urban 100 [14]和Manga 109 [30]。对于定量评估,我们使用传统上用于图像质量评估的PSNR和结构相似性指数(SSIM)[45]。此外,我们还在三星Galaxy S7智能手机上测试了每种方法的运行时间,以验证其真实的应用的可行性。
PSNR (Peak Signal-to-Noise Ratio) 峰值信噪比:
给定一个大小为MxN的干净图像I和噪声图像K,均方误差定义(MSE)为:
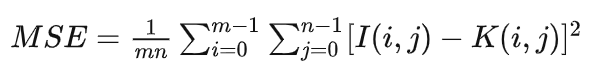
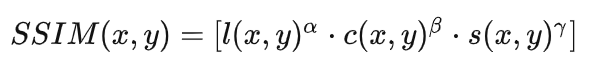
我们比较了我们的方法与各种单图像SR方法从插值到DNN的方法。我们选择了3种基于插值的方法-最近邻、双线性和双三次插值,4种基于稀疏编码的方法- NE + LLE [6]、Zeyde等人[50]、ANR [42]和A+ [43],以及3种基于DNN的方法- FSRCNN [9]、CARN-M [2]和RRDB [44]。注意,所有基于稀疏编码的方法使用在[50]中学习的相同字典。FSRCNN是最快的深度单幅图像SR模型之一,CARN-M是平衡速度和精度的模型,而RRDB是表现出最佳精度的模型。
定量结果见表4。我们的-V、我们的-F和我们的-S分别使用2D全LUT、3D采样LUT和4D采样LUT。测量从320 × 180输入生成1280 × 720输出RGB图像的运行时间,测量10次,然后取平均值。我们使用Pytorch在智能手机上实现基于DNN的方法。然而,基于稀疏编码的方法很难在智能手机上实现。基于稀疏编码的方法的运行时间是通过使用Matlab在配备Intel Xeon E3-1230 v3 CPU和32 GB RAM的台式计算机上测量的,如果在智能手机上执行,可能会更差。该方法的一个重要优点是查找表的实现不需要任何特殊的框架,如Matlab或Pytorch,这使得该方法易于在软件和硬件上实现。
函数的本质就是对应关系的存在,神经网络的运行也是依托网络来进行对应关系的表达。但是网络通过计算结构的表达降低了内存而增加了运算量。
与双三次插值相比,我们的 -V 实现了更快的运行时间(-45ms)和更好的PSNR和SSIM值,并具有良好的裕度(Set5测试集分别为+0.8dB和+0.0203)。类似地,我们的 -F 也运行得更快(-26ms),并显示出相当大的性能差距(集5为+1.35dB和+0.0328)。我们的S需要多一点的运行时间(+31ms),但在我们的模型中显示出最好的视觉质量。与基于稀疏编码的方法相比,我们的结果显示了更好的PSNR和SSIM性能,同时具有比它们的字典更小的LUT,除了A+。A+显示出比 我们的-S更好的PSNR和SSIM值(对于集合5为+0.45dB和+0.0124),然而,我们的-S运行更快,并且占用的存储器空间大约小12倍。基于DNN的方法显示了最先进的PSNR和SSIM,但需要较长的运行时间。FSRCNN显示出与我们的方法相比的性能差距(对于集合5,比我们的S好+0.89dB和+0.0178),但显示出分别比我们的S、我们的F和我们的V慢4、11和25倍的运行时间。综上所述,我们验证了快速的运行时间与中等准确性的实际使用,因为我们的方法在理论上有更少的计算开销。
目视比较见图4。我们展示了自然纹理、文本和人工结构的3幅图像。对于前两行,我们的 -V 和我们的 -F 结果显示了由于有限的RF尺寸导致的一些伪影。对于最后一行,我们的F结果看起来部分优于我们的S。这是因为我们的 -V 和我们的 -F(分别为1×2和1×3)的核形状可以在水平和垂直方向上考虑更多的像素,而我们的 -S(2 × 2)的核可以对角地考虑像素。与双三次插值相比,我们的结果通常看起来更清晰。在某些示例中,Ours-S显示比A+(第二行)更高的清晰度,并且显示出与FSRCNN(第一行)相似的锐度水平。请参阅补充资料以了解更多结果。
表4.5种常见单幅图像SR测试集(r = 4)的定量比较。在我们的型号中,最佳值以粗体显示。我们的V和F比双三次插值更快,并获得了更好的PSNR和SSIM值,具有良好的裕度。我们的S速度较慢,但显示出更好的视觉质量。在Samsung Galaxy S7智能手机上测量生成1280 × 720输出图像的运行时间。* :运行时间在桌面上测量。†:DNN的参数个数。
在这个表可以看出 -V -S 以及 -F 模型在精度之间比较 -S 并没有绝对的优势。在这种模型下,改变感受域并没有带来绝对的提升(-S 的精度表现在有的数据集表现良好,在有的数据集表现不理想)。我们仍然需要对数据集进行分析,确定不同数据集上训练应该使用怎样的模型。

图4.图像质量结果。我们所有的结果显示,提高锐度相比,双三次插值。我们的S显示了我们的模型中最好的视觉质量,具有平滑的边缘,特别是对角方向。
4.3. 分析
RF尺寸和核形状实验在我们的方法的各种配置上进行以分析RF尺寸的影响。我们测试了2到4个射频尺寸,第5组测试集的详细配置和结果如表5所示。RF大小为2,核为1 × 2(我们的 -V),通过使用旋转系综总共使用5个输入像素。同样,RF尺寸为3,1 × 3内核(我们的 -F)覆盖9个,RF大小为4,内核为1 × 4(配置B),覆盖13个输入像素。RF尺寸越大,图像质量越好,但由于内插输出值的计算复杂度越高,因此需要的运行时间越长。从2D扩展到3D SR-LUT将运行时间增加19 ms,从3D扩展到4D SR-LUT将运行时间增加57 ms。同样,5D SR-LUT的运行时间将大得多,使得实际使用困难。对于实际实现,应当考虑精度和速度之间的折衷。
可以看出区分 -V -S 以及 -F的要素是感知域的大小。感知域越大,需要的查表元素越多存储空间越多,需要的计算量也急速增加。
我们还对不同的核形状进行了实验。配置A和我们的配置F具有相同的RF尺寸3,1 × 3核,但A具有旋转2次的对称核形状。我们的 -F 显示出比A好得多的PSNR和SSIM值,并且我们推断这是因为非对称核一次只需要关注单个方向信息。这似乎在我们非常小的感知尺寸设置中更明显。构型B和我们的构型S具有相同的RF尺寸4,但构型B和我们的构型S的核形状分别为1×4和2×2。它们在定量比较中表现出几乎相同的性能。然而,我们的 -S 显示了更令人满意的视觉结果,如图5所示,因为2 × 2内核考虑了最相关的4个相邻输入像素。此外,如果不应用旋转系综,则性能下降(Ours-S w/o RE)。
采样间隔这里,我们基于我们的-S模型对SR-LUT的采样间隔大小(bin大小)进行实验。增加采样点的数量会减小查找表的大小,但由于非采样点需要从采样点中插值,从而破坏了查找表的精度。表6总结了第5组测试集样本量为2^2 - 28的结果。对于采样大小23,LUT的大小从64 GB减小到18 MB,同时保持原始PSNR和SSIM值。当采样数为24时,查找表的大小大大减小到1.274MB,同时性能损失最小(PSNR和SSIM分别为-0.08dB和-0.0026)。因此,我们选择大小24作为Ours-V、Ours-F和Ours-S的默认设置。如果LUT大小很重要,则采样大小25和26可能是更好的选择。从采样大小26到2^8,我们应该注意使用,因为会出现明显的伪影,如图6所示。对于实际实现,再次地,应当考虑精度和尺寸之间的折衷。
伪影: 本不存在却出现在的影像片子上的一种成像。
(1)Ringing artifacts / Gibbs artifacts / Spectral leakage artifacts / truncation artifacts(振铃伪影):图像的灰度剧烈变化处产生的震荡,就好像钟被敲击后产生的空气震荡。振铃伪影通常出现在图像的锐利边缘附近以伪边缘形式出现。 They visually look like bands or "ghosts" near edges.如下图:

5.结语
提出了一种简单实用的基于查找表的单幅图像空间重构方法(SR-LUT)。我们的方法本质上更快,因为预先计算的HR值只是从SR-LUT中检索,并且对最终输出进行了一些计算。与双三次插值相比,我们的快速模型(Ours-V和Ours-F)运行速度更快,同时以良好的幅度实现更好的定量性能,而我们的慢速模型(Ours-S)显示出更好的视觉质量,运行时间稍长。我们相信我们的方法由于其速度快和易于实现而在实际应用中可能是优选的。未来,使用更大的RF尺寸来提高质量并加速插值步骤将使我们的方法更加实用。致谢本研究得到了韩国政府(MSIT)资助的信息与通信技术规划与评估研究所(IITP)赠款的支持(编号2014-3-00123,面向大规模实时数据分析的高性能可视化BigData发现平台的开发,以及编号2020-0-01361,人工智能研究生院项目(延世大学))。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号