POJ——T2446 Chessboard

http://poj.org/problem?id=2446

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 18560		Accepted: 5857

Description

Alice and Bob often play games on chessboard. One day, Alice draws a board with size M * N. She wants Bob to use a lot of cards with size 1 * 2 to cover the board. However, she thinks it too easy to bob, so she makes some holes on the board (as shown in the figure below). 

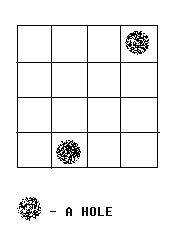
We call a grid, which doesn’t contain a hole, a normal grid. Bob has to follow the rules below: 
1. Any normal grid should be covered with exactly one card. 
2. One card should cover exactly 2 normal adjacent grids. 

Some examples are given in the figures below: 
 
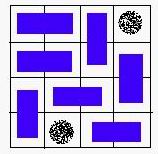
A VALID solution.
 
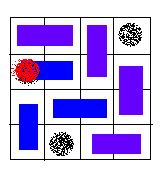
An invalid solution, because the hole of red color is covered with a card.
 
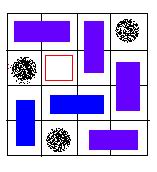
An invalid solution, because there exists a grid, which is not covered.
Your task is to help Bob to decide whether or not the chessboard can be covered according to the rules above.

Input

There are 3 integers in the first line: m, n, k (0 < m, n <= 32, 0 <= K < m * n), the number of rows, column and holes. In the next k lines, there is a pair of integers (x, y) in each line, which represents a hole in the y-th row, the x-th column.

Output

If the board can be covered, output "YES". Otherwise, output "NO".

Sample Input

4 3 2
2 1
3 3

Sample Output

YES

Hint

 
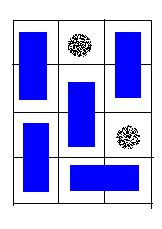
A possible solution for the sample input.

Source

POJ Monthly,charlescpp

 

题解：

把棋盘染成这个样子，有障碍的不染，用黑色格子与白色格子匹配，对这一个二分图求最大匹配。如果Ans*2+K=N*M,则能完全覆盖

 

#include <algorithm>
#include <cstring>
#include <cstdio>

using namespace std;

const int N(32*32);
int n,m,p,x,y,ans;
int match[N][N][2],lose[N][N];
int vis[N][N],sumvis;
int fx[4]={1,0,-1,0};
int fy[4]={0,1,0,-1};

bool DFS(int x,int y)
{
    for(int i=0;i<4;i++)
    {
        int xx=x+fx[i], yy=y+fy[i];
        if(vis[xx][yy]!=sumvis&&!lose[xx][yy])
        {
            vis[xx][yy]=sumvis;
            if(!match[xx][yy][0]||DFS(match[xx][yy][0],match[xx][yy][1]))
            {
                match[xx][yy][0]=x;
                match[xx][yy][1]=y;
                return true;
            }
        }
    }
    return false;
}

int main()
{
    while(~scanf("%d%d%d",&n,&m,&p))
    {
        if((n*m-p)%2)
        {
            printf("NO\n");
            continue;
        }
        ans=sumvis=0;
        memset(vis,0,sizeof(vis));
        memset(lose,0,sizeof(lose));
        memset(match,0,sizeof(match));
        for(int i=1;i<=p;i++)
        {
            scanf("%d%d",&x,&y);
            lose[y][x]=1;
        }
        for(int i=0;i<=n;i++) 
            lose[i][0]=lose[i][m+1]=1;
        for(int i=0;i<=m;i++) 
            lose[0][i]=lose[n+1][i]=1;
        for(int i=1;i<=n;i++)
          for(int j=1;j<=m;j++)
            if((i+j)%2==0&&!lose[i][j])
            {
                sumvis++;
                if(DFS(i,j)) ans++;
            }
        if(ans*2+p==m*n) printf("YES\n");
        else printf("NO\n");
    }
    return 0;
}