P1265 公路修建 洛谷

https://www.luogu.org/problem/show?pid=1265

题目描述

某国有n个城市，它们互相之间没有公路相通，因此交通十分不便。为解决这一“行路难”的问题，政府决定修建公路。修建公路的任务由各城市共同完成。

修建工程分若干轮完成。在每一轮中，每个城市选择一个与它最近的城市，申请修建通往该城市的公路。政府负责审批这些申请以决定是否同意修建。

政府审批的规则如下：

（1）如果两个或以上城市申请修建同一条公路，则让它们共同修建；

（2）如果三个或以上的城市申请修建的公路成环。如下图，A申请修建公路AB，B申请修建公路BC，C申请修建公路CA。则政府将否决其中最短的一条公路的修建申请；

（3）其他情况的申请一律同意。

一轮修建结束后，可能会有若干城市可以通过公路直接或间接相连。这些可以互相：连通的城市即组成“城市联盟”。在下一轮修建中，每个“城市联盟”将被看作一个城市，发挥一个城市的作用。

当所有城市被组合成一个“城市联盟”时，修建工程也就完成了。

你的任务是根据城市的分布和前面讲到的规则，计算出将要修建的公路总长度。

输入输出格式

输入格式：

 

第一行一个整数n，表示城市的数量。(n≤5000)

以下n行，每行两个整数x和y，表示一个城市的坐标。(-1000000≤x，y≤1000000)

 

输出格式：

 

一个实数，四舍五入保留两位小数，表示公路总长。（保证有惟一解）

 

输入输出样例

输入样例#1：
4
0 0
1 2
-1 2
0 4
输出样例#1：
6.47

说明

修建的公路如图所示：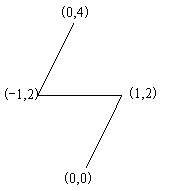

 

很容易发现，特殊情况没什么用，唬人的~~~、

 

表示我无奈的一zui代码~

 1 #include <algorithm>
 2 #include <iostream>
 3 #include <cstdio>
 4 #include <cmath>
 5 
 6 #define N 5233
 7 #define maxn 1e7
 8 
 9 using namespace std;
10 
11 int minn,k;
12 bool vis[N];
13 int n,x[N],y[N];
14 double d[N],ans;
15 double dis[N][N];
16 
17 void Prime()
18 {
19     for(int i=1;i<=n;i++) d[i]=dis[1][i];
20     d[1]=0;vis[1]=1;
21     for(int i=1;i<n;i++)
22     {
23         minn=maxn;
24         for(int j=1;j<=n;j++)
25             if(!vis[j]&&minn>d[j])
26             {
27                 minn=d[j];
28                 k=j;
29             }
30         vis[k]=1;
31         for(int j=1;j<=n;j++)
32             if(!vis[j]&&d[j]>dis[k][j])
33             d[j]=dis[k][j];
34     }
35 }
36 
37 int main()
38 {
39     scanf("%d",&n);
40     for(int i=1;i<=n;i++)
41         cin>>x[i]>>y[i];
42     for(int i=1;i<=n;i++)
43         for(int j=1;j<=n;j++)
44             dis[i][j]=sqrt(pow((x[i]-x[j]),2)*1.0+pow((y[i]-y[j]),2)*1.0);
45     Prime();
46     for(int i=1;i<=n;i++)
47         ans+=d[i];
48     printf("%.2lf",ans);
49     return 0;
50 }
80分，TLE两个（最朴素的Prime）
 1 #include <algorithm>
 2 #include <iostream>
 3 #include <cstdio>
 4 #include <cmath>
 5 
 6 #define N 5233
 7 #define maxn 1e7
 8 
 9 using namespace std;
10 
11 bool vis[N];
12 double minn;
13 double d[N],ans;
14 int n,x[N],y[N],k;
15 
16 double count(int i,int j)
17 {
18     return sqrt(pow((x[i]-x[j]),2)*1.0+pow((y[i]-y[j]),2)*1.0);
19 }
20 
21 int main()
22 {
23     scanf("%d",&n);
24     for(int i=1;i<=n;i++)
25         scanf("%d%d",&x[i],&y[i]);
26         
27     for(int i=2;i<=n;i++) d[i]=count(1,i);
28     d[1]=0;vis[1]=1;
29     for(int i=1;i<n;i++)
30     {
31         minn=maxn;
32         for(int j=1;j<=n;j++)
33             if(!vis[j]&&minn>d[j])
34             {
35                 minn=d[j];
36                 k=j;
37             }
38         vis[k]=1;ans+=minn;
39         for(int j=1;j<=n;j++)
40         {
41             double cnt=count(k,j);
42             if(!vis[j]&&d[j]>cnt)
43             d[j]=cnt;
44         }
45             
46     }
47     
48     printf("%.2lf",ans);
49     return 0;
50 }
80分，TLE两个（不用二维数组存图）
 1 #include <algorithm>
 2 #include <iostream>
 3 #include <cstdio>
 4 #include <cmath>
 5 
 6 #define N 5233
 7 #define maxn 1e7
 8 
 9 using namespace std;
10 
11 int minn,k;
12 bool vis[N];
13 int n,x[N],y[N];
14 double d[N],ans;
15 
16 double count(int i,int j)
17 {
18     return sqrt(pow((x[i]-x[j]),2)*1.0+pow((y[i]-y[j]),2)*1.0);
19 }
20 
21 void Prime()
22 {
23     for(int i=2;i<=n;i++) d[i]=count(1,i);
24     d[1]=0;vis[1]=1;
25     for(int i=1;i<n;i++)
26     {
27         minn=maxn;
28         for(int j=1;j<=n;j++)
29             if(!vis[j]&&minn>d[j])
30             {
31                 minn=d[j];
32                 k=j;
33             }
34         vis[k]=1;
35         for(int j=1;j<=n;j++)
36         {
37             double cnt=count(k,j);
38             if(!vis[j]&&d[j]>cnt)
39             d[j]=cnt;
40         }
41             
42     }
43 }
44 
45 int main()
46 {
47     scanf("%d",&n);
48     for(int i=1;i<=n;i++)
49         cin>>x[i]>>y[i];
50     Prime();
51     for(int i=1;i<=n;i++)
52         ans+=d[i];
53     printf("%.2lf",ans);
54     return 0;
55 }
90分，TLE一个（小优化）
 1 #include <algorithm>
 2 #include <iostream>
 3 #include <cstdio>
 4 #include <cmath>
 5 
 6 #define N 5233
 7 #define maxn 1e7
 8 
 9 using namespace std;
10 
11 bool vis[N];
12 double minn,cnt;
13 double d[N],ans;
14 int n,x[N],y[N],k;
15 
16 double count(int i,int j)
17 {
18     return sqrt((double)(x[i]-x[j])*(x[i]-x[j])+(double)(y[i]-y[j])*(y[i]-y[j]));
19 }
20 
21 int main()
22 {
23     scanf("%d",&n);
24     for(int i=1;i<=n;i++)
25         scanf("%d%d",&x[i],&y[i]);
26         
27     for(int i=2;i<=n;i++) d[i]=count(1,i);
28     d[1]=0;vis[1]=1;
29     for(int i=1;i<n;i++)
30     {
31         minn=maxn;
32         for(int j=1;j<=n;j++)
33             if(!vis[j]&&minn>d[j])
34             {
35                 minn=d[j];
36                 k=j;
37             }
38         vis[k]=1;ans+=minn;
39         for(int j=1;j<=n;j++)
40         {
41             cnt=count(k,j);
42             if(!vis[j]&&d[j]>cnt)
43             d[j]=cnt;
44         }
45             
46     }
47     
48     printf("%.2lf",ans);
49     return 0;
50 }
稀里哗啦改了一通~~~AC

恶心~~~

posted @ 2017-04-08 16:54  Aptal丶  阅读(185)  评论(0)  编辑  收藏  举报