P3366 最小生成树【模板】 洛谷

https://www.luogu.org/problem/show?pid=3366

题目描述

如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出orz

输入输出格式

输入格式：

 

第一行包含两个整数N、M，表示该图共有N个结点和M条无向边。（N<=5000，M<=200000）

接下来M行每行包含三个整数Xi、Yi、Zi，表示有一条长度为Zi的无向边连接结点Xi、Yi

 

输出格式：

 

输出包含一个数，即最小生成树的各边的长度之和；如果该图不连通则输出orz

 

输入输出样例

输入样例#1：

4 5
1 2 2
1 3 2
1 4 3
2 3 4
3 4 3

输出样例#1：

7

说明

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=20

对于40%的数据：N<=50，M<=2500

对于70%的数据：N<=500，M<=10000

对于100%的数据：N<=5000，M<=200000

样例解释：

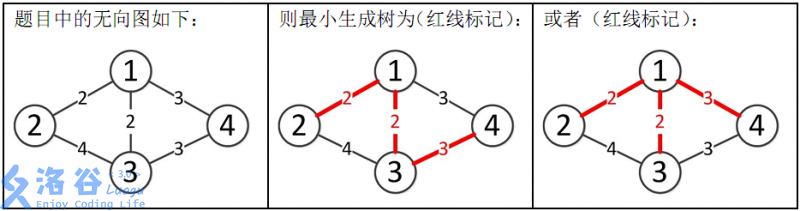
所以最小生成树的总边权为2+2+3=7

 

#include <algorithm>
#include <iostream>
#define maxn 100000007

using namespace std;

int m,n,ans,num[200005],fa[200005];
struct node
{
    int x,y,z;
}w[200005];

bool cmp(node a,node b)
{
    return a.z<b.z;
}

int find(int x)
{
    if(x!=fa[x])
        return fa[x]=find(fa[x]);
    return x;
}

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)    fa[i]=i;
    for(int i=1;i<=m;i++)
        cin>>w[i].x>>w[i].y>>w[i].z;
    sort(w+1,w+m+1,cmp);
    int tot=0;
    for(int i=1;i<=m;i++)
    {
        int xx=find(w[i].x),yy=find(w[i].y);
        if(xx!=yy)
        {
            fa[xx]=yy;
            tot++;
            ans+=w[i].z;
        }
        if(tot==n-1)
        {
            cout<<ans;
            return 0;
        }
    }
    if(tot!=n-1)
        cout<<"orz";
    return 0;
}