【模板】K-D Tree
一、\(kd-tree\)是用来干什么的
\(kd-tree\):KevinDurant-tree,不,不是这个,再来一次
\(kd-tree\):\(k-dimensional\) 树的简称
英语好的同学就会知道,\(dimensional\)是维度的意思,所以,\(kd-tree\)的字面意思就是:\(k\)维树
在这里,大家应该就知道\(kd-tree\)是用来干嘛的了
没错,是用来维护多维数据和查询多维数据的
在这一点上,多维数据的问题肯定困扰了很多学生,\(kd-tree\)就是专门用来解决这类问题的
但是蒟蒻发现基本主流考法都是考\(2\)维的,所以本文只讲\(2\)维的做法(啪,其实是自己不会多维的)
二、\(kd-tree\)是什么
\(kd-tree\)是一个\(BST\)(二叉搜索树)的变种
\(BST\)是什么?
\(BST\)的左子树的节点的关键字一定小于当前节点的关键字,右子树的节点的关键字一定大于当前节点的关键字
\(BST\)其实是对一个一维的东西进行划分
那么\(kd-tree\)就是对一个\(k\)维的东西进行划分
那么,大家都知道,\(kd-tree\)有\(k\)个关键字(即维度)。
现在我们需要考虑的是,在每一层应该按哪一个关键字来划分?
有一种策略是,计算出每一种维度的方差,挑选出方差最大那一个,这说明在这个维度上每个点分散的最开,所以可以划分得更*衡一点
但是在\(2\)维的情况下,我们一般将\(1,2\)维轮流使用
关于确定好每一层按哪个关键字后,我们就把点按照关键字排序,并取当前数列中的中间那一个,再对它的下一层进行遍历
不懂的我们先按\(2d-tree\)的情况来看看
我们可以看到这个图(手画的不要太难看)
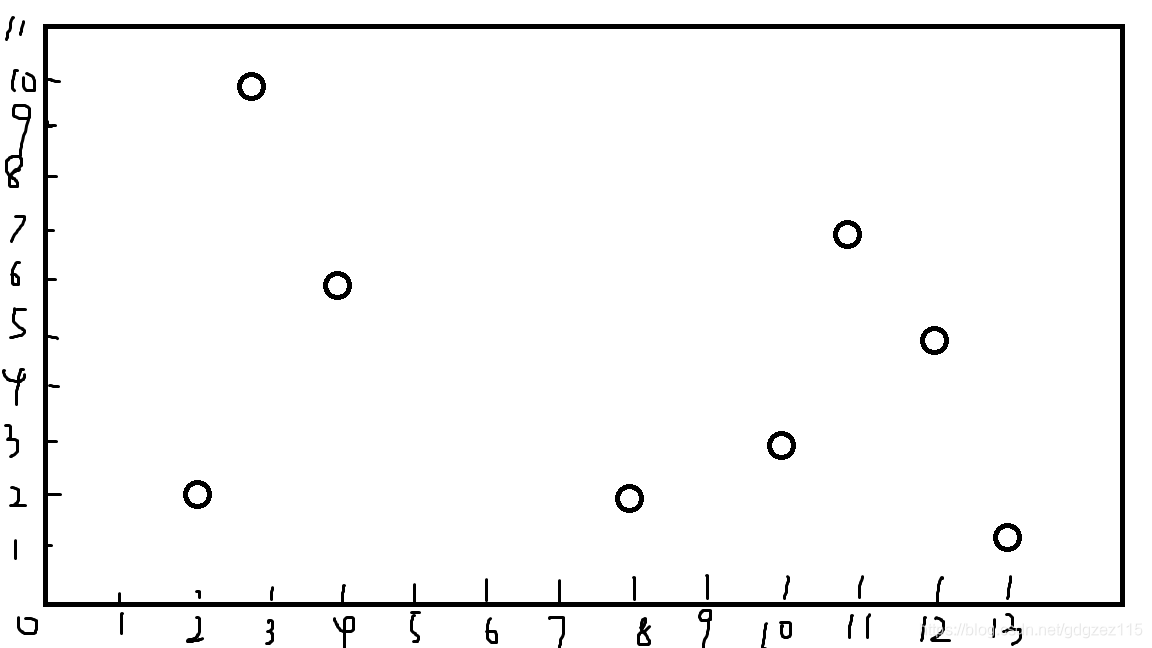
我们考虑首先按\(x\)来划分,取到最中间一个\((8,2)\)
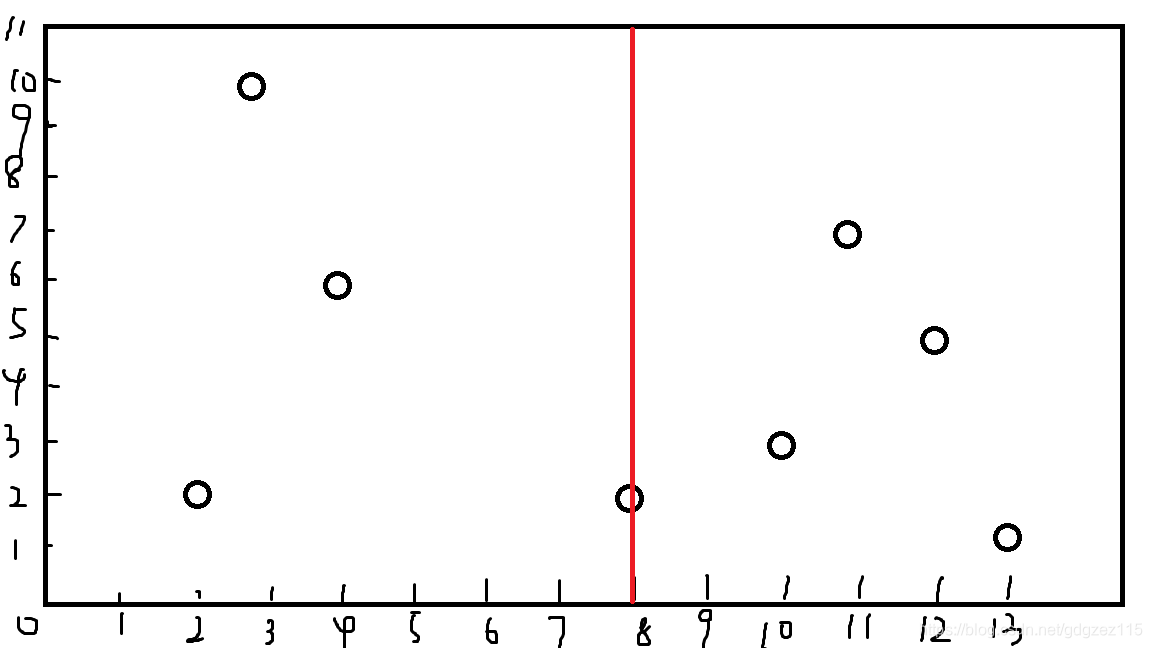
再按照\(y\)来,取到\((4,6)\)和\((10,3)\)
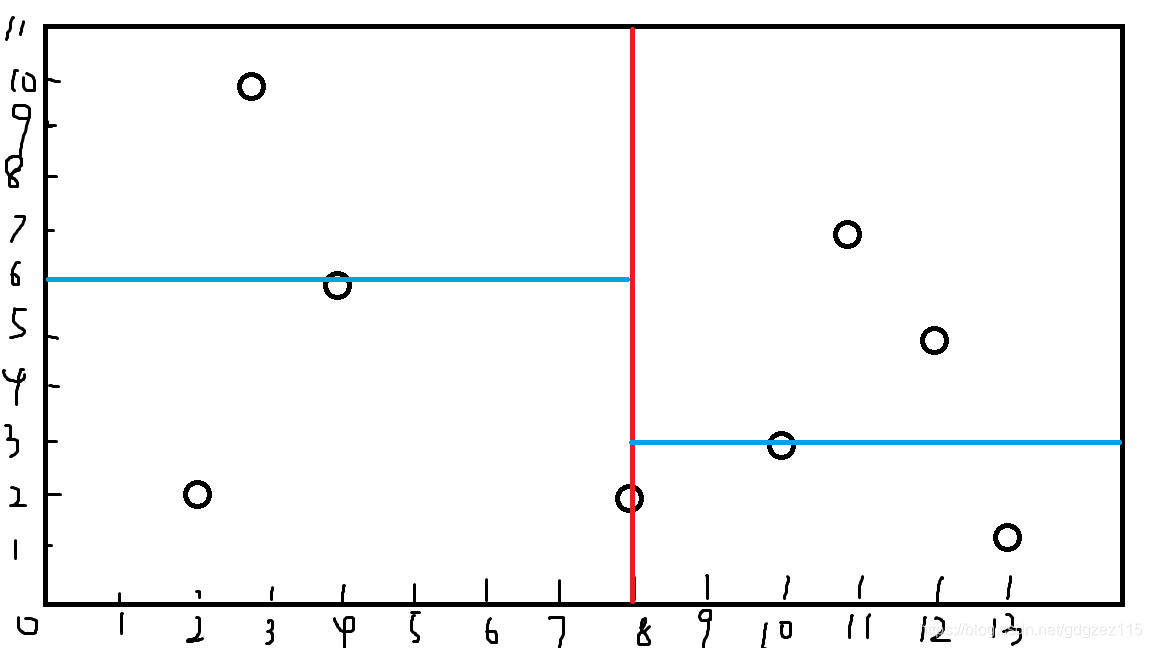
再按照\(x\)来
此时只需要划分右边的区间,取到\((11,7)\)

这样,一棵\(2d-tree\)就建好啦,建出来应该是这样的:
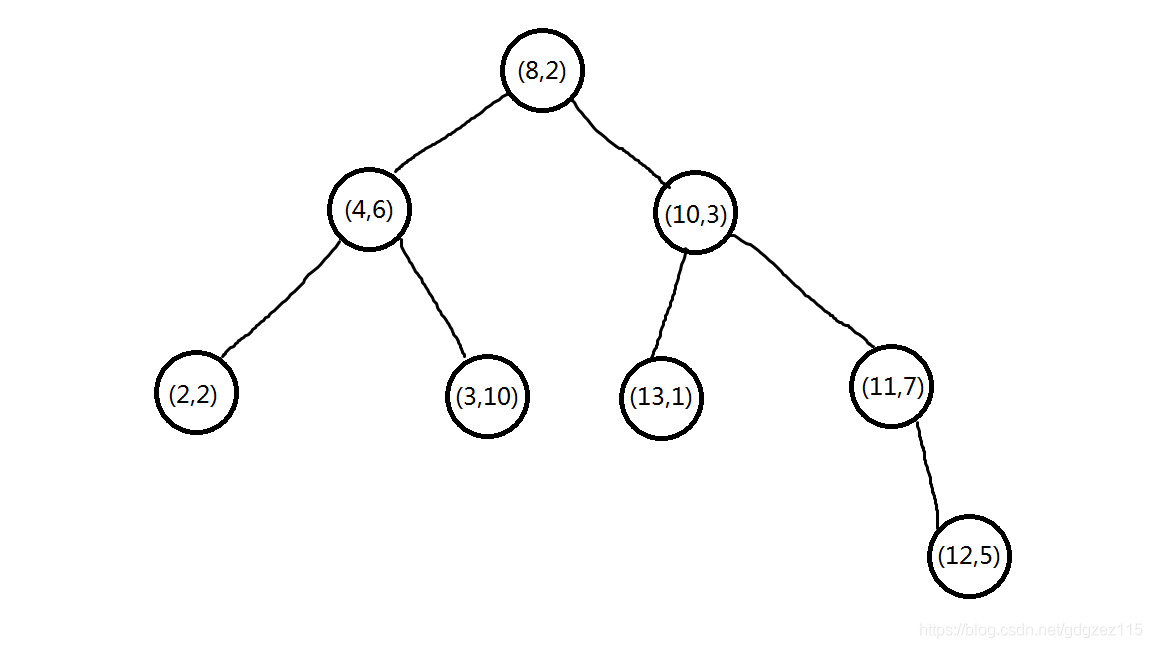
我们可以发现,这样建出来的\(kd-tree\)因为每次取中间数,所以建出来的树的叶子节点的深度都十分接*,可以*乎*衡,但是,并不是所有情况都可以保证*衡,所以,我们采用如替罪羊树一样的方法将不*衡的子树拍扁重建,这样使得树的高度在\(nlog_{n}\sim n\sqrt{n}\)之间(但是它十分不稳定...)
\(kd-tree\)的建树和原理都已经讲解完毕,大概就是这样一种*衡+替罪羊树的思想
三、例题
1.P4148 简单题
Description
内存限制为20MB
你有一个\(N×N\)的棋盘,每个格子内有一个整数,初始时的时候全部为\(0\),现在需要维护两种操作:
命令 参数限制 内容
\(1\) \(x\) \(y\) \(A\)
\(1≤x,y≤N\),\(A\)是正整数 将格子\(x,y\)里的数字加上\(A\)
\(2\) \(x_{1}\) \(y_{1}\) \(x_{2}\) \(y_{2}\)
\(1≤x_{1}≤x_{2}≤N,1≤y_{1}≤y_{2}≤N\) 输出\(x_{1}\) \(y_{1}\) \(x_{2}\) \(y_{2}\)这个矩形内的数字和
3 无 终止程序
\(Input\)
输入文件第一行一个正整数\(N\)。
接下来每行一个操作。每条命令除第一个数字之外,
均要异或上一次输出的答案\(lastans\),初始时\(lastans=0\)。
\(Output\)
对于每个\(2\)操作,输出一个对应的答案。
\(Sample Input\)
4
1 2 3 3
2 1 1 3 3
1 1 1 1
2 1 1 0 7
3
\(Sample Output\)
3
5
\(HINT\)
\(1≤N≤500000\),操作数不超过\(200000\)个,内存限制\(20M\),保证答案在\(int\)范围内并且解码之后数据仍合法。
Source
练习题 树8-8-KD-tree
思路
一道\(kd-tree\)模板题(要不然我为什么要放在第一题 )
我们考虑对于每一个操作\(2\),我们都将这个节点的\(x,y,val\)打包成一个\(struct\)插入\(kd-tree\)的每一个节点中,并维护五个值:\(maxx,maxy,minx,miny,sum\),前四个分别代表以这个节点为根节点的子树中的每个节点的\(x,y\)的最大值和最小值,\(sum\)代表以这个节点为根的子树中的权值和
考虑对于操作\(3\)
我们从根节点\(k\)开始向下遍历:
- 如果以这个子树为根的子树完全不在询问矩阵内,\(return\) \(0\)
- 如果\(\sim\)完全在询问矩阵内,\(return\) \(t[k].sum\)
- 如果以上两种情况都不是,说明有一部分在矩阵中,那么我们先判断当前节点\(k\)是否在矩阵中,如果是加上\(k\)自己的权值,再遍历左右子树,将答案求和
细节见代码
#include<bits/stdc++.h>
using namespace std;
const int N=200005;
const double alpha=0.725;
int n,rt,nodetot=0,topp=0,cnt=0;
struct point
{
int x[2],val;
}p[N];
struct tree
{
int lc,rc,siz,sum;
int maxn[2],minn[2];//maxn[0]表示maxx,minn[1]表示miny,以此类推
point pt;
}t[N];
int WD;
int rub[N];
bool cmp(point a,point b)
{
return a.x[WD]<b.x[WD];
}
int newnode()
{
if(topp)return rub[topp--];
return ++nodetot;
}
void update(int k)
{
t[k].siz=t[t[k].lc].siz+t[t[k].rc].siz+1;
t[k].sum=t[t[k].lc].sum+t[t[k].rc].sum+t[k].pt.val;
for(int i=0;i<=1;i++)
{
t[k].maxn[i]=t[k].minn[i]=t[k].pt.x[i];
if(t[k].lc)
{
t[k].maxn[i]=max(t[k].maxn[i],t[t[k].lc].maxn[i]);
t[k].minn[i]=min(t[k].minn[i],t[t[k].lc].minn[i]);
}
if(t[k].rc)
{
t[k].maxn[i]=max(t[k].maxn[i],t[t[k].rc].maxn[i]);
t[k].minn[i]=min(t[k].minn[i],t[t[k].rc].minn[i]);
}
}
}
bool bad(int k)//如替罪羊树一样判断是否*衡
{
return (t[k].siz*alpha<t[t[k].lc].siz||t[k].siz*alpha<t[t[k].rc].siz);
}
void work(int k)
{
if(t[k].lc)work(t[k].lc);
p[++cnt]=t[k].pt;
rub[++topp]=k;//将不用的节点编号存进rub中,节省空间
if(t[k].rc)work(t[k].rc);
}
int build(int l,int r,int wd)
{
if(l>r)return 0;
int mid=(l+r)>>1,k=newnode();
WD=wd;//每次按照当前维度排序
nth_element(p+l,p+mid,p+r+1,cmp);
//这是一个神奇的STL,会使得序列a中[l,r]中的第mid小的元素在第mid位上,但是其他元素并不有序!!!
//这个STL的时间复杂度为O(n),这也是我们不使用sort的原因,并且可以去到中位数
t[k].pt=p[mid];
t[k].lc=build(l,mid-1,wd^1);
t[k].rc=build(mid+1,r,wd^1);
update(k);
return k;
}
void rebuild(int &k)
{
cnt=0;
work(k);//拍扁
k=build(1,cnt,0);//重建
}
void ins(int &k,point tmp,int wd)
{
if(!k)//新建节点
{
k=newnode();
t[k].lc=t[k].rc=0;
t[k].pt=tmp;
update(k);
return ;
}
if(tmp.x[wd]<=t[k].pt.x[wd])ins(t[k].lc,tmp,wd^1);
else ins(t[k].rc,tmp,wd^1);
//判断应该插入进左子树还是右子树中
update(k);
if(bad(k))rebuild(k);//如果不*衡,拍扁重建
}
bool out(int nx1,int nx2,int ny1,int ny2,int x1,int y1,int x2,int y2)
{
if(x1>nx2||x2<nx1||y1>ny2||y2<ny1)return 1;
return 0;
}
bool in(int nx1,int nx2,int ny1,int ny2,int x1,int y1,int x2,int y2)
{
if(nx1>=x1&&nx2<=x2&&ny1>=y1&&ny2<=y2)return 1;
return 0;
}
int query(int k,int x1,int y1,int x2,int y2)
{
if(!k)return 0;
if(out(t[k].minn[0],t[k].maxn[0],t[k].minn[1],t[k].maxn[1],x1,y1,x2,y2))return 0;
//完全在矩阵外
if(in(t[k].minn[0],t[k].maxn[0],t[k].minn[1],t[k].maxn[1],x1,y1,x2,y2))return t[k].sum;
//完全在矩阵内
int res=0;
if(in(t[k].pt.x[0],t[k].pt.x[0],t[k].pt.x[1],t[k].pt.x[1],x1,y1,x2,y2))res+=t[k].pt.val;
//当前节点在矩阵内
return query(t[k].lc,x1,y1,x2,y2)+query(t[k].rc,x1,y1,x2,y2)+res;
}
inline int read()
{
int x=0,f=1;
char ch=getchar();
while(!isdigit(ch))
{
if(ch=='-')f=-1;
ch=getchar();
}
while(isdigit(ch))
{
x=(x<<3)+(x<<1)+(ch^48);
ch=getchar();
}
return x*f;
}
int main()
{
n=read();
int op,lastans=0,x,y,a,x1,y1;
while(1)
{
op=read();
if(op==3)return 0;
if(op==1)
{
x=read(),y=read(),a=read();
x^=lastans,y^=lastans,a^=lastans;
ins(rt,(point){x,y,a},0);
}
if(op==2)
{
x=read(),y=read(),x1=read(),y1=read();
x^=lastans,y^=lastans,x1^=lastans,y1^=lastans;
printf("%d\n",lastans=query(rt,x,y,x1,y1));
}
}
return 0;
}
/*
4
1 2 3 3
2 1 1 3 3
1 1 1 1
2 1 1 0 7
3
*/
2.P4357 [CQOI2016]K远点对
\(Description\)
已知*面内 \(N\) 个点的坐标,求欧氏距离下的第 \(K\) 远点对。
\(Input\)
输入文件第一行为用空格隔开的两个整数 \(N, K\)。接下来 \(N\) 行,每行两个整数 \(X,Y\),表示一个点
的坐标。\(1 < = N < = 100000\), \(1 < = K < = 100\), \(K < = N*(N−1)/2\) , \(0 < = X, Y < 2^{31}\)。
\(Output\)
输出文件第一行为一个整数,表示第 K 远点对的距离的*方(一定是个整数)。
\(Sample Input\)
10 5
0 0
0 1
1 0
1 1
2 0
2 1
1 2
0 2
3 0
3 1
\(Sample Output\)
9
思路
关于第\(k\)大怎么求,我们考虑使用小根堆。我们首先插入\(2\times k\)个\(0\)(插入\(2\times k\)个元素是因为每个距离会被算两次),存后\(k\)大的距离。我们每次从一个节点进去,然后在建好的\(kd-tree\)上遍历,将它对于每个节点的距离计算出来(这里使用两点距离公式计算),每次查询到当前距离如果大于堆顶,就把堆顶弹出,再把当前距离压进堆中。这样就可以保证堆中一直都是\(2\times k\)个元素,所以当全部节点都计算完后,这时的堆顶就是第\(K\)远大的距离
如果真的按照以上方法每个节点计算出与其他节点的所有距离的话,显而易见会被卡(这不废话吗 )
所以我们要剪枝
我们考虑每次都计算出这个节点对于当前遍历到的节点的左右儿子的节点中的最大距离,如果最大距离都不大于堆顶,就可以选择不进去遍历
那么最大距离怎么处理呢?
我们像上一题一样处理出每个节点的子树中的\(maxx,maxy,minx,miny\),然后用这四个元素处理出可能最大值
当然这个复杂度是\(O(玄学)\),谁都不知道这个剪枝能优化多少
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100010;
int n,k,nodetot=0;
priority_queue<ll,vector<ll>,greater<ll> >q;
struct point
{
int x[2];
}p[N];
struct tree
{
int lc,rc,siz;
int maxn[2],minn[2];
point pt;
}t[N];
int WD;
int rt;
bool cmp(point a,point b)
{
return a.x[WD]<b.x[WD];
}
int newnode()
{
return ++nodetot;
}
void update(int k)
{
for(int i=0;i<=1;i++)
{
t[k].maxn[i]=t[k].minn[i]=t[k].pt.x[i];
if(t[k].lc)
{
t[k].maxn[i]=max(t[k].maxn[i],t[t[k].lc].maxn[i]);
t[k].minn[i]=min(t[k].minn[i],t[t[k].lc].minn[i]);
}
if(t[k].rc)
{
t[k].maxn[i]=max(t[k].maxn[i],t[t[k].rc].maxn[i]);
t[k].minn[i]=min(t[k].minn[i],t[t[k].rc].minn[i]);
}
}
}
int build(int l,int r,int wd)
{
if(l>r)return 0;
int mid=(l+r)>>1,k=newnode();
WD=wd;
nth_element(p+l,p+mid,p+r+1,cmp);
// cout<<"p[mid].x[0]="<<p[mid].x[0]<<" "<<"p[mid].x[1]="<<p[mid].x[1]<<endl;
t[k].pt=p[mid];
t[k].lc=build(l,mid-1,wd^1);
t[k].rc=build(mid+1,r,wd^1);
update(k);
return k;
}
ll poww(int x){return (ll)x*x;}
ll getdis(int k,int x,int y)
//计算可能最大距离(并不是精确的!!!),所以这里并不会小,只可能大
//这里只是用来剪枝,所以正确性不会有影响,但是时间复杂度会减小
{
ll res=0ll;
res+=max(poww(t[k].maxn[0]-x),poww(t[k].minn[0]-x));
res+=max(poww(t[k].maxn[1]-y),poww(t[k].minn[1]-y));
return res;
}
void work(int k,int x,int y)
{
ll dis=0ll,dl=0ll,dr=0ll;
dis=poww(t[k].pt.x[0]-x)+poww(t[k].pt.x[1]-y);//计算当前节点到目标节点的距离
if(t[k].lc)dl=getdis(t[k].lc,x,y);
if(t[k].rc)dr=getdis(t[k].rc,x,y);
if(dis>q.top())q.pop(),q.push(dis);//如果大于,将堆顶弹出,将dis压入
//剪枝
if(dl>dr)//如果我们先遍历大的,那么就会先将大的压入堆中,那么小的就会少压入点
{
if(dl>q.top())work(t[k].lc,x,y);
if(dr>q.top())work(t[k].rc,x,y);
}
else
{
if(dr>q.top())work(t[k].rc,x,y);
if(dl>q.top())work(t[k].lc,x,y);
}
}
int main()
{
scanf("%d %d",&n,&k);
k<<=1;
for(int i=1;i<=k;i++)q.push(0);
for(int i=1;i<=n;i++)scanf("%d %d",&p[i].x[0],&p[i].x[1]);
rt=build(1,n,0);
for(int i=1;i<=n;i++)work(rt,p[i].x[0],p[i].x[1]);//对于每个节点进去遍历
printf("%lld",q.top());
return 0;
}
/*
8 5
2 2
4 6
8 2
3 10
10 3
11 7
12 5
13 1
*/
简化过后的题面:
\(Description\)
给出*面上\(N\)个点,现在需要从中选出一个点,使得 离该点最远的点到它的距离 与 离该点最*的点到它的距离 之差最小,输出最小的差值。
\(Input\)
第一行一个整数\(N\),表示点数
接下来\(N\)行,每行一个二元组描述一个点的坐标
\(Output\)
输出答案
\(Sample\) \(Input\)
4
0 0
1 0
0 1
1 1
\(Sample\) \(Output\)
1
思路
\(tips:\)这道题中的距离是曼哈顿距离,即 \(abs(x1-x2)+abs(y1-y2)\)
这道题可以发现,除了要求最大距离之外,还要求最小距离,所以我们依旧按照上题一样的处理最大距离,最小距离也差不多,但是在对最小距离进行剪枝的时候,需要有所思考
我们考虑,现在要求目标点对于一个矩形(将\(maxn[2],minn[2]\)看做一个矩形)的最小距离
这时,如果它在矩形内部,那么我们没有办法处理出最小距离(或者有但是蒟蒻不会),于是返回\(0\)
如果不在矩形内部,我们就考虑它到四个角或是四条边的距离
详见代码
int getmin(int k,int x,int y)
{
int res=0;
//以下情况都是不在矩形内的
if(x<t[k].minn[0])res+=t[k].minn[0]-x;
else if(x>t[k].maxn[0])res+=x-t[k].maxn[0];
if(y<t[k].minn[1])res+=t[k].minn[1]-y;
else if(y>t[k].maxn[1])res+=y-t[k].maxn[1];
return res;
}
于是其他代码也就差不多相同了(如果上面的你的看懂了,那么代码就不需要注释了)
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=100010;
const ll INF=0x7ffffffffff;
int n,topp=0,nodetot=0,WD,rt;
struct point
{
int x[2];
}p[N];
struct tree
{
int lc,rc,siz,maxn[2],minn[2];
point pt;
}t[N];
int rub[N];
int newnode()
{
if(topp)return rub[topp--];
return ++nodetot;
}
bool cmp(point a,point b)
{
return a.x[WD]<b.x[WD];
}
void update(int k)
{
t[k].siz=t[t[k].lc].siz+t[t[k].rc].siz+1;
for(int i=0;i<=1;i++)
{
t[k].maxn[i]=t[k].minn[i]=t[k].pt.x[i];
if(t[k].lc)
{
t[k].maxn[i]=max(t[k].maxn[i],t[t[k].lc].maxn[i]);
t[k].minn[i]=min(t[k].minn[i],t[t[k].lc].minn[i]);
}
if(t[k].rc)
{
t[k].maxn[i]=max(t[k].maxn[i],t[t[k].rc].maxn[i]);
t[k].minn[i]=min(t[k].minn[i],t[t[k].rc].minn[i]);
}
}
}
int build(int l,int r,int wd)
{
if(l>r)return 0;
int mid=(l+r)>>1,k=newnode();
WD=wd;
nth_element(p+l,p+mid,p+r+1,cmp);
t[k].pt=p[mid];
t[k].lc=build(l,mid-1,wd^1);
t[k].rc=build(mid+1,r,wd^1);
update(k);
return k;
}
ll maxd,mind;
ll getmax(int k,int x,int y)
{
ll res=0;
res+=max(abs(t[k].maxn[0]-x),abs(t[k].minn[0]-x));
res+=max(abs(t[k].maxn[1]-y),abs(t[k].minn[1]-y));
return res;
}
ll getmin(int k,int x,int y)
{
ll res=0ll;
if(x<t[k].minn[0])res+=t[k].minn[0]-x;
else if(x>t[k].maxn[0])res+=x-t[k].maxn[0];
if(y<t[k].minn[1])res+=t[k].minn[1]-y;
else if(y>t[k].maxn[1])res+=y-t[k].maxn[1];
return res;
}
ll getdis(int k,int x,int y)//曼哈顿距离
{
return abs(t[k].pt.x[0]-x)+abs(t[k].pt.x[1]-y);
}
void query_max(int k,int x,int y)
{
if(!k)return ;
ll dis=0ll,dl=0ll,dr=0ll;
dis=getdis(k,x,y);
maxd=max(maxd,dis);
if(t[k].lc)dl=getmax(t[k].lc,x,y);
if(t[k].rc)dr=getmax(t[k].rc,x,y);
if(dl>dr)
{
if(dl>maxd)query_max(t[k].lc,x,y);
if(dr>maxd)query_max(t[k].rc,x,y);
}
else
{
if(dr>maxd)query_max(t[k].rc,x,y);
if(dl>maxd)query_max(t[k].lc,x,y);
}
}
void query_min(int k,int x,int y)
{
if(!k)return ;
ll dis,dl=INF,dr=INF;
dis=getdis(k,x,y);
if(dis)mind=min(mind,dis);
if(t[k].lc)dl=getmin(t[k].lc,x,y);
if(t[k].rc)dr=getmin(t[k].rc,x,y);
if(dl<dr)
{
if(dl<mind)query_min(t[k].lc,x,y);
if(dr<mind)query_min(t[k].rc,x,y);
}
else
{
if(dr<mind)query_min(t[k].rc,x,y);
if(dl<mind)query_min(t[k].lc,x,y);
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d %d",&p[i].x[0],&p[i].x[1]);
rt=build(1,n,0);
ll ans=INF;
for(int i=1;i<=n;i++)
{
maxd=-INF,mind=INF;
query_max(rt,p[i].x[0],p[i].x[1]);
query_min(rt,p[i].x[0],p[i].x[1]);
ans=min(ans,(maxd-mind));
}
printf("%d",ans);
return 0;
}
4.[CH弱省胡策R2]TATT
\(Description\)
四维空间真是美妙。 现在有\(n\)个四维空间中的点,请求出一条最长的路径,满足任意一维坐标都是单调不降的。 注意路径起点是任意选择的,并且路径与输入顺序无关(路径顺序不一定要满足在输入中是升序)。
路径的长度是经过的点的数量,任意点只能经过一次。
\(Input\)
第一行一个整数\(n\)。 接下来\(n\)行,每行四个整数\(a_{i},b_{i},c_{i},d_{i}\)。表示四维坐标
\(Ouput\)
一行一个整数,表示最长路径的长度
\(Sample\) \(Input\)
4
2 3 33 2333
2 3 33 2333
2 3 33 2333
2 3 33 2333
\(Sample\) \(Output\)
4
思路
啪,完全打脸上方
我终于会做不是二维偏序的多维偏序了啊啊(激动)
小声\(bb\):这不就是一个四维偏序板子题吗
好,现在我们看回正题
对于这个四维偏序,我们先将它的第一维进行排序,接下来就是三维偏序了
我们对于每一个点一个一个的插入到\(3d-tree\)中,我们对于每一个点存一个\(val\),表示插入这个点前的最大距离,于是每次初始化所有\(val=1\),然后在插入当前点\(k\)前\(query\)一遍当前所有点到它的最大距离,然后将\(t[k].val+=ans\),每次都将最后输出的答案与\(t[k].val\)取\(max\),就可以了
在\(query\)的时候,我们需要判断目标点对于当前矩形是否完全满足偏序,这里要分完全满足、部分满足和完全不满足三种情况处理
#include<bits/stdc++.h>
using namespace std;
const int N=500010;
const int INF=1e9+7;
const double alpha=0.725;
int n,topp=0,nodetot=0,rt,tot=0;
int rub[N];
int WD;
struct point
{
int x[4],val;
}p[N],o[N];
struct tree
{
int lc,rc,siz,mx,d;
int maxn[4],minn[4];
point pt;
}t[N];
bool cmp(point a,point b)
{
return a.x[WD]<b.x[WD];
}
int newnode()
{
if(topp)return rub[topp--];
return ++nodetot;
}
void update(int k)
{
t[k].mx=max(t[k].pt.val,max(t[t[k].lc].mx,t[t[k].rc].mx));
t[k].siz=t[t[k].lc].siz+t[t[k].rc].siz+1;
for(int i=1;i<=3;i++)
{
t[k].maxn[i]=t[k].minn[i]=t[k].pt.x[i];
if(t[k].lc)
{
t[k].maxn[i]=max(t[k].maxn[i],t[t[k].lc].maxn[i]);
t[k].minn[i]=min(t[k].minn[i],t[t[k].lc].minn[i]);
}
if(t[k].rc)
{
t[k].maxn[i]=max(t[k].maxn[i],t[t[k].rc].maxn[i]);
t[k].minn[i]=min(t[k].minn[i],t[t[k].rc].minn[i]);
}
}
}
int build(int l,int r,int wd)
{
if(l>r)return 0;
int mid=(l+r)>>1,k=newnode();
WD=wd;
nth_element(o+l,o+mid,o+r+1,cmp);
t[k].pt=o[mid];
t[k].d=wd;
t[k].lc=build(l,mid-1,(wd+1)%3+1);
t[k].rc=build(mid+1,r,(wd+1)%3+1);
update(k);
return k;
}
bool cmp1(point a,point b)//先排序第一维
{
for(int i=0;i<=3;i++)
{
if(a.x[i]<b.x[i])return 1;
if(a.x[i]>b.x[i])return 0;
}
return 0;
}
int ans=0;
int check(point a,point b)
{
for(int i=1;i<=3;i++)if(a.x[i]>b.x[i])return 0;
return 1;
}
int inandout(int a,point b)
{
if(!a)return 0;
int cnt=0;
for(int i=1;i<=3;i++)
if(t[a].maxn[i]<=b.x[i])cnt++;
if(cnt==3)return cnt;
cnt=1;
for(int i=1;i<=3;i++)
{
if(t[a].minn[i]>b.x[i])//只要有一个最小值大于目标点,就一定不满足
{
cnt=0;
break;
}
}
return cnt;
}
void query(int k,point tmp)
{
if(check(t[k].pt,tmp))ans=max(ans,t[k].pt.val);//当前处理到的点是否满足偏序
int dl=inandout(t[k].lc,tmp),dr=inandout(t[k].rc,tmp);
if(dl==3)ans=max(ans,t[t[k].lc].mx);//左子树的矩形完全满足偏序
else if(dl&&ans<t[t[k].lc].mx)query(t[k].lc,tmp);//部分满足
if(dr==3)ans=max(ans,t[t[k].rc].mx);
else if(dr&&ans<t[t[k].rc].mx)query(t[k].rc,tmp);
}
bool bad(int k)
{
if(t[k].siz*alpha<t[t[k].lc].siz||t[k].siz*alpha<t[t[k].rc].siz)return 1;
return 0;
}
void work(int k)
{
if(t[k].lc)work(t[k].lc);
o[++tot]=t[k].pt;
rub[++topp]=k;
if(t[k].rc)work(t[k].rc);
}
void rebuild(int &k)
{
tot=0;
work(k);
k=build(1,tot,t[k].d);//从当前的维度开始建,优化时间
}
void ins(int &k,point tmp,int wd)
{
if(!k)
{
k=newnode();
t[k].lc=t[k].rc=0;
t[k].d=wd;//这里特殊记录一下维度
t[k].pt=tmp;
update(k);
return ;
}
if(t[k].pt.x[wd]<=tmp.x[wd])ins(t[k].lc,tmp,(wd+1)%3+1);
else ins(t[k].rc,tmp,(wd+1)%3+1);
update(k);
if(bad(k))rebuild(k);
}
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d %d %d %d",&p[i].x[0],&p[i].x[1],&p[i].x[2],&p[i].x[3]),p[i].val=1;
sort(p+1,p+n+1,cmp1);
int output=0;
for(int i=1;i<=n;i++)
{
ans=0;
query(rt,p[i]);
p[i].val+=ans;
output=max(output,p[i].val);
ins(rt,p[i],1);
}
printf("%d\n",output);
return 0;
}
/*
4
2 3 33 2333
2 3 33 2333
2 3 33 2333
2 3 33 2333
*/
四、总结
对于一系列的多维数据和询问的题目,我们可以考虑使用整体二分或者\(CDQ\)处理,但是很不巧的是\(K-D\) \(Tree\)这些都可以处理。我个人的理解来看,\(K-D\) \(Tree\)是一个经过优化的暴力,靠维度的划分来完善复杂度和正确性,所以\(K-D\) \(Tree\)本身并不难理解,难的是它的应用和扩展

