数学学习笔记（持续更新中）

数学学习笔记

前言

要开始学数学（数论）了，于是特开一个专题来记录一下相关知识和有关问题。

0.矩阵与快速幂

这里我认为与数学关系不是很大，于是一笔带过吧。

矩阵，是 $n\times m$ 个数 $a_{i,j}$ 组成的数表，称为 $m$ 行 $n$ 列的矩阵。

记作： $A=\begin{bmatrix}a_{1,1} & a_{2,1}&\cdots&a_{1,m}\\a_{2,1}&a_{2,2}&\cdots& a_{2,n}\\ \vdots&\vdots&\ddots&\vdots\\a_{n,1} & a_{n,2}&\cdots&a_{n,m} \end{bmatrix}$.

特别定义：单位矩阵 $I$ ，其中 $a_{i,i} = 1$，其余为 $0$ 。
其性质：任意次方等于自己，与任意矩阵相乘等于另一矩阵。

矩阵乘法

令 $C=A\times B$ 。

若 $A$ 是 $n\times r$ 的矩阵， $B$ 是 $r\times m$ 的矩阵，那么 $C$ 是 $n\times m$ 的矩阵。
定义： $C_{i,j} = \sum\limits_{k=1}^r A_{i,k}\times B_{k,j}$

矩阵乘法满足交换律，不满足结合律。

另外，矩阵内可以内套矩阵。形如 $P=\begin{bmatrix}A&B\\C&D\end{bmatrix}$ ，其中 $A$ ，$B$ ， $C$ ， $D$ 为矩阵。它仍然满足矩阵乘法的规律。

矩阵快速幂

顾名思义，矩阵快速幂，就是矩阵的多次乘方。过程用快速幂优化。

模板：【【模板】矩阵快速幂】。

应用

可以用它来解决形如 $F_n=p\times F_{n-1}+q\times F_{n-2}+\cdots$ 的递推式。

甚至，形如 $f(i,j) = \sum f(i,k)\times f(k,j)$ 的动态规划也可用其解决。

例题

【P1349 广义斐波那契数列】

【P3758 可乐】

1.质数与约数

结论

对于一个足够大的整数，不超过 $N$ 的质数大约有 $\dfrac N{\ln N}$ 个，即每 $\ln N$ 个数中有一个质数。
算数基本定理：正整数 $N$ 可以唯一分解成有限个质数的乘积，即 $N=p_1^{c_1}p_2^{c_2}\cdots p_m^{c_m}$ ，其中 $p$ 都是质数， $c$ 都是正整数，且满足 $p_1 <p_2<\cdots<p_m$ .
$N$ 的正约数个数为 $\prod\limits_{i=1}^m (c_i+1)$ .
$N$ 的所有正约数和为

\[\prod \limits_{i=1}^m\begin{pmatrix}\sum\limits_{j=0}^{c_i} (p_i)^j\end{pmatrix} \]

对于上一个式子，其中有$\sum\limits_{j=0}^{c_i} (p_i)^j$ .

它是一个等比数列的求和。

对于等比数列的求和，设首项为 $a_1$ ，公比为 $q$ ，其公式为： $S_n = \dfrac{a_1(q^n-1)}{q-1}$ .

证明：

\[\begin{aligned}S_n=& \ a_1+& a_1\times q& + a_1\times q^2+\cdots+a_1\times q^{n-1} & \\S_n\times q= & & a_1\times q& + a_1\times q^2+\cdots+a_1\times q^{n-1}& + a_1\times q^n\end{aligned} \]

上下相减，移项，得到公式。

线性筛

先放代码

bool vis[M];
int pri[N],cnt;
void Prime(){
	for(int i = 2 ; i <= n ; i ++){
		if(!vis[i]) pri[++cnt] = i;
		for(int j = 1 ; j <= cnt && i * pri[j] <= n ; j ++){
			vis[i*pri[j]] = 1;
			if(!(i % pri[j])) break;
		}
	}
}

下面来详细解释：

vis[i] 表示 $i$ 这个数是否被筛去过（其实也可以用它来记录某个数的最小质因子）。

其本质，是用每个数的最小质因子（即为 pri[j] ）来筛去这个数。

为什么判断break在后面？

考虑用 $2$ 筛去 $4$ .

正确性与复杂度的证明

以下内容参照欧拉筛筛素数 - 学委的博客

设一合数 $C$（要筛掉）的最小质因数是 $p1$，令 $B = \dfrac C {p_1}$（$C = B \times p_1$），则 $B$ 的最小质因数不小于 $p_1$ 否则 $C$ 也有这个更小因子）。那么当外层枚举到 $i = B$ 时，我们将会从小到大枚举各个质数；因为 $i = B$ 的最小质因数不小于 $p_1$，所以 $i$ 在质数枚举至 $p_1$ 之前一定不会 break，这回，$C$ 一定会被 $B \times p_i$ 删去。

注意这个算法一直使用“某数×质数”去筛合数，又已经证明一个合数一定会被它的最小质因数 $p_1$ 筛掉，所以我们唯一要担心的就是同一个合数是否会被“另外某数 × $p_1$ 以外的质数”再筛一次导致浪费时间。设要筛的合数是 $C$，设这么一个作孽的质数为 $p_x$，再令 $A = \dfrac C {p_x}$，则 $A$ 中一定有 $p_1$ 这个因子。当外层枚举到 $i = A$，它想要再筛一次 $C$，却在枚举 $Prime[j] = p_1$ 时，因为 $i \mod Prime[j] == 0$ 就退出了。因而 $C$ 除了 $p_1$ 以外的质因数都不能筛它。

例题

质数距离

【UVA10140 Prime Distance】

给定两个整数 $L,R$ ，求 $[L,R]$ 中相邻两个质数的差最大以及最小是多少，输出这两个质数。
$1\leq L\leq R\leq2^{31}-1,0\leq R-L\leq 10^7$

解析

$L,R$ 很大，我们不能筛出所有的质数。

但是，可以筛出 $\sqrt R$ 以内的质数，用这些质数来筛 $[L,R]$ 的质数，并存储在 $p[i-l]$ 中。

int n,m;
int pri[N];bool vis[N];
void Prime(){
	for(int i = 2 ; i <= 1e6 ; i ++){
		if(!vis[i]) pri[++m] = i;
		for(int j = 1 ; j <= m && i * pri[j] <= 1e6 ; j ++){
			vis[i*pri[j]] = 1;
			if(!(i % pri[j])) break;
		}
	} 
}	
int p[N];
signed main(){
	ll l,r;
	Prime();
	while(scanf("%lld %lld",&l,&r) != EOF){
		memset(vis,0,sizeof(vis)); n = 0; 
		if(l == 1)vis[0] = 1;
		for(int j = 1 ; j <= m ; j ++)
			for(int i = l/pri[j] ; 1ll * i * pri[j] <= r ; i ++)
				if(i > 1)
					vis[i*pri[j]-l] = 1;
		for(int i = l ; i <= r ; i ++)
			if(!vis[i-l]) p[++n] = i;
		if(n < 2){puts("There are no adjacent primes.");continue;}
		int mx1 = p[1], mx2 = p[2],
			mn1 = p[1], mn2 = p[2];
		for(int i = 3 ; i <= n ; i ++){
			if(p[i]-p[i-1] > mx2-mx1) mx2 = p[i], mx1 = p[i-1];
			if(p[i]-p[i-1] < mn2-mn1) mn2 = p[i], mn1 = p[i-1];
		}
		printf("%d,%d are closest, %d,%d are most distant.\n",mn1,mn2,mx1,mx2);
	}
	return 0;
}

不定方程

【不定方程】

求不定方程： $\dfrac 1x+\dfrac1y=\dfrac1{n!}$的正整数解 $(x,y)$ 的数目。

$n\leq10^6$.

解析

先把式子改写一下，变成 $y=\dfrac{x\cdot n!}{x-n!}$ 。

令 $t = x-n!$ ，则原式变为 $y=n!+\dfrac {(n!)^2}t$ .

则问题转化为：求出 $(n!)^2$ 的约数总数。

根据上述的结论，可知对于正整数 $N$ ，其约数共有 $\prod(c_i+1)$。

那么，对于正整数 $N^2$ ，其约数共有 $\prod(2\times c_i+1)$。

对于求 $n!$ 的约数，我们有如下做法：

for(int i = 1 ; i <= m ; i ++)
		for(ll j = pri[i] ; j <= n ; j *= pri[i])
			(c[i] += n/j) %= mod;

下面详细解释一下：

比如我们考虑 $n=9$ ，先提取出其 $2$ 的倍数为 $9!=\cdots\times2\times4\times6\times8\times\cdots$.

使用质因子 $2$ 来筛：

\[2=2\times\cdots\\4=2\times2\times\cdots\\6=2\times\cdots\\8=2\times2\times2\times\cdots\\\cdots \]

形象化地，如下图：

图源：conprour

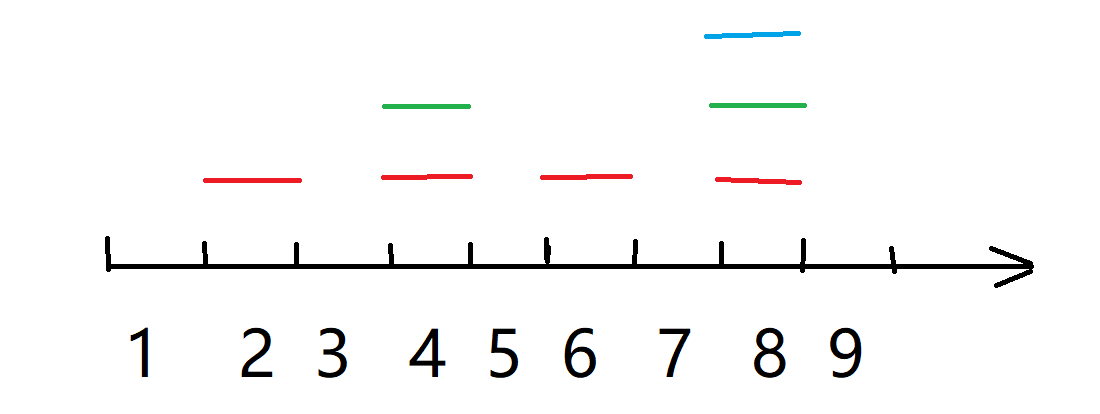
我们求和，相当于每次求一个竖列的和并相加。

用如上代码，我们可以便捷地： $+$ 红（$4$），$+$绿（$2$）$\cdots$

于是它成立。

ll n,k,ans;
void solve(){
	ll l,r;
	for(l = 1 ; l <= n ; l = r + 1){
		if(k/l) r = min(n,k/(k/l));
		else r = n;
		ans -= k/l * (l+r) * (r-l+1) >> 1;
	} 
}
signed main(){
	n = read(), k = read();
	ans = n * k;
	solve();
	printf("%lld",ans);
	return 0;
}

余数之和

给定 $n,k$ ，求

\[G(n,k)=\sum_{i=1}^n k\bmod i \]

$1\leq n,k\leq10^9$ 。

题解

已知： $k\bmod i = k-\left\lfloor\dfrac ki\right\rfloor$ 。

那么，对于原式，就是求

\[\begin{aligned} G(n,k)&=\sum _{i=1}^n (k - \left\lfloor \dfrac ki\right\rfloor)\\ &=n\times k - \sum_{i=1}^n\left\lfloor\dfrac ki\right\rfloor \end{aligned} \]

其中， $\sum \lfloor\frac ki\rfloor$ 如果暴力求，是 $O(n)$ 的。

但是，用一些方法，我们可以让它低至 $O(\sqrt n)$ 。

整除分块

整除分块，可以解决如同：求 $\sum \lfloor\frac ki\rfloor$ 的问题。复杂度是 $O(\sqrt n)$ 。

我们可以发现，对于 $\lfloor\frac ki\rfloor$ 的式子，随着 $i$ 的增加，式子的值是类似阶梯块状单调不降的。

结论：对于 $\lfloor\frac ki\rfloor$ 取值相同的 $i$ ，设其取值相同时 $i\in[l,r]$ ，则对于确定的 $l$ ，则 $r = \left\lfloor\dfrac k{\left\lfloor\dfrac kl\right\rfloor}\right\rfloor$ 。

证明：

懒得证明了，反正它是对的 QWQ 。

对于本题来说，在一个块内，则是 $\left\lfloor\dfrac kl\right\rfloor\times \sum\limits_{i=l}^ri = \left\lfloor\dfrac kl \right\rfloor\times \dfrac{(l+r)\times (r-l+1)}2$ 。

ll n,k,ans;
void solve(){
	ll l,r;
	for(l = 1 ; l <= n ; l = r + 1){
		if(k/l) r = min(n,k/(k/l));
		else r = n;
		ans -= k/l * (l+r) * (r-l+1) >> 1;
	}
}
signed main(){
	n = read(), k = read();
	ans = n * k;
	solve();
	printf("%lld",ans);
	return 0;
}

哈希函数（质因数分解）

设 $x,y$ 的hash函数为：$h=x\times y+x+y$。对于给出一个 $h$ 值，问有多少对 $(x,y)$ 满足 $\max(x,y)\leq h$ ， $h,x,y$ 都为非负整数。

$h\leq 10^8,T\leq10^4$

题解

终于能不看题解做出数论的题了！

由于给定函数，可知 $h \ge \max(x,y)$ 恒成立。于是不需考虑这个条件。

移项，变成 $y = \dfrac{h-x}{x+1}$ 。

设 $t = x +1$ ，则原式变为： $y = \dfrac{h-t+1}t = \dfrac {h+1}t-1$ 。

则直接统计 $h+1$ 的因子个数即可。

用这道题也可以练一下质因数分解。

ll n;
bool vis[N];
int pri[N],pcnt;
void Prime(){
	for(int i = 2 ; i <= 1e4 ; i ++){
		if(!vis[i]) pri[++pcnt] = i;
		for(int j = 1 ; j <= pcnt && i * pri[j] <= 1e4 ; j ++){
			vis[i*pri[j]] = 1;
			if(!(i%pri[j])) break;
		}
	}
}
int cnt,c[N],p[N];
inline bool isprime(ll x){
	ll ed = sqrt(x);
	for(int i = 2 ; i <= ed ; i ++) if(!(x % i)) return 0;
	return 1;
}
void work(){
	ll x = n = read()+1;
	memset(c,0,sizeof(c));
	cnt = 0;
	for(int i = 1 ; i <= pcnt ; i ++){
		if(!(x % pri[i])) p[++cnt] = pri[i];
		while(!(x % pri[i])) c[cnt] ++ , x /= pri[i];
		if(x == 1) break;
	}
	ll ans = 1;
	if(x > 1e4 && isprime(x))p[++cnt] = x,c[cnt] = 1;
	for(int i = 1 ; i <= cnt ; i ++)
		ans *= (c[i]+1);
	printf("%lld\n",ans);
}
signed main(){
	Prime();
	int T = read();
	while(T--) work();
}

数字对

对于一个数字对 $(a,b)$ ，我们可以通过一次操作将其变为新数字对 $(a+b, b)$ 或 $(a, a+b)$ 。

给定一正整数 $n$ ，问最少需要多少次操作可将数字对 $(1, 1)$ 变为一个数字对，该数字对至少有一个数字为 $n$。

题解

又是自己想出来的！

发现逆过程和更相减损法相同，于是直接枚举 $(n,x)$ 的 $x$ ，进行更相减损法就可以。

注意：深搜需要进行最优性剪枝。

void solve(int a,int b,int dep){
	if(dep > ans) return;
	if(a == 1 && b == 1) {ans = min(ans,dep);return;}
	if(a == b) return;
	if(a < b) swap(a,b);
	solve(a-b,b,dep+1);
}
signed main(){
	n = read();
	if(n == 1){puts("0");return 0;}
	for(int i = 1 ; i < n ; i ++)
		solve(n,i,0);
	printf("%d",ans);
}

后续

看了一下题解的做法，题解还是更巧妙……

上述和我的相同，但是不同的部分在于，在辗转相减的过程中，可以直接改为辗转相除进行优化，时间效率显著提升（其实并没有？）

void solve(int a,int b,int dep){
	if(dep-1 > ans) return;
	if(!b){
		if(a == 1) ans = min(ans,dep-1);
		return;
	}
	solve(b,a%b,dep+a/b);
}
signed main(){
	n = read();
	if(n == 1){puts("0");return 0;}
	for(int i = 1 ; i < n ; i ++)
		solve(n,i,0);
	printf("%d",ans);
}

灯光控制

学校宿管有一套神奇的控制系统来控制寝室的灯的开关：

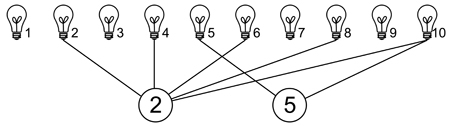
共有 $n$ 盏灯，标号为 $1$ 到 $n$ ，有 $m$ 个标有不同质数的开关，开关可以控制所有标号为其标号倍数的灯，按一次开关，所有其控制的灭着的灯都点亮，所有其控制的亮着的灯将熄灭。现在，宿管可以无限的按所有开关，所有灯初始状态为熄灭，请求出最多能点亮几盏灯。

$n\leq1000,m\leq\{n\texttt{以内的质数的总个数}\}$。

题解

没有想出……

对于 $i\leq \sqrt n$ ，所有的质数最多有 $11$ 个，这里爆搜就可以。
对于 $i\ge \sqrt n$ ，每个灯最多只会被唯一一个$\ge\sqrt n$ 的 $i$ 覆盖一次。这里在前一个条件完全做完后，依次枚举即可。

对于2.，可以使用贪心。如果答案变大就一定保留它。（原因还是只会被修改一次）。

注意：所有的统计答案应该在 1.、2.全部做完后进行，否则答案可能不会最优！

int n,m;0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000int pri[N];bool c[N],wrk[N]; int ans;void dfs(int cur,const int lim){	if(cur == lim+1){		memset(c,0,sizeof(c));		for(int i = 1 ; i <= lim ; i ++)			if(wrk[i])				for(int j = 1 ; j * pri[i] <= n ; j ++)					c[j * pri[i]] ^=  1;		int ret = 0;		for(int i = 1 ; i <= n ; i ++) ret += c[i];		for(int i = lim+1 ; i <= m ; i ++){			int delt = 0;			for(int j = 1 ; j * pri[i] <= n ; j ++)				delt += c[j*pri[i]] ? -1 : 1;			if(delt > 0){				ret += delt;				for(int j = 1 ; j * pri[i] <= n ; j ++)					c[j*pri[i]] ^= 1;			}		}		ans = max(ans,ret);		return;	}	wrk[cur] = 0;dfs(cur+1,lim);	wrk[cur] = 1;dfs(cur+1,lim);}void work(){	n = read(), m = read();	for(int i = 1 ; i <= m ; i ++) pri[i] = read();	sort(pri+1,pri+m+1);	int lim = upper_bound(pri+1,pri+m+1,sqrt(n))-pri-1;	ans = 0;	dfs(1,lim);	printf("%d\n",ans);}signed main(){	int T = read();	while(T--) work();}

最大公约数

有 $n$ 个数字 $a_1,a_2,\cdots，a_n$ ，求 $\max\gcd(a_i,a_j)(i\neq j)$。

$n\leq10000,1\le a_i\le 10^6$。

题解

自己做出来就是舒服！

开始有点想偏了，想到质因数分解去了……

这里，直接枚举 $\sqrt {a_i}$ 以下的 $a_i$ 的因数，并给其另一个因数打上标记。最后找到最大的标记数 $\ge2$ 的就是答案了。

signed main(){	n = read();	for(int i = 1 ; i <= n ; i ++) a[i] = read();	int mx = 0;	for(int i = 1 ; i <= n ; i ++){		int ed = sqrt(a[i]);		mx = max(mx,a[i]);		for(int j = 1 ; j <= ed ; j ++)			if(!(a[i] % j)) {				stk[j]++, stk[a[i]/j] ++;				if(j*j == a[i]) stk[j] --;			}	}	for(int i = mx ; i ; i --)		if(stk[i] > 1){			printf("%d",i);			return 0;		}}

总结

质数与约数算是数论的入门章节，其变化也不是很多。

主要知识就是算数基本定理、筛法求质数、除法分块。而常常配合其他算法使用。

从这里入门，大概有了数论的思路：

得到式子，用技巧简化计算。

2.同余问题

结论

一、基础概念

$a|b$ ，$a$ 能整除$b$ 。
$a\equiv b\pmod m$ ：$a$ 与 $b$ 在模 $m$ 意义下同余。
$\varphi(n)$ ：欧拉函数，表示 $[1,n]$ 中与 $n$ 互质的数的个数。

二、同余

$a\equiv b\pmod m\Leftrightarrow m|(a-b)\Leftrightarrow a=b+k\times m$

同余有如下性质：

自反性、对称性、传递性、同加/减/乘/幂性（没有同除性）。

另外：

$a\equiv x \pmod p,a\equiv x\pmod q$ ，其中 $p,q$ 互质，那么 $a\equiv x\pmod{(pq)}$ .
若 $\gcd(a,b) = 1$ ，则 $\forall i,j(i\not\equiv j\pmod p),a\times i\not\equiv a\times j\pmod p$ .
当 $\gcd(a,n) = 1$ 时，$\forall i(\gcd(i,j) = 1),\gcd(a\times i\bmod n,n0) = 1$ 0.

相关定理

费马小定理

若 $p$ 是质数，则对于任意整数 $a$ ，有$a^p\equiv a\pmod p$ .

推论：若 $p$ 是质数00000，且$p\nmid a$ 时， $a^{p-1}\pmod p$ .

欧拉函数

若 $n=p^k$ ，则 $\varphi(n) = p^k-p^{k-1}$ .
设互质的两个正整数 $n,m$ ，那么 $\varphi (nm)=\varphi(n)\times\varphi(m)$ .
设 $N = \prod\limits_{i=1}^n p_i^{k_i}$ ，则 $\varphi(N) = N \times\prod\limits_{i=1}^n(1-\dfrac 1{p_i})$ .
$\varphi(N)=\prod\limits_{i=1}^n \varphi(p_i^{p_i})$

欧拉定理

当 $\gcd(a,n)=1$ 时，有 $a^{\varphi(n)} \equiv 1\pmod n$ .

推论：若 $\gcd(a,n)=1$ ，则 $a^b\equiv a^{p\,\bmod\, \varphi(n)}\pmod n$ .

扩展欧拉定理：若 $b\ge\varphi(n)$ ，则 $a^b\equiv a^{b\,\bmod\,\varphi(n)+\varphi(n)}\pmod n$ .

根据欧拉定理，我们可以知道：$p$ 质数且 $\gcd(a,p)=1$ ，则 $a^b\equiv a^{b\,\bmod\,(p-1)}\pmod p$ .

三、拓展欧几里得算法

裴蜀定理

对于任意整数 $a,b$ ，存在一对整数 $x,y$ ，满足 $ax+by=\gcd(a,b)$ .

应用

求 $ax+by=\gcd(x,y)$ 的解。

int exgcd(int a,int b,int& x,int &y){	if(!b){x = 1 , y = 0; retu000rn a;}	int g = exgcd(b,a%b,x,y);	int t = x; x = y , y = t - a/b * x;	return g;}

对于 $ax+by=c(c\leq\gcd(a,b))$ ，只有 $c=\gcd(a,b)$ .

另外，若 $(x,y)$ 是原方程的解，那么 $(x\pm\dfrac b{\gcd(a,b)},y\mp\dfrac a{\gcd(a,b)})$ 也是解。

四、线性同余方程

形似 $ax\equiv c\pmod b$ 的方程。

结论：当 $\gcd(a,b)|c$ 时， $ax\equiv c\pmod b$ 一定有解。反之，无解。

假设已知其中一个解 $x=x_0$ ，那么该方程在模 $b$ 意义下，有 $\gcd(a,b)$ 个不同的解。其中 $x_i=\Bigg(x_0+i\times \dfrac d{\gcd(a,b)}\Bigg)\bmod b$ 。

五、乘法逆元

如果 $b,p$ 互质，且 $b|a$ ，则存在一个整数 $x$ ，使得 $\dfrac ab\equiv ax\pmod p$ ，那么 $x$ 称为 $b$ 在模 $p$ 的意义下的乘法逆元，记作 $b^{-1}$ 。

求法

对于 $p$ 是质数，则可以便捷0地使用费马小定理： $b^{-1}\equiv b^{p-2}\pmod p$ .
对于 $p$ 非质数，可以使用拓展欧几里得解同余式解决： $bx\equiv 1\pmod p\Rightarrow bx+py=1$
可以使用线性求逆元。设 $r=b\bmod p$ ，则对于 $b$ 的逆元，公式为 $b^{-1}=-r^{-1}\times\left\lfloor\dfrac pb\right\rfloor$

for(int i = 1 ; i <= n ; i ++)
	inv[i] = ((p-p/i*inv[p%i])%p+p)%p;

六、中国剩余定理

给定一个方程组：

\[\left\{\begin{matrix} x\equiv a_1\pmod{m_1}\\ x\equiv a_2\pmod{m_20} \\\cdots\\ x\equiv a_n\pmod{m_n} \end{matrix}\right. \]

若 $m_1\cdots m_n$ 两两互质，则必定有解。

设 $M=\prod m_i$ ，$M_i=\dfrac M{m_i}$ ， $t_iM_i\equiv 1\pmod{m_i}$ 。（注意是在模 $m_i$ 下的逆元）

那么，其解为：$\sum\limits_{i=1}^na_iM_it_i$ .

证明

设 $p = \sum\limits_{i=1}^na_iM_it_i$ .

对于方程组的第 $j$ 个式0子：

\[a_iM_it_i\equiv \left\{\begin{matrix}0\pmod {m_j} & ,& i\neq j.&\text{因为}M_i\text{中必有}m_j\text{这个因子}\\ a_i\pmod{m_j}&,&i=j.&\text{因为}M_it_i\equiv 1\pmod{m_i}\end{matrix}\ \right. \]

证毕。

因为 $m_i$ 不一定是质数，所以逆元使用拓展欧几里得解决。

关于中国剩余定理的本质，是构造出 $R_i$ ，使得

\[R_i\equiv\left\{\begin{matrix}1&,&i=k\\ 0&,&i\neq k\end{matrix}\right.\pmod {m_k} \]

ll mul=1,M[N],m[N],a[N],t[N],ans;
ll exg0cd(ll a,ll b,ll& x,ll& y){
	if(!b){x=1,y=0 ;return a;}
	ll g = exgcd(b,a%b,x,y);
	ll t = x; x = y , y = t-a/b*x;
	return g;
}
void CRT(){
	ll b;
	for(int i = 1 ; i <= n ; i ++)
		M[i] = mul / m[i],
		exgcd(M[i],m[i],t[i],b),
		(ans += a[i]*M[i]%mul*t[i]%mul+mul) %= mul;
}
signed main(){
	n = read();
	for(int i = 1 ; i <= n ; i ++)
		m[i] = read(), a[i] = read(),
		mul *= m[i];
	CRT();
	printf("%lld",ans);
}

例题

同余方程

求关于 $x$ 的同余方程 $a x \equiv 1 \pmod {b}$ 的最小正整数解。

保证有解。

题解

来自前面的结论：当 $\gcd(a,b)|1$ 时原方程一定有解。且有 $\gcd(a,b)$ 个不同的解。

对于此题，将式子化为 $ax+by=1$ ，即为求 $ax+by=\gcd(a,b)$ 的 $x$ ，因为仅有一解，所以它就是最小整数解。

约数之和

求 $A^B$ 的所有约数之和 $\bmod9901$ 。

题解

$A$ 的所有约数之和为 $\prod \limits_{i=1}^m\begin{pmatrix}\sum\limits_{j=0}^{c_i} (p_i)^j\end{pmatrix}$ 。

那么 $A^B$ 的所有约数之和为 $\prod \limits_{i=1}^m\begin{pmatrix}\sum\limits_{j=0}^{\color{red}{B}c_i} (p_i)^j\end{pmatrix}$ 。

用等比数列展开一下，就是 $\prod \limits_{i=1}^m\begin{pmatrix}\dfrac{p_i^{Bc_i+1}-1}{p_i-1}\end{pmatrix} \bmod 9901$

对于累乘内的式子，我们要考虑它是否可以逆元求。

当 $\gcd(p_i-1,9901)=1$ 时，可以直接用费马小定理逆元求这一项。

否则，因为 $9901$ 是质数，那么 $9901|p_i-1$ 必定成立。

我们设 $t=p_i-1$ ，则 $p_i=t+1$ ，$9901|t$。

原始相当于转化为：求 $\sum\limits_{j=0}^{Bc_i} (t+1)^j\bmod 9901$ 。

$(t+1)^j$ ，展开后对 $9901$ 取模，答案一定为 $1$ .

所以此项结果是 $Bc_i+1$。

signed main(){	a = read(), b = read();	Prime();	for(int i = 1 ; i <= pcnt && a >= pri[i]; i ++){		if(!(a % pri[i])) p[++cnt] = pri[i];		while(!(a % pri[i])) c[cnt] ++, a /= pri[i];	}	if(a > 1) p[++cnt] = a, c[cnt] = 1;	ll ans = 1;	for(int i = 1 ; i <= cnt ; i ++)		if((p[i]-1) % mod) (ans *= (qpow(p[i],b*c[i]+1)-1) * qpow(p[i]-1,mod-2) % mod) %= mod;		else (ans += b*c[i]+1) %= mod;	printf("%lld",ans);}

合法序列

给你一个长度为 $N$ 的正整数序列，如果一个连续的子序列，子序列的和能够被 $K$ 整除，那么就视此子序列合法，求原序列包括多少个合法的连续子序列？

题解

对于一个连续子序列 $[l,r]$ ，其和能被 $K$ 整除，即为 $sum_r \equiv sum_{l-1}\pmod K$ 。

用栈记录即可。

	memset(stk,0,sizeof(stk));	stk[0] = 1;	k = read(), n = read();	for(int i = 1 ; i <= n ; i ++)		sum[i] = (sum[i-1] + read()) % k,		stk[sum[i]] ++;	ll ans = 0;	for(int i = 0 ; i < k ; i ++)		ans += (stk[i]-1)*stk[i] >> 1;	printf("%lld\n",ans);

青蛙的约会

有两只青蛙，青蛙 A 和青蛙 B，他们在同一条经纬线上。他们将同时出发，沿着经纬线先西跳。规定纬度线上东经 $0$ 度处为原点，由东往西为正方向，单位长度 $1$ 米，这样我们就得到了一条首尾相接的数轴。设青蛙A的出发点坐标是 $x$ ，青蛙 B 的出发点坐标是 $y$ 。青蛙 A 一次能跳 $m$ 米，青蛙 B 一次能跳 $n$ 米，两只青蛙跳一次所花费的时间相同。纬度线总长 $L$ 米。现在要你求出它们跳了几次以后才会位于同一点。

题解

一道灵活运用同余方程的题。

首先显然有 $x+mt\equiv y+nt\pmod L$ .

移项一下，变成 $(m-n)t\equiv y-x\pmod L$ .

$\Rightarrow a\times l +(m-n)t = y-x$ .

将 $l$ 与 $m-n$ 看作常量，则原式是不定方程。

已知： $ax+by\equiv c$ ，当且仅当 $\gcd(a,b)| c$ 时有解。

所以原式先判断是否有解。

若有解，则要求最小整数解。

根据同余方程的结论，若 $(x,y)$ 是原方程的解，那么 $(x\pm\dfrac b{\gcd(a,b)},y\mp\dfrac a{\gcd(a,b)})$ 也是解。

于是我们可以用这个方式得到原式的最小整数解。

ll exgcd(ll a,ll b,ll& x,ll& y){
	if(!b){x = 1 , y = 0; return a;}
	ll g = exgcd(b,a%b,x,y);
	ll t = x; x = y , y = t- a/b * x;
	return g;
}
signed main(){
	ll x = read(), y = read(), m = read(), n = read(), l = read();
	if(m < n) swap(n,m), swap(x,y);
	ll a,t;
	ll g = exgcd(l,m-n,a,t);
	if((y-x) % g) puts("Impossible");
	else printf("%lld",((t*(y-x)/g)%(l/g)+l/g)%(l/g));
}

总结

同余中有很多重要的结论与定理。需熟练掌握。

另外，同余方程与不定方程求解也是比较重要的内容。这方面仍需多加练习。

3.组合数学

概念

一、加法、乘法原理

加法原理：完成一个工程可以有 $n$ 类办法， $a_i$ 代表第 $i$ 类方法的数目。那么完成这件事共有 $S=\sum\limits_{i=1}^n a_i$ 种不同的方法。

乘法原理：完成一个工程可以有 $n$ 类办法， $a_i$ 代表第 $i$ 类方法的数目。那么完成这件事共有 $S=\prod\limits_{i=1}^n a_i$ 种不同的方法。

二、排列数与组合数

排列数：从 $n$ 个不同元素中，任取 $m$ 个元素按一定顺序排成一列，用 $\mathrm A_n^m$ 表示。

\[\mathrm A_n^m = n(n-1)(n-2)\cdots(n-m+1)=\dfrac{n!}{(n-m)!} \]

公式的理解：选取 $m$ 个数，第 $1$ 个数有 $n$ 种可选，第 $2$ 个数有 $(n-1)$ 种可选，……，第 $m$ 个数有 $(n-m+1)$ 种可选，运用乘法原理得到公式。

全排列： $\mathrm A_n^m = n!$ ，表示 $n$ 个数的全排列个数。

组合数：从 $n$ 个不同元素中，任取 $m$ 个元素按组成一个集合。用 $\mathrm C_n^m$ 表示。

\[\mathrm C_n^m=\dfrac {\mathrm A_n^m}{m!}=\dfrac{n!}{m!(n-m)!} \]

公式的理解：组成无序的集合，然后进行“全排列”，相当于排成一列。故 $\mathrm C_n^m\times m!=\mathrm A_n^m$ 。

$\mathrm C_n^m$ 还可以表示为 $\begin{pmatrix}n\\m\end{pmatrix}$ 。

三、二项式定理

二项式定理阐明了一个展开式的系数：

\[(a+b)^n=\sum_{i=0}^n \begin{pmatrix}n\\i\end{pmatrix} a^ib^{n-i} \]

公式的理解：将 $(a+b)^n$ 拆开为 $(a+b)(a+b)\cdots(a+b)$ 。对于含有 $a^i$ 的一项，相当于从 $n$ 个因数中选取 $i$ 个取 $a$ ，有 $\begin{pmatrix} n\\i\end{pmatrix}$ 种选取方式。另外，另 $n-i$ 项必定选取 $b$ 。

四、组合数的性质

$\begin{pmatrix}n\\m\end{pmatrix}=\begin{pmatrix}n-m\\m\end{pmatrix}$

从 $n$ 中选 $m$ 个，等价于从 $n$ 中剩 $n-m$ 个。

$\begin{pmatrix}n\\m\end{pmatrix}=\dfrac nm\begin{pmatrix}n-1\\m-1\end{pmatrix}$

$\begin{pmatrix}n\\m\end{pmatrix}=\begin{pmatrix}n-1\\m-1\end{pmatrix}+\begin{pmatrix}n-1\\m\end{pmatrix}$

递推式，可以理解成：已知从 $n-1$ 个数里选取的方案。考虑新加入一个数，若选取这个数，则相当于在原 $n-1$ 个数中选取 $m-1$ 个；若不选取这个数，则相当于在原 $n-1$ 个数中选取 $m$ 个。

五、卢卡斯定理

对于求组合数对质数取模，有：

\[\mathrm C_n^m\equiv \mathrm C_{n\ \bmod\ p}^{m\ \bmod\ p} \times\mathrm C_{\left\lfloor \tfrac np\right\rfloor}^{\left\lfloor \tfrac mp\right\rfloor} \pmod p \]

inline ll C(int n,int m){return n >= m ? fac[n]*ifac[m]%mod*ifac[n-m]%mod : 0;}
ll lucas(int n,int m){
	if(!m) return 1;
	return C(n%mod,m%mod)*lucas(n/mod,m/mod) % mod;
}

例题

古代猪文

iPig 在大肥猪学校图书馆中查阅资料，得知远古时期猪文文字总个数为 $n$ 。当然，一种语言如果字数很多，字典也相应会很大。当时的猪王国国王考虑到如果修一本字典，规模有可能远远超过康熙字典，花费的猪力、物力将难以估量。故考虑再三没有进行这一项劳猪伤财之举。当然，猪王国的文字后来随着历史变迁逐渐进行了简化，去掉了一些不常用的字。

iPig 打算研究古时某个朝代的猪文文字。根据相关文献记载，那个朝代流传的猪文文字恰好为远古时期的 $\frac 1k$ ，其中 $k$ 是 $n$ 的一个正约数（可以是 $1$ 或 $n$）。不过具体是哪 $\frac 1k$，以及 $k$ 是多少，由于历史过于久远，已经无从考证了。

iPig 觉得只要符合文献，每一种 $k|n$ 都是有可能的。他打算考虑到所有可能的 $k$ 。显然当 $k$ 等于某个定值时，该朝的猪文文字个数为 $\frac nk$。然而 $n$ 个文字中保留下 $\frac nk$ 个的情况也是相当多的。iPig 预计，如果所有可能的 $k$ 的所有情况数加起来为 $p$ 的话，那么他研究古代文字的代价将会是 $g^p$。

现在他想知道猪王国研究古代文字的代价是多少。由于 iPig 觉得这个数字可能是天文数字，所以你只需要告诉他答案除以 $999911659$ 的余数就可以了。

$1\le n,g \le 10^9$ .

简化题面

求$g^{\sum\limits_{i|n}\mathrm C^i_n}\pmod{999911659}$。

题解

数论大杂烩题啊……

分为以下步骤来进行：

根据欧拉定理的推论，$\begin{matrix}g^{ \sum\limits_{i|n}\mathrm C^i_n}\pmod{999911659} & = & g^{ \sum\limits_{i|n}\mathrm C^i_n\pmod{\varphi(999911659)}}\pmod{999911659} \\ & = & g^{ \sum\limits_{i|n}\mathrm C^i_n\pmod{999911658}}\pmod{999911659}\end{matrix}$ .
对于这个式子，我们可以先求 \sum\limits_{i|n}\mathrm C^i_n\pmod{999911658} $，再用快速幂来解决。
因为 $n\leq 10^9$ ，枚举其所有因数复杂度必定可行，所以先求出 $n$ 的所有因数。
因为模数 $999911658$ 不是质数，所以求 $\mathrm C_n^i$ 不可以使用逆元。
有 4. 的限制，我们不得考虑：
- 将模数 $999911658$ 分解质因数为 $2\times3\times4679\times35617$ .
- 分别计算 $$\mathrm C_n^i$$ 对于模上述的四个质数条件下的值。
- 对于得到的四个值，等价于给定四个同余方程。
使用中国剩余定理来求这个确定的 $\sum\limits_{i|n}\mathrm C^i_n\pmod{999911658} $ .

ll n,g;
ll fac[N],ifac[N];
ll b[M] = {0,2,3,4679,35617};
ll qpow(ll a,int b,ll p){
    ll ret = 1;
    while(b){
        if(b & 1) (ret *= a) %= p;
        (a *= a) %= p, b >>= 1;
    }
    return ret;
}
ll a[M],m[M],t[M];
ll c[N],cnt;
inline ll C(int n,int m,ll p){return n >= m ? fac[n]*ifac[m]%p*ifac[n-m]%p : 0;}
ll lucas(int n,int m,ll p){
	if(!m) return 1;
	return C(n%p,m%p,p) * lucas(n/p,m/p,p) % p;
}

void work(int x){
    ll p = b[x];
    ifac[0] = fac[0] = 1;
    for(int i = 1 ; i < p ; i ++) fac[i] = fac[i-1] * i % p;
    ifac[p-1] = qpow(fac[p-1],p-2,p);
    for(int i = p-2 ; i ; i --) ifac[i] = ifac[i+1] * (i+1) % p;
    for(int i = 1 ; i <= cnt ; i ++) (a[x] += lucas(n,c[i],p)) %= p;
}
ll CRT(){
	ll mul = 1, ret = 0;
	for(int i = 1 ; i <= 4 ; i ++) mul *= b[i];
	for(int i = 1 ; i <= 4 ; i ++) m[i] = mul / b[i],
		t[i] = qpow(m[i],b[i]-2,b[i]);
    for(int i = 1 ; i <= 4 ; i ++)
		(ret += a[i]*m[i]*t[i]) %=  mul;
	return ret;
}
signed main(){
    n = read(), g = read();
    if(!(g % mod)) return puts("0"), 0;
    int ed = sqrt(n);
	for(int i = 1 ; i <= ed ; i ++)
		if(!(n % i))
			c[++cnt] = i,
			c[++cnt] = n/i;
	if(ed*ed == n) cnt --;
    for(int i = 1 ; i <= 4 ; i ++) work(i);
    ll ans = CRT();
    printf("%lld",qpow(g,ans,mod));
    return 0;
}

临时笔记

Miller-Rabin素数

积性函数：单位函数、常数1、约数个数函数、约数和函数、欧拉函数

快速幂b=b%(p-1);

未完。

posted @ 2021-09-26 00:09 Last-Order 阅读(298) 评论(0) 编辑收藏举报

刷新页面返回顶部

Shinomiya