【YBTOJ】【单调队列优化DP】写博客
写博客
小泽发了一篇博客,由 \(n\) 个小写英文字母组成,由于包含违禁词,被自动隐藏。
具体地,违禁词有 \(m\) 个,分别为 \(T_1,T_2,\dots,T_m\) 。
小泽发现,只要博客中,连续地包含了其中违禁词,那么博客就会被自动隐藏。换言之,对于任意 \(1\leq i\leq m\) , \(T_i\) 都不能是最终发表的博客 \(S\) 的子串。
于是小泽决定在原来的博客 \(S\) 上把一部分字母替换成空格,使得它不再包含违禁词。如果她把第 \(i\) 个字母替换成空格,与之相邻的两个字母将不会连续,但是整篇博客的价值会减少 \(a_i\) 。
小泽想要知道,如何替换可以得到一篇不会被自动隐藏的博客,而价值的减少量最少。请你帮她回答这个问题。
\(1\leq n=|S|\leq2\times10^5\) , \(1\leq m\leq10\) , \(1\leq|T_i|\leq2\times10^5\) , \(0\leq a_i\leq 1000\).
题解
设原串是 a 串,违禁词串为 b 串。
将 b 串在 a 串内跑kmp,找到每个 b 串在 a 串中出现的位置(设为线段\((l,r)\))。
则原问题转化为:选取权值最小的点集,覆盖所有线段。
- 设 \(dp_i\) 表示必定选取点 \(i\) ,且覆盖所有位置在点 \(i\) 及 \(i\) 之前的线段,所用的最小代价。
- 另设 \(pre_i\) 表示严格以 \(i\) 为右端点的所有线段中,左端点最大的线段的左端点值。
如下图,其 \(pre_i\) 为 \(x_2\) .
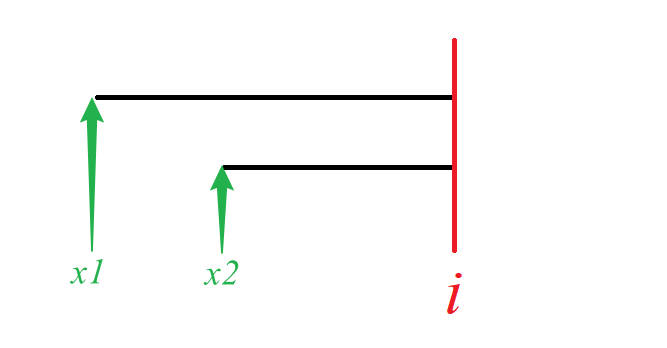
考虑:对于一个 \(dp_i\) ,显然有 \(dp_i=dp_j+w_i\)。
那么, \(j\) 的范围应该是什么?
我们重新考虑 dp 的定义。
\(dp\)表示“覆盖所有位置在点 \(i\) 及 \(i\) 之前的线段”。
拆分此定义来看:
- 覆盖所有在 \(i\) 之前的线段
- 覆盖所有经过 \(i\) 的线段
对于1.,显然是用 \(dp_j\) 覆盖,并转移而来。
对于2.,则是用 \(w_i\) 来覆盖。
形象化地来说,对于下图:
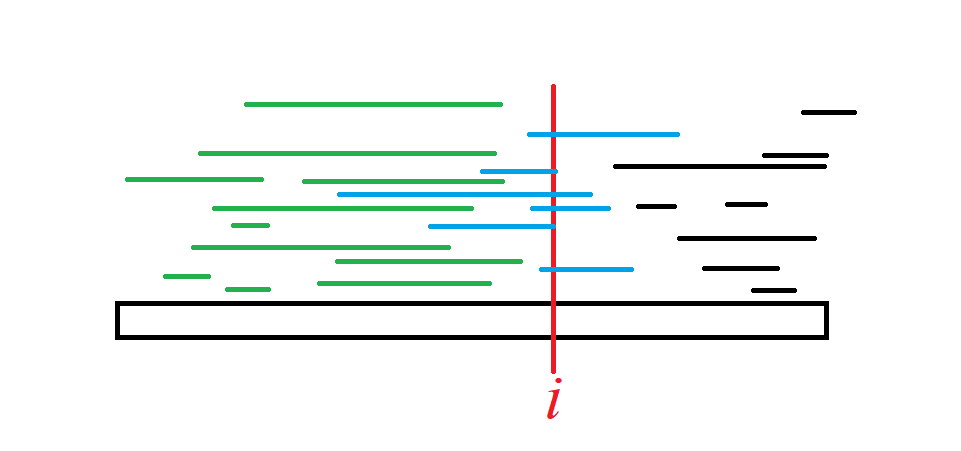
对于点 \(i\) ,其左侧所有绿色线段由 \(dp_j\) 来覆盖,经过它的所有蓝色线段由 \(i\) 来覆盖,右侧黑色线段暂不考虑。
除去一些线段,得到如下:

对于点 \(i-1\) ,有一条线段经过它,其左端点为\(pre_{i-1}\)。
使用 \(dp_{j}\) 来覆盖绿色线段时,必定要让 \(j\) 来覆盖掉所有在 \([pre_{i-1},i-1]\) 之间的线段。
由此可知,\(j\in[pre_{i-1},i-1]\).
总 DP 式: \(dp_i = \min\limits_{j=pre_{i-1}}^{i-1}\{dp_j\}+w_i\).
显然,强制使 \(pre\) 单调不降后,答案必定成立。
这样,可以使用单调队列来优化 dp .
关于为什么 \(j\) 的左端点不可取 \(pre_i\):
- 由于点 \(i\) 表示右端点是 \(i\) 的线段,这些线段会被 \(i\) 覆盖,而不是 \(j\) .
代码
#include <bits/stdc++.h>
#define fo(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout);
using namespace std;
const int INF = 0x3f3f3f3f,N = 2e5+5;
typedef long long ll;
typedef unsigned long long ull;
inline ll read(){
ll ret=0;char ch=' ',c=getchar();
while(!(c>='0'&&c<='9'))ch=c,c=getchar();
while(c>='0'&&c<='9')ret=(ret<<1)+(ret<<3)+c-'0',c=getchar();
return ch=='-'?-ret:ret;
}
int n,m,w[N];
template <typename T> struct dque{
T a[N]; int st=1,ed=0;
dque(){st=1,ed=0;}
inline void clear(){st=1,ed=0;}
inline int size(){return ed-st+1;}
inline bool empty(){return !(ed-st+1);}
inline void pop_front(){st++;}
inline void pop_back(){ed--;}
inline T front(){return a[st];}
inline T back(){return a[ed];}
inline void push_back(T x){a[++ed] = x;}
inline T operator [] (int x){return a[st+x-1];}
};
int fail[N],pre[N];
void kmp(char a[],char b[]){
int len = strlen(b+1);
memset(fail,0,sizeof(int)*(len+1));
for(int i=2,j=0 ; i <= len ; i ++){
while(j && b[j+1] != b[i]) j = fail[j];
j += b[j+1] == b[i];
fail[i] = j;
}
for(int i=1,j=0 ; i <= n ; i ++){
pre[i] = max(pre[i],pre[i-1]);
while(j && b[j+1] != a[i]) j = fail[j];
j += b[j+1] == a[i];
if(j == len) pre[i] = max(pre[i],i-len+1) , j = fail[j];
}
}
char a[N],b[N];
int dp[N];
signed main(){
n = read() , m = read();
scanf("%s",a+1);
for(int i = 1 ; i <= n ; i ++)
w[i] = read();
while(m--){
scanf("%s",b+1);
kmp(a,b);
}
dque<int> q;
q.push_back(0);
n++;
for(int i = 1 ; i <= n ; i ++){
while(!q.empty() && q.front() < pre[i-1]) q.pop_front();
dp[i] = dp[q.front()] + w[i];
while(!q.empty() && dp[q.back()] > dp[i]) q.pop_back();
q.push_back(i);
}
printf("%d",dp[n]);
return 0;
}

