【YBTOJ】【状压DP】最优组队(枚举子集)
最优组队
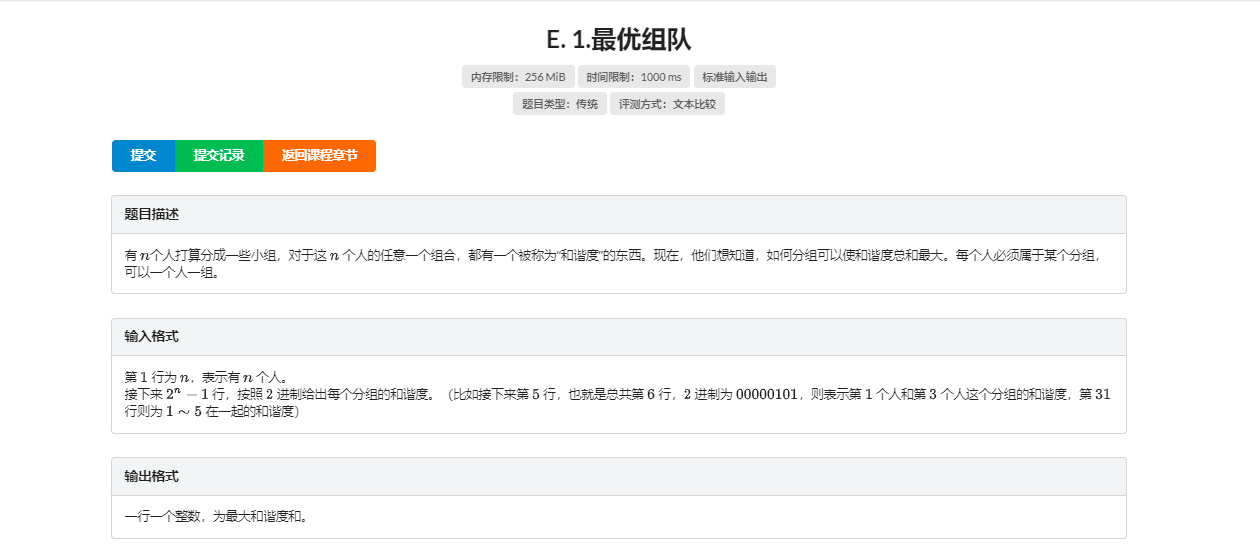
\(n\le 16\)
题解
看到数据范围,肯定是状压 DP .
很快有一个思路:对于每个状态,枚举其子集,进行求 Max.
有如下代码:
#include <bits/stdc++.h>
#define fo(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout);
using namespace std;
const int INF = 0x3f3f3f3f,N = 18,M = 1<<N;
typedef long long ll;
typedef unsigned long long ull;
inline ll read(){
ll ret=0;char ch=' ',c=getchar();
while(!(c>='0'&&c<='9'))ch=c,c=getchar();
while(c>='0'&&c<='9')ret=(ret<<1)+(ret<<3)+c-'0',c=getchar();
return ch=='-'?-ret:ret;
}
int n,m;
int dp[M];
signed main(){
n = read();
m = (1<<n) - 1;
for(int i = 1 ; i <= m ; i ++)
dp[i] = read();
for(int i = 1 ; i <= m ; i ++)
for(int j = 1 ; j <= i ; j ++)
if((i|j) == i)
dp[i] = max(dp[i],dp[j] + dp[i^j]);
printf("%d",dp[m]);
}
但是它 30 分 TLE 了。
分析其复杂度:枚举状态 \(O(2^n)\) ,枚举其子集又是 \(O(2^n)\) ,总复杂度 \(O(2^{2n})=O(4^n)\) .
优化
从书上发现一种枚举子集的方法:while(sub) sub = (sub-1) & S;
使用此方法,可以不重不漏地枚举出 \(S\) 的子状态。
【证明】由 \(sub = (sub-1)\ \And\ S\) 可知 \(sub\) 每次会变小。那么我们证明区间 \(\begin{pmatrix}(sub-1)\ \And\ S &,&sub\end{pmatrix}\) 中不存在 \(S\) 的子集。设 \(sub=\begin{pmatrix}d_1d_2\cdots d_k10\cdots0\end{pmatrix}_2\) ,则 \(sub-1=\begin{pmatrix}d_1d_2\cdots d_k01\cdots1\end{pmatrix}_2\) 。由于 \(sub\) 是 \(S\) 的子集,那么 \(sub-1=\begin{pmatrix}d_1d_2\cdots d_k00\cdots0\end{pmatrix}_2\) 也是 \(S\) 的子集。因此考虑 \(sub-1=\begin{pmatrix}d_1d_2\cdots d_k01\cdots1\end{pmatrix}_2\ \And\ S\) ,得到的一定是 \(\begin{pmatrix}d_1d_2\cdots d_k00\cdots0\end{pmatrix}_2\) 与 \(\begin{pmatrix}d_1d_2\cdots d_k10\cdots0\end{pmatrix}_2\) 中值最大的子集。
证毕。
【关于时间复杂度】
对于 \(O(2^n)\) 种状态中每一个状态,都有\(C_n^i\)种子状态。
复杂度:\(O\begin{pmatrix}\sum\limits_{i=1}^n C_n^i\cdot2^i\end{pmatrix}\)。
根据二项式定理:\(O\begin{pmatrix}\sum\limits_{i=1}^n C_n^i\cdot2^i\end{pmatrix} = O\begin{pmatrix}\sum\limits_{i=1}^n C_n^i\cdot2^i\cdot 1^{n-i}\end{pmatrix} = O\begin{pmatrix}(1+2)^n\end{pmatrix}\).
故复杂度:\(O(3^n)\).
代码
#include <bits/stdc++.h>
#define fo(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout);
using namespace std;
const int INF = 0x3f3f3f3f,N = 18,M = 1<<N;
typedef long long ll;
typedef unsigned long long ull;
inline ll read(){
ll ret=0;char ch=' ',c=getchar();
while(!(c>='0'&&c<='9'))ch=c,c=getchar();
while(c>='0'&&c<='9')ret=(ret<<1)+(ret<<3)+c-'0',c=getchar();
return ch=='-'?-ret:ret;
}
int n,m;
int dp[M];
signed main(){
n = read();
m = (1<<n) - 1;
for(int i = 1 ; i <= m ; i ++)
dp[i] = read();
for(int i = 1 ; i <= m ; i ++){
int j = i;
while(j){
j = (j-1)&i;
dp[i] = max(dp[i],dp[j] + dp[i^j]);
}
}
printf("%d",dp[m]);
}

