计算机无法精确存储小数！
题目链接：Dollars UVA - 147
历程
在洛谷上练习DP时，遇到两道题：UVA674 Coin Change和UVA147 Dollars。两道题都是完全背包统计方案数类型，且基本一模一样。双倍经验
其中：第一题Coin Charge的难度评级为普及/提高-，而Dollars的难度评级为提高+/省选-。看了一下两道题，写完基本一样的代码后直接提交。Coin Change轻松AC，但Dollars一直WA。
检查 半个小时 后，发现问题：
int(x * 100)表达式，当\(x=1.15\)时，\(x\times100\)为\(115.0\)，但转为int后却为\(114\)。
于是便引出今天的问题：计算机的精度。
正题
一般计算机可以有十几位甚至几十位（二进制）有效数字，计算精度可由千分之几到百万分之几，是任何计算工具所望尘莫及的。（来自百度百科）
计算机存储小数的流程
- 第一步：转换成二进制
- 第二步：用二进制科学计算法表示
- 第三步：表示成 IEEE 754 形式
在上面的第一步和第三步都有可能 丢失精度。\(^{[1]}\)
无限循环小数的存储
考虑在10进制下将\(\frac17\)写成小数。
用 1 除以 7，得到的商就是小数部分，剩下的余数我们继续除以 7，一直除到什么时候结束呢？ 有两种情况：
- 如果余数为 0。结束。
- 如果不为0，继续除下去（\(3,2,6\cdots\)）
- 当除到某一步时，余数等于 1。此时再继续除下去，就又是 \(\frac17\) 了。绕了几圈又回到\(1\div7\)了。
注意3：我们判断他循环，并不是从直观看感觉它重复了，而是因为 在计算过程中，它又回到了开头。
因此：循环小数不能精确表示，放到计算机中会丢失精度； 那么有限小数可以精确表示吧，比如 0.1。
无限循环小数的存储
例如\(\pi\approx3.14159\cdots\)，\(e\approx2.71828\cdots\)，……，这些数显然无法精确存储。
有限小数的存储\(^{[2]}\)
我们按照乘以 2 取整数位的方法，把 0.1 表示为二进制
(1) 0.1 x 2 = 0.2 取整数位 0 得 0.0
(2) 0.2 x 2 = 0.4 取整数位 0 得 0.00
(3) 0.4 x 2 = 0.8 取整数位 0 得 0.000
(4) 0.8 x 2 = 1.6 取整数位 1 得 0.0001
(5) 0.6 x 2 = 0.2 取整数位 1 得 0.00011
(6) 0.2 x 2 = 0.4 取整数位 0 得 0.000110
(7) 0.4 x 2 = 0.8 取整数位 0 得 0.0001100
(8) 0.8 x 2 = 1.6 取整数位 1 得 0.00011001
(9) 0.6 x 2 = 1.2 取整数位 1 得 0.000110011
(n) ...
我们得到一个无限循环的二进制小数 0.000110011…
因此，0.1不能在计算机内精确存储。
0.1 到 0.9 的 9 个小数中，只有 0.5 可以用二进制精确的表示。
如果把 0.0 再算上，那么就有两个数可以精确表示，一个奇数 0.5，一个偶数 0.0。
回到历程中的问题：
double下的\(115.0\)，可能输出时显示\(115.0\)，但由于无法精确存储，可能存入的数字在十进制下为\(114.99\cdots9\)，转为int时取整导致错误
有什么用？
因为本人目前才疏学浅，不知道了解这个有什么用……但是突然发现了感觉很有趣，于是就写了篇博客记录一下。
在后续关于可能涉及精度的问题，可以使用四舍五入:
int(a)
↓↓↓↓↓↓↓↓↓↓
int(a+0.5)
另外：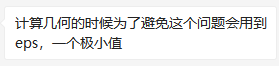
\(^{[3]}\)
参考： [1][2]代码之谜（五）- 浮点数（谁偷了你的精度？）
一位机房大佬：忘怀星 的个人中心
