P1242 新汉诺塔 题解
原题链接

本题解参考:https://www.luogu.com.cn/blog/maoxiaozhukai/solution-p1242,并压行优化
思路
调了一晚上的题…………
首先思考:策略要将盘子从大到小移动(显然成立)
但在移动大的盘子时,需要先将它上面的盘子都先移动走。
假设当前需处理的最大的盘子为\(n\),需要将\(n\)由\(\operatorname{A}\)移动到\(\operatorname{C}\),则可能有两种(最简)情况:
- 把所有比\(n\)小的都移动到\(\operatorname{B}\)盘上,再将\(n\)移动到\(\operatorname{C}\);
- 把所有比把所有比\(n\)小的都移动到\(\operatorname{C}\)盘上,再将\(n\)移动到\(\operatorname{B}\),将所有比\(n\)小的都移动到\(\operatorname{A}\)盘上,最后将\(n\)移动到\(\operatorname{C}\)。
第二种看似比较麻烦,但是用另一种方法理解:\(n\)移走后空出了\(\operatorname{A}\)盘的位置,这样所有比\(n\)小的部分只需要进行一次移动即可。而第一种在此时需要将所有比\(n\)小的部分移动两次,显然第二种比第一种更简单。
如果还没看懂,看如下举例:

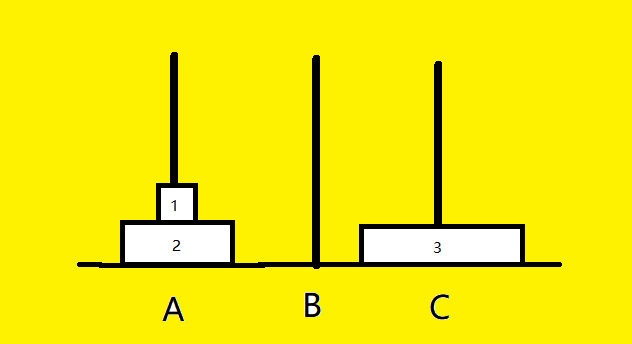
由上图,要将原图(白)移动为移后图(黄),则:
方法1为:\(1:C\rightarrow A,\quad2:C\rightarrow B,\quad1:A\rightarrow B,\quad3:A\rightarrow C,\quad1:B\rightarrow C,\quad2:B\rightarrow A,\quad1:C\rightarrow A\)
操作次数为\(7\);
方法2为:\(3:A\rightarrow B,\quad1:C\rightarrow B,\quad2:C\rightarrow A,\quad1:B\rightarrow A,\quad1:A\rightarrow C\)
操作次数为\(5\);
所以可以分为2种情况。
而第二种做法仅在第一步与第一种做法不同,其余相同,则第二种做法只需特别处理第一步即可。
另外关于中转塔的问题:设\(A、B、C\)塔编号分别为\(1,2,3\),三个塔编号之和为\(6\),找非起点也非终点的塔编号,即为\(6-[起点编号]-[终点编号]\)。
代码
#include <bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f,N = 46;
int now[3][N],to[N];//开二维数组替代三个一维数组,每一维表示一次分类,如[1]为方法1,[2]为方法2,[0]为结果
int ans[3];//分别存储三个答案
void dfs(int i,int _fr,int _to,int tp,bool ot){
//分别表示:当前盘的编号,盘起点,盘终点,分类方式,是否要输出
if(now[tp][i] == _to)return;//边界条件:如果在当前维下的第i个盘已经到达终点就回溯
if(i == 1){//第一个盘直接"移动并输出"即可
now[tp][i] = _to;//将当前维下的第i个盘移动到它的位置
if(ot)printf("move %d from %c to %c\n",i,_fr+'A'-1,_to+'A'-1);//用ot来控制是否输出
ans[tp]++;//当前维下的答案+1
return;
}
for(int j = i - 1 ; j >= 1 ; j --)
if(now[tp][j] != 6-_fr-_to)
dfs(j,now[tp][j],6-_fr-_to,tp,ot);//列举,如果比它编号小的盘不在中转塔位置上,则此盘一定“挡路”,进行深搜并移走它
now[tp][i] = _to;//与上同理
if(ot)printf("move %d from %c to %c\n",i,_fr+'A'-1,_to+'A'-1);
ans[tp]++;
}
int main(){
int n,x,m;
scanf("%d",&n);
for(int i = 1 ; i <= 3 ; i ++){//输入每个盘的起点
scanf("%d",&m);
for(int j = 1 ; j <= m ; j ++){
scanf("%d",&x);
now[0][x] = now[1][x] = now[2][x] = i;
}
}
for(int i = 1 ; i <= 3 ; i ++){//输入每个盘的终点
scanf("%d",&m);
for(int j = 1 ; j <= m ; j ++){
scanf("%d",&x);
to[x] = i;
}
}
for(int i = n ; i >= 1 ; i --)//查询第一种方法所用的答案
if(now[1][i] != to[i])
dfs(i,now[1][i],to[i],1,0);
{//查询第二种方法所用的答案
for(int i = n ; i >= 1 ; i --)
if(now[2][i] != to[i]){
dfs(i,now[2][i],6-now[2][i]-to[i],2,0);
break;//处理第一步,将其转到中转塔上
}
for(int i = n ; i >= 1 ; i --)
if(now[2][i] != to[i])
dfs(i,now[2][i],to[i],2,0);//剩下与第一种相同
}
if(ans[1] < ans[2]){//最后判断使用哪种
for(int i = n ; i >= 1 ; i --)
if(now[0][i] != to[i])
dfs(i,now[0][i],to[i],0,1);
}
else{
for(int i = n ; i >= 1 ; i --)
if(now[0][i] != to[i]){
dfs(i,now[0][i],6-now[0][i]-to[i],0,1);
break;
}
for(int i = n ; i >= 1 ; i --)
if(now[0][i] != to[i])
dfs(i,now[0][i],to[i],0,1);
}
printf("%d",ans[0]);
return 0;//愉快地结束
}
当然以上代码还可以继续简化。
若发现错误请指出!感谢各位!

