PCA算法
1.正交投影
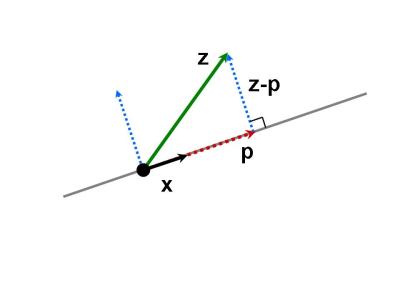
向量$z$投影在$x$向量上的投影向量为$p$,则$z-p$垂直于$x$,有$<z-p, x> = 0$.
令$p=kx$, 根据内积为0,有$x^T(z-kx)=0$,
故得到$ k = \frac{x^Tz}{x^Tx}$,$p=kx = \frac{x^Tz x}{x^Tx} = \frac{xx^Tz}{x^Tx}$.
一般称$P=\frac{xx^T}{x^Tx}$为投影矩阵。
2.拓展到高维,比如三维空间。

对于将三维空间中向量$x$投影到一个平面上,设平面的两个基分为$a_1,a_2$,矩阵$A=[a_1,a_2]$, 容易得到投影后的向量$p=c_1 a_1 + c_2 a_2 = A c$.
其中$c=\begin{bmatrix} c_1\\ c_2 \end{bmatrix}$。
为了求投影,就是为了求$c$。容易有$<x-Ac, a1> = 0, <x-Ac,a2>=0$,有:
$\begin{bmatrix} {a_1}^T\\ {a_2}^T \end{bmatrix} (x-Ac) = \begin{bmatrix} 0\\ 0 \end{bmatrix}$,即 $A^T (x-Ac) = 0$:
有, $A^TAc = A^Tx\\ c= (A^TA)^{-1} A^T x$ 。
故$x$ 在平面上的投影为$p = Ac = A(A^TA)^{-1} A^T x$,一般称 $P=A(A^TA)^{-1} A^T $为投影矩阵。
当平面的两个基$a_1,a_2$标准正交时,则有投影为$p = Ac = AA^T x$,投影矩阵为$P= AA^T$。
3.讲完投影,开始讲PCA算法。PCA是一种降维算法,目的是将一个高维的向量$x\in R^D$用更低维的向量$\hat{x} \in R^M$来表示。
3.1假设估计的$\hat{x} = \sum_{j=1}^{M} \beta_{jn} b_{j}$,
其中$b_j, j= 1.,..,M$ 为低维空间中的一组标准正交基.
$J = \frac{1}{N} \sum_{n=1}^N \|x-\hat{x} \| ^2 $ ,其中$N$为样本个数。
3.2为了寻找合适的$\beta_{jn}$,使得误差$J$最小, 需要对$J$求导数。
$\frac{\partial{J}}{\partial{\hat{x}}} = - \frac{2}{N} (x_n - \hat{x_n})^T$
$ \frac{\partial{J}}{ \partial{\beta_{jn}}} = \frac{\partial{J}}{\partial{\hat{x_n}}} \frac{\partial{\hat{x_n}}}{\partial{\beta_{jn}}}$,
其中$\frac{\hat{x_n}}{\partial{\beta_{in}}} = b_j, j = 1, ..., M$。
当满足$\frac{J}{\beta_{jn}} = 0$时,我们可以认为找到了最合适的基坐标,或者说是基稀疏,使得误差$J$最小。
即$\frac{\partial{J}}{\partial{\beta_{jn}}} = - \frac{2}{N} (x_n-\hat{x_n})^T b_j $
$=-\frac{2}{N} (x_n - \sum_{i=1}^M \beta_{in}b_i )^T b_j $
$=-\frac{2}{N}({x_n}^T b_j - \beta_{jn}) = 0$
故我们得到$\beta_{jn} = {x_n}^T b_j $,即最优的$\beta_{jn}$是$x_n$在$b_j$上的投影长度。
3.3假设我们主成分空间的基为$b_1...b_M$,
可以得到:
$x_n = \sum_{j=1}^{M}\beta_{jn}b_j$
$=\sum_{j=1}^M {x_n}^T b_j b_j$
$=\sum_{j=1}^{M}b_j {b_j}^T x_n $
$=(\sum_{j=1}^{M})b_j {b_j}^T)x_n$
其中$(\sum_{j=1}^{M})b_j {b_j}^T)$为投影矩阵。
原来的数据$x_n = \sum_{j=1}^{M} (b_j {b_j}^T ) x_n + \sum_{j=M+1}^{D}b_j {b_j}^Tx_n$
故有$(x_n - \hat{x}) = \sum_{j=M+1}^D b_j {b_j}^T x_n$
$J= \sum_{j=M+1}^{D}b_j {b_j}^Tx_n = \sum_{j=M+1}{D} {b_j}^T x_n b_j$
重新写误差函数$J$:
$J = \frac{1}{N} \sum_{n=1}^N {\| x-\hat{x}\|} ^2 $
$ = \frac{1}{N} \sum_{n=1}^N {\|\sum_{j=M+1}^D ({b_j}^T x_n)b_j }^2$
$ = \frac{1}{N} \sum_{n=1}^N \sum_{j=M+1}^D (b_j ^Tx_n) ^2$
$ = \frac{1}{N} \sum_n \sum_j b_j^T x_n x_n^T b_j$
$= \sum_{j=M+1}{D}b_j^T(\frac{1}{N} \sum_{n=1}^Nx_nx_n^T ) b_j $
$= \sum_{j=M+1}^D b_j^T S b_j$
其中$\frac{1}{N} \sum_{n=1}^Nx_nx_n^T$为数据协方差矩阵。
3.4 我们先从二维空间来推导PCA,假设主成分空间的基向量为$b_1$,其正交补空间为$b_2$,假设基向量都是标准正交。
$J = b_2^T S b_2, b_2^T b_2 =1$
构造拉格朗日乘子:
$L= b_2^TSb_2+\lambda(1-b_2^Tb_2)$ ,对$\lambda,b_2$求导数:
$\frac{\partial{L}}{\partial{\lambda}} = 1 - b_2^Tb_2 = 0$
$\frac{\partial{L}}{\partial{b_2}} = 2b_2^TS - 2\lambda b_2^T = 0$
我们得到$Sb_2 = \lambda b_2$,也就说,最佳正交补空间基为S矩阵的特征值$\lambda$对应的特征向量。
$J = b_2^TSb_2 = b_2^T \lambda b_2 = \lambda$,
当缩小$J$即是缩小对应的特征值,也就是说主成分空间的基对应的是特征值大的特征向量。
故拓展到$D$维的时候,有 $J = \sum_{j=M+1}^D\lambda_j, j=M+1, ...,D$
$J = \sum_{j=M+1}^Db_j^T Sb_j = \sum_{j=M+1}^D \lambda_j$
4.总结
综上所述,我们求得的主成分空间为对应于特征值大的特征向量,设
$B = [b_1,b_2...,b_M]$为主成分空间基组成的矩阵,我们最后求得的$\hat{x}$为投影于此主成分空间的投影向量。
有$\hat{x} = B B^Tx$。

