Dijkstra 算法（C++）

一、Dijkstra 算法的基本思想

Dijkstra 算法是解决单源最短路径问题的一般方法，它是一种贪心算法，要求图中所有边的权重非负。它的基本思想是：从一个起始顶点开始向外扩张，持续不断地将生成的图扩展到已知距离和最短路径的区域。简单地说，就是先加入最近的顶点，然后加入更远一些的顶点。

Dijkstra 算法类似广度优先搜索，扩展也是按照阶段进行的。设图的顶点集为 V，边集为 E，已知最短路径的顶点集为 R，（R 是 V 的一个子集） ，起始顶点为 s。在每个阶段，Dijkstra 算法从集合 V-R 中选择最短路径估计最小的顶点 v（在 V-R 中距离 s 最近的顶点），将 v 加入已知区域 R，然后对 v 的邻接点的最短距离进行调整更新（松弛）。

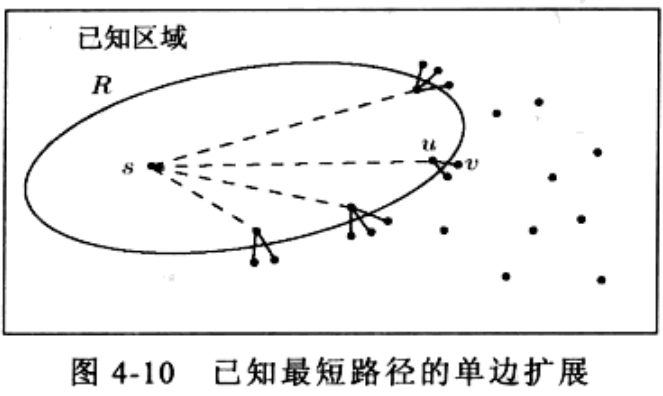
下面给出拓展 R 的伪代码：

二、算法要点

该算法有几个要点。

  1. 图的存储方式。这里使用邻接表较为简单。

    		vector< pair<int, int> > adj[1501];  // adj[i].first为邻接点的编号，adj[i].second为到边距离。

  2. 每个结点需要建立一个结构体

    		struct Vertex
    		{
    		    int index;
    		    int known;
    		    int dist;
    		    int path;
    		    Vertex() : index(-1), known(0), dist(INT_MAX), path(-1) {}
    		};
    		Vertex table[1501];
    • index 为图中结点的编号（可有可无）
    • known 用来标记该节点的最短路径是否已知（true 已知，false 未知）。true 表明该节点属于已知区域 R，false 表明该节点属于 V - R。
    • dist 表示起始顶点 s 到该节点的距离。如果 known 为 true，则 d 为最短距离。
    • path 表示起始顶点 s 到该结点路径中的上一个结点（前驱），它用来打印路径。

  3. 核心部分（参考伪代码写出）

    		void Dijkstra(int start, int n)
    		{
    		    table[start].dist = 0;	// 起始顶点的距离为0。
    		 
    		    for (;;)
    		    {
    		        int k = findmin(n);		// 找到V-R中距离s最近的顶点。
    		        if (k == -1)			// 所有的顶点都已知最短路径了，即V=R。
    		            break;
    		        table[k].known = 1;		// 将该节点加入已知区域R中。
    		 
    		        // 更新当前节点的所有邻接点的最短路径（松弛）
    		        for (int i = 0; i < adj[k].size(); ++i)
    		        {
    		            int v = adj[k][i].first;
    		            if (table[v].known == 0 && table[v].dist > table[k].dist + adj[k][i].second)
    		            {
    		                table[v].dist = table[k].dist + adj[k][i].second;
    		                table[v].path = k;
    		            }
    		            // 如果节点v最短路径未知，且经过当前顶点k的路径，能够使得从源节点s到结点v的最短路径的权重比当前的估计值更小，则我们对结点v的估计值dist和前驱path进行更新。
    		        }
    		    }
    		}

    具体细节在注释。在 main 函数中已经使用 Initiate 进行初始化（其实也不需要，因为 Vertex 类的默认构造函数已经初始化了）。

    对于 findmin，可以使用优先队列，但是本人水平有限，就使用暴力搜索的方式。

    		int findmin(int n)
    		{
    		    int min = INT_MAX, key = -1;
    		    for (int i = 1; i <= n; ++i)
    		    {
    		        if (!table[i].known && table[i].dist < min)
    		        {
    		            min = table[i].dist;
    		            key = i;
    		        }
    		    }
    		 
    		    return key;
    		}

三、时间复杂度

这里我使用了数组来存储结点 dist 的信息，所以 findmin 操作（找到 V-R 中 dist 最小值的顶点）会花费 O(|V|) 时间，松弛操作又花费 O(|E|) 时间，所以运行时间为 O(|V|^2)。
补充：采用不同数据结构时间复杂度

四、测试代码

最后给出测试代码，如果有错请指出。

#include <bits/stdc++.h>
 
using namespace std;
 
vector< pair<int, int> > adj[1501];
 
struct Vertex
{
    int index;
    int known;
    int dist;
    int path;
    Vertex() : index(-1), known(0), dist(INT_MAX), path(-1) {}
};
Vertex table[1501];
 
void Initiate(int n)
{
    for (int i = 1; i <= n; ++i)
    {
        table[i].index = i;
        table[i].known = 0;
        table[i].dist = INT_MAX;
        table[i].path = -1;
    }
    
    for(int i = 1; i <= n; ++i){
        adj[i].clear();
    }
}
 
int findmin(int n)
{
    int min = INT_MAX, key = -1;
    for (int i = 1; i <= n; ++i)
    {
        if (!table[i].known && table[i].dist < min)
        {
            min = table[i].dist;
            key = i;
        }
    }
 
    return key;
}
 
void Dijkstra(int start, int n)
{
    table[start].dist = 0;
 
    for (;;)
    {
        int k = findmin(n);
        if (k == -1)
            break;
        table[k].known = 1;
 
        // 更新当前节点的所有邻接点
        for (int i = 0; i < adj[k].size(); ++i)
        {
            int v = adj[k][i].first;
            if (table[v].known == 0 && table[v].dist > table[k].dist + adj[k][i].second)
            {
                table[v].dist = table[k].dist + adj[k][i].second;
                table[v].path = k;
            }
        }
    }
}
 
void Print(int start, int n){
    for(int i = 1; i <= n; ++i){
        if(table[i].known == 1)
            cout << start << "-" << i << ":" << table[i].dist << endl;
    }
}
 
void print_path(Vertex v) {
    if(v.path != -1) {
        print_path(table[v.path]);
        cout << " to ";
    }
    cout << v.index;
}
 
int main()
{
    int t;
    cin >> t;   // 样例数
    for (int i = 1; i <= t; ++i)
    {
        int n, m;
        cin >> n >> m;      // 顶点数，边数
        Initiate(n);
        int u, v, w;
        for (int i = 1; i <= m; ++i)
        {
            cin >> u >> v >> w;
            adj[u].push_back({v, w});
        }
 
        int src;
        cin >> src;
        Dijkstra(src, n);
        Print(src, n);      // 输出从源点到其他点的最短路径
    }
 
    return 0;
}
输入：
1
100 198
1 40 6
1 88 3
2 16 5
3 51 2
4 36 7
4 64 3
4 81 2
5 94 3
6 8 3
7 63 3
7 87 8
7 99 5
8 32 10
8 51 1
8 64 3
8 66 5
8 71 5
8 98 8
9 12 2
9 40 5
10 31 4
10 45 4
10 55 4
11 24 4
11 63 4
12 46 2
12 81 4
12 97 6
13 24 6
15 47 10
15 83 6
15 100 1
16 54 1
16 71 6
17 51 4
17 90 8
18 70 10
18 96 9
19 67 3
21 47 3
21 93 1
21 99 3
22 36 2
23 21 9
23 30 10
23 74 4
24 89 10
25 71 1
26 5 9
26 33 10
26 47 8
26 73 3
26 97 2
27 67 2
28 96 2
29 64 5
29 81 4
30 96 5
31 1 9
31 35 7
32 81 6
33 21 9
33 100 5
34 4 2
34 59 2
34 68 3
34 95 3
38 24 9
39 7 6
39 14 6
39 45 10
39 90 4
39 92 10
41 71 6
41 95 4
42 43 10
42 52 4
42 62 5
42 64 6
43 9 8
43 65 9
43 66 10
43 96 8
44 13 4
44 22 9
44 61 3
44 81 9
45 52 6
46 26 8
47 28 1
47 52 2
47 70 7
48 31 9
48 33 2
50 32 5
50 43 10
52 43 3
52 83 8
53 1 8
53 4 8
53 33 4
53 41 2
53 59 6
54 58 9
54 88 3
56 39 3
57 2 5
57 23 7
57 44 10
59 19 9
60 82 1
61 22 1
62 20 9
62 74 6
63 21 8
63 98 3
64 9 2
64 50 8
65 73 3
66 24 4
66 44 4
67 20 10
67 34 7
67 68 8
67 72 8
67 83 8
67 98 8
68 8 6
68 25 7
68 67 5
69 7 1
69 85 5
70 16 6
70 34 6
70 61 8
70 84 1
70 93 5
71 13 3
71 15 2
71 67 9
71 83 10
71 100 5
72 61 5
73 6 2
73 64 1
74 16 5
74 69 5
76 14 3
77 31 5
77 86 1
78 12 4
78 59 2
78 66 6
79 12 5
79 22 10
79 57 10
79 88 9
80 3 3
81 18 9
81 32 1
81 87 5
82 23 7
82 49 2
83 5 5
83 74 6
83 93 10
84 42 8
84 52 6
84 74 4
84 99 8
85 7 6
85 60 5
86 7 10
88 26 5
88 60 10
89 18 4
91 11 4
91 35 5
91 53 6
92 44 6
93 28 4
93 37 5
93 48 6
93 87 4
94 42 6
94 59 8
94 83 4
95 28 6
96 62 4
97 42 6
98 2 4
98 33 2
98 91 7
99 2 8
100 21 5
100 30 6
100 66 10
100 86 7 
10
 
输出：
10-1:13
10-2:40
10-4:44
10-5:23
10-6:26
10-7:30
10-8:29
10-9:21
10-10:0
10-11:47
10-12:23
10-13:31
10-15:36
10-16:29
10-18:36
10-19:43
10-20:34
10-21:40
10-22:31
10-23:34
10-24:27
10-25:52
10-26:21
10-28:30
10-30:42
10-31:4
10-32:28
10-33:31
10-34:42
10-35:11
10-36:33
10-37:33
10-40:19
10-41:51
10-42:29
10-43:13
10-44:27
10-45:4
10-46:25
10-47:29
10-48:34
10-49:29
10-50:33
10-51:30
10-52:10
10-53:49
10-54:30
10-55:4
10-58:39
10-59:34
10-60:26
10-61:30
10-62:25
10-63:33
10-64:25
10-65:22
10-66:23
10-67:43
10-68:45
10-69:29
10-70:36
10-71:34
10-72:51
10-73:24
10-74:24
10-81:27
10-82:27
10-83:18
10-84:37
10-85:34
10-86:43
10-87:32
10-88:16
10-89:37
10-91:43
10-93:28
10-94:26
10-95:45
10-96:21
10-97:23
10-98:36
10-99:35
10-100:36

五、参考文献

  1. 算法概论 作者: Sanjoy Dasgupta / Christos Papadimitriou / Umesh Vazirani 出版社: 清华大学出版社，P127-P129
  2. 算法导论 第三版，P383-P385
posted @   CoolGin  阅读(1536)  评论(0)  编辑  收藏  举报
编辑推荐：
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列：如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列（二）：开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
阅读排行：
· Manus重磅发布：全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后，我竟然真的恢复了删除的微信聊天记录！
· 没有Manus邀请码？试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
点击右上角即可分享
微信分享提示