常见算法：二分法实现
欢迎关注公众号：李永平的个人公众号
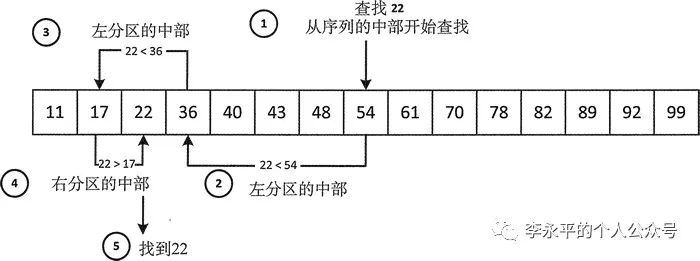
二分搜索(折半搜索)是一种在有序数组中查找某一特定元素的搜索算法。
问题描述：
在一个有序数组中，输入一个数，判断该数组中是否存在这个数。
问题分析：
已知数组为有序数组，在有序数组在查找某个数是否存在，可以折半查找。
即定义数组左边界和右边界，求出该数组的中间数，和目标数比较，若中间数大于目标数，则说明目标数在该数组的前半段，右边界为中间数减一，如果中间数小于目标数，则说明目标数在数组的后半段，左边界为中间数加一。
继续执行上述步骤，直到找到该数或者不存在。
循环的终止条件是：数组左边界大于右边界或者找到该数并返回。
有两种解决方法，递归或者非递归来实现
时间复杂度
采用的是分治策略，最坏的情况下两种方式时间复杂度一样：O(log2 N)，最好情况下为O（1）。
空间复杂度
算法的空间复杂度并不是计算实际占用的空间，而是计算整个算法的辅助空间单元的个数。
非递归方式：由于辅助空间是常数级别的所以，空间复杂度是O(1);
递归方式：递归的次数和深度都是log2 N,每次所需要的辅助空间都是常数级别的：空间复杂度：O(log2N )。
解决思路：
有两种解决方法，递归和非递归来实现二分查找，实现代码如下：
package Algorithm;
/*
* @project project
* @author liyongping
* @creed: just do it
* @ date 2022/7/6 17:42
* @ version 1.0
*/
/**
* 二分查找算法简介
*/
public class binarySearch {
public static void main(String[] args) {
binarySearch binarySearch = new binarySearch();
int[] arr = {1, 2, 3, 4, 5, 6,7};
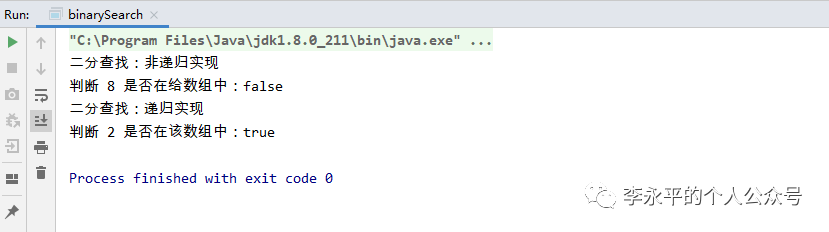
System.out.println("二分查找：非递归实现");
System.out.println("判断 8 是否在给数组中："+binarySearch.binarySearchNoRecur(arr, 8));
System.out.println("二分查找：递归实现");
System.out.println("判断 2 是否在该数组中："+binarySearch.binarySearchWithRecur(arr, 2, 0, arr.length - 1));
}
/**
* 使用非递归的方法进行二分查找
*
* @param arr 数组
* @param target 目标数
* @return
*/
public boolean binarySearchNoRecur(int[] arr, int target) {
int head = 0, tail = arr.length - 1;
while (head <= tail) {
int mid = head + (tail - head) / 2;
if (arr[mid] == target) {//如果目标数等于中间数
return true;
} else if (arr[mid] > target) {//如果中间数大于目标数
tail = mid - 1;//刷新右节点
} else {
head = mid + 1;//否则刷新左节点
}
}
return false;
}
/**
*
* @param arr 有序数组
* @param target 目标数
* @param left 左节点
* @param right 右节点
* @return
*/
public boolean binarySearchWithRecur(int[] arr, int target, int left, int right) {
if (left > right) {//先判断左右节点之间的关系
return false;
}
int mid = left + (right - left) / 2;
if (arr[mid] > target) {
return binarySearchWithRecur(arr, target, left, mid - 1);
}else if (arr[mid] < target) {
return binarySearchWithRecur(arr, target, mid + 1, right);
}else{
return arr[mid]==target ;
}
}
}
上述代码的执行结果为：
二分法常见面试题分析：
剑指OFFER 11
题目分析：
在一个旋转数组中找出最小值，可以使用暴力解法，遍历数组，找出最小值，可以使用二分法，求出最小值。
将旋转数组对半分可以得到一个包含最小元素的新旋转数组，以及一个非递减排序的数组。新的旋转数组的长度是原数组的一半，从而将问题规模减少了一半，这种折半性质的算法的时间复杂度为 O(log2N)。
算法流程：
初始化：声明 l, h 双指针分别指向 array 数组左右两端， m 代表 mid， 代表数组的中间值，m=l+(h-l)/2;
当 nums[m] <= nums[h] 时，表示 [m, h] 区间内的数组是非递减数组，[l, m] 区间内的数组是旋转数组，此时令 h = m；
否则 [m + 1, h] 区间内的数组是旋转数组，令 l = m + 1。
该解法的关键在于：
确定对半分得到的两个数组哪一个是旋转数组，哪一个是非递减数组。我们知道非递减数组的第一个元素一定小于等于最后一个元素。
package JavaOffer;/*
* @project project
* @author liyongping
* @creed: just do it
* @ date 2022/4/25 12:05
* @ version 1.0
*/
/**
*有一个长度为 n 的非降序数组，比如[1,2,3,4,5]，将它进行旋转，
* 即把一个数组最开始的若干个元素搬到数组的末尾，
* 变成一个旋转数组，比如变成了[3,4,5,1,2]，或者[4,5,1,2,3]这样的。
* 请问，给定这样一个旋转数组，求数组中的最小值。
*/
public class JZ11 {
public static void main(String[] args) {
int[] a = {4,5,6,7,1,2,3};
JZ11 jz11 = new JZ11();
int getMin = jz11.MinInArray(a);
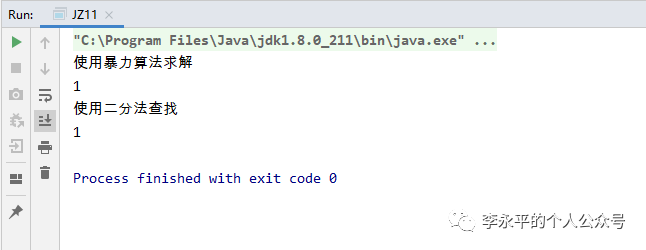
System.out.println("使用暴力算法求解");
System.out.println(getMin);
System.out.println("使用二分法查找");
System.out.println(jz11.minNumberInRotateArray(a));
}
//使用暴力算法求解
public int MinInArray(int[] array) {
int minNum = array[0];
for (int i = 1; i < array.length; i++) {
if (minNum > array[i]) {
minNum = array[i];
}
}
return minNum;
}
//使用二分法求解
//方法的本质在于使用二分法找出数组中的旋转部分，不断迭代，直到找到最小值。
public int minNumberInRotateArray(int[] nums) {
if(nums.length==0){
return 0;
}
int l=0,h=nums.length-1;
while (l<h){
int m=l+(h-l)/2; //计算中间数
//当 nums[m] <= nums[h] 时，表示 [m, h] 区间内的数组是非递减数组，[l, m] 区间内的数组是旋转数组，此时令 h = m
if (nums[m]<=nums[h]){
h=m;
}else {
l=m+1;
}
}
return nums[l];
}
}
上述代码的运行结果如下，
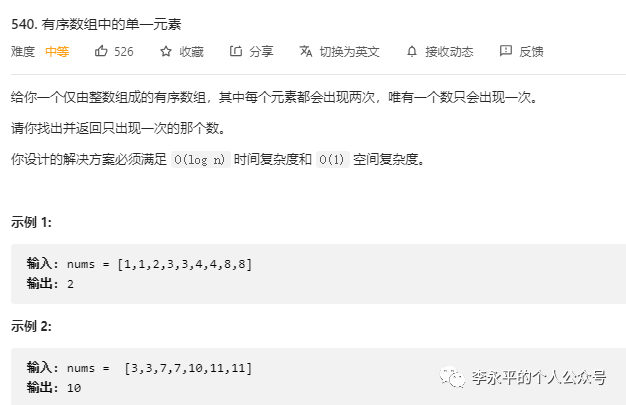
LEETCODE 540：
思路分析：
在一个有序数组中，每个元素均出现两次，有一个元素出现一次，我们要找到这个元素，有三种解法
（1）暴力解法，遍历数组，并用字典记录每个数出现几次，然后遍历字典，找出出现一次的那个数。
（2）每两个数遍历：以步长为2进行遍历，找到不符合的第一个数即为答案
（3）二分法查找：
二分查找的本质在于找到中间数，如果中间数为偶数，则判断中间数和下一个数是否相等，如果是奇数，则判断中间数和前一个数是否相等，
实现代码如下:
package JavaLeetCode;/*
* @project project
* @author liyongping
* @creed: just do it
* @ date 2022/6/11 18:15
* @ version 1.0
*/
/**
* 给你一个仅由整数组成的有序数组，其中每个元素都会出现两次，
* 唯有一个数只会出现一次。
* 请你找出并返回只出现一次的那个数。
*/
import java.util.HashMap;
import java.util.Map;
public class ld540 {
public static void main(String[] args) {
int arr[]={1,1,2,3,3,4,4,8,8};
ld540 ld540 = new ld540();
System.out.println("暴力解法查找");
System.out.println(ld540.oneNum(arr));
System.out.println("每两个遍历");
System.out.println(ld540.singleNum(arr));
System.out.println("二分法查找");
System.out.println(ld540.singleNonDuplicate(arr));
}
//暴力解法
public int oneNum(int [] arr){
int res=-1;
Map<Integer,Integer> map =new HashMap<Integer,Integer>();
for (int i = 0; i <arr.length ; i++) {
if (map.containsKey(arr[i])){
map.put(arr[i],map.get(arr[i])+1);
}else {
map.put(arr[i],1);
}
}
for(Integer integer:map.keySet()){
if (map.get(integer)==1){
res=integer;
}
}
return res;
}
//遍历
public int singleNum(int[] nums){
int res=-1;
for (int i = 0; i <nums.length-1 ; i=i+2) {
if (nums[i]!=nums[i+1]) {
res = nums[i];
break;
}
}
return res;
}
//二分法
public int singleNonDuplicate(int[] nums) {
int low = 0, high = nums.length - 1;
int tmp=0;
while (low < high) {
int mid = (high - low) / 2 + low;
if (mid%2==1){//判断当前数是奇数还是偶数
tmp=mid-1;
}else {
tmp=mid+1;
}
if (nums[mid] == nums[tmp]) {
low = mid + 1;
} else {
high = mid;
}
}
return nums[low];
}
}
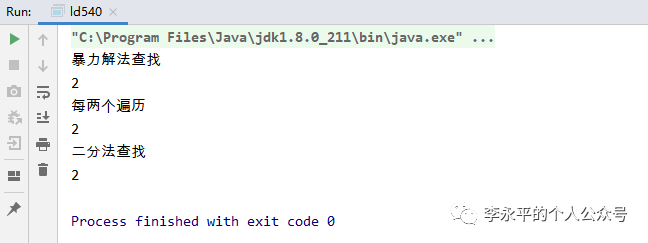
上述代码运行结果为：
