文献解读:采用波浪前缘的风电机组翼型后缘降噪实验研究
题目:采用波浪前缘的风电机组翼型后缘降噪实验研究
关键词:风能;风力发电机;噪音控制;波浪前缘;尾缘噪声
1 中文摘要
旋转叶片产生的气动噪声是制约现代风力机快速发展的重要因素。在各种噪声源中,翼型尾缘噪声对风力机噪声的贡献最大。
本文在半消声室内进行了仿生正弦波形前缘控制风力机翼型尾缘自噪声的实验研究。噪声辐射的基线NACA 0012翼型和各种波浪形翼型测量使用一个平面麦克风阵列组成的52个麦克风。采用CLEAN-SC方法实现了噪声源的识别。详细分析了速度和迎角对基线翼型噪声辐射的影响。探讨了波浪振幅和波长对翼型尾缘噪声的控制规律。基于声波束形成结果,直观地展示了波浪前缘的噪声控制效果。
一般来说,波浪形前缘振幅越大、波长越小,对翼型后缘降噪效果越好。最大声压级降低可达33.9dB。研究结果有望为风力机气动噪声控制提供重要信息。
2 关键信息提取
2.1 引言
与航空噪声类似,风电机组叶片产生的噪声会对当地居民的身心健康以及鸟类迁徙活动或动物繁殖活动产生一定的影响。随着风力发电机组的快速发展和应用,单机容量越来越大,风电机组的尺寸也越来越大。随着风轮直径和叶尖转速的增大,风电机组在工作过程中产生的噪声污染问题日益严重。
边界层湍流与翼型尾缘相互作用产生的翼型尾缘噪声是风电机组的主要噪声源。Brooks等人根据翼型附面层不同的流态,将翼型自噪声的产生机理分为五种类型。由于风力机噪声的广泛性,其噪声控制是一项具有挑战性的任务。大功率、低噪声污染是未来风力发电机组的发展方向。为了使风力发电真正实现清洁,迫切需要对风力发电机组进行系统的研究,开发先进的风力发电机组噪声控制方法。
Lutz等人提出了一种预测翼型尾缘噪声的方法,并将其应用于声学翼型设计中。他们为三台MW级参考风电机组的叶片外部区域开发了三种不同的翼型,可以在不损失性能的情况下将整体声压级降低1-3.5dB[12]。
Sanghyeon等人利用混合计算气动声学方法研究了Savonius风力机的气动噪声特性,并在了解噪声产生机理的基础上提出了低噪声设计方案。研究发现,采用s型后缘叶片可使Savonius风机的噪声水平降低2.7dB[13]。
Avallone等人对NACA 0018翼型尾缘进行了改进,以降低湍流边界层引起的尾缘噪声。通过计算和实验验证,在低到中频范围内,梳状锯齿锯齿比传统锯齿具有更好的降噪效果[14]。
一般来说,使用后缘锯齿总是导致空气动力学性能降低。为了解决这个问题,赵等人开发了一种新型的锯齿翼型,可以保持较高的气动性能[15]。
Showkat等人研究了多孔处理作为空气动力降噪的手段之一。研究了流动与多孔材料相互作用的影响,探讨了多孔材料的降噪机理[16]。
2010年,Hansen等人[18]首次研究了波浪前缘对NACA 0012翼型音调噪声的控制效果。研究发现,波浪前缘可以显著降低NACA 0012翼型在约12万雷诺数时的音调噪声。Hansen还指出,波浪状前缘的降噪机制是由结核引起的流向涡的形成,它可以增强下游边界层的动量交换,提高边界层的稳定性,破坏声波反馈机制。Gruber[19]等人研究了串联翼型使用两种类型的锯齿尾缘为上游翼型和波浪前缘为下游翼型。他们研究了波浪前缘对尾迹-翼型干扰噪声的影响,达到了5-8.5 dB的宽带干扰噪声降低。
Feinerman等[20]研究了正弦波形前缘对直升机叶片涡干涉噪声的影响。实验结果表明,波浪形前缘可降低干扰噪声达3dB,并提出其降噪机制在于相消干涉。
Chen等[21]对波浪前缘对NACA 0012翼型干涉噪声的影响进行了实验研究,并参数化了波浪前缘的幅度和波长特性。研究发现,降噪效果对波浪形前缘的振幅和波长很敏感。具有最大振幅和最小波长的波浪形前缘可以达到最显著的降噪效果,降噪效果可达4dB。
大多数研究采用尾缘锯齿形来控制翼型尾缘噪声[22],而由座头鲸鳍形启发的波浪前缘常用于控制翼型前缘湍流相互作用噪声[23-25]。然而,很少有研究解决了波浪形前缘对翼型后缘噪声[26]的影响。
Lacagnina等[27]研究了前缘锯齿在大迎角范围内降低翼型自噪声的效果。结果表明,在大多数迎角下,前缘锯齿可以降低翼型的自噪声,但对气动性能有负面影响。Kim等[28]也研究了NACA 65(12)-10翼型与正弦前缘波动。在有效雷诺数为106的条件下,考虑附着流和分离流对翼型气动性能和声学性能进行了优化。最大升力的翼型是没有牺牲整体噪音和阻力在近/后失速攻角改进。同时考虑气动性能和噪声水平,提出了一种最优的前缘波动结构。
本研究的目的是利用波浪前缘降低小迎角和大航速范围下的翼型尾缘噪声,并探索不同振幅和波长的波浪前缘的降噪规律。
【参考文献】
[12] Lutz, T.; Herrig, A.; Würz, W.; Kamruzzaman, M.; Krämer, E. Design and wind-tunnel verification of low-noise airfoils for wind turbines. AIAA J. 2007, 45, 779–785.
[13] Sanghyeon, K.; Cheolung, C. Development of low-noise drag-type vertical wind turbines. Renew. Energy 2015, 79, 199–208.
[14] Avallone, F.; Van Der Velden, W.C.P.; Ragni, D.; Casalino, D. Noise reduction mechanisms of sawtooth and combed-sawtooth trailing-edge serrations. J. Fluid Mech. 2018, 848, 560–591.
[15] Zhao, M.; Cao, H.; Zhang, M.; Liao, C.; Zhou, T. Optimal design of aeroacoustic airfoils with owl-inspired trailing-edge serrations.Bioinspir. Biomim. 2021, 16, 056004.
[16] Showkat, A.S.A.; Azarpeyvand, M.; Ilário, D.S.C.R. Trailing-edge flow and noise control using porous treatments. J. Fluid Mech.2018, 850, 83–119.
[17] Fish, F.E.; Battle, J.M. Hydrodynamic design of the Humpback Whale Flipper. J. Morphol. 1995, 225, 51–60.
[18] Hansen, K.L.; Kelso, R.M.; Doolan, C.J. Reduction of flow induced tonal noise through leading edge tubercle modifications. In Proceedings of the 16th AIAA/CEAS Aeroacoustics Conference, Stockholm, Sweeden, 7–9 June 2010; p. 3700.
[19] Gruber, M.; Joseph, P.F.; Polacsek, C.; Chong, T.P. Noise reduction using combined trailing edge and leading edge serrations in a tandem airfoil experiment. In Proceedings of the 18th AIAA/CEAS Aeroacoustics Conference (33rd AIAA Aeroacoustics Conference), Colorado Springs, CO, USA, 4–6 June 2012; p. 2134.
[20] Feinerman, J.A.; Koushik, S.; Schmitz, F.H. Effect of leading-edge serrations on helicopter blade-vortex interaction noise. J. Am.Helicopter Soc. 2017, 62, 1–11.
[21] Chen, W.J.; Qiao, W.Y.; Tong, F. Experimental investigation of wavy leading edges on rod-aerofoil interaction noise. J. Sound Vib.2018, 422, 409–431.
[22] Stahl, K.; Manegar, F.; Carouls, T.; Binois, R. Experimental investigation of self-aligning trailing edge serrations for airfoil noise reduction. In Proceedings of the 8th International Conference on Wind Turbine Noise, Lisbon, Portugal, 12–14 June 2019.
[23] Chaitanya, P.; Joseph, P.; Narayanan, S. Performance and mechanism of sinusoidal leading edge serrations for the reduction of turbulenc-aerofoil interaction noise. J. Fluid Mech. 2017, 818, 435–464.
[24] Aguilera, F.G.; Gill, J.; Angland, D. Wavy leading edge airfoils interacting with anisotropic turbulence. In Proceedings of the 23rd AIAA/CEAS Aeroacoustics Conference, Denver, CO, USA, 5–9 June 2017; p. 3370.
[25] Chen, W.J.; Qiao, W.Y.; Tong, F.; Wang, L.F.; Wang, X.N. Numerical investigation of wavy leading edges on rod-airfoil interaction noise. AIAA J. 2018, 56, 2553–2567.
[26] Chen, W.; Qiao, W.; Duan, W.; Wei, Z. Experimental study of airfoil instability noise with wavy leading edges. Appl. Acoust. 2021,172, 107671.
[27] Lacagnina, G.; Chaitanya, P.; Kim, J.H.; Berk, T.; Joseph, P.; Choi, K.S.; Ganapathisubramani, B.; Hasheminejad, S.M.; Chong, T.P.;Stalnov, O.; et al. Leading edge serrations for the reduction of aerofoil self-noise at low angle of attack, pre-stall and post-stall conditions. Int. J. Aeroacoust. 2021, 20, 130–156.
[28] Kim, J.H.; Choi, K.S.; Lacagnina, G.; Chaitanya, P.; Joseph, P.; Hasheminejad, S.M.; Pei Chong, T.; Shahab, M.F.; Omidyeganeh, M.;Pinelli, A. Aerodynamic and aeroacoustic optimization of leading-edge undulation of a naca 65 (12)-10 airfoil. AIAA J. 2022, 60,2342–2353.
2.2 实验过程
2.2.1 波浪前缘设计
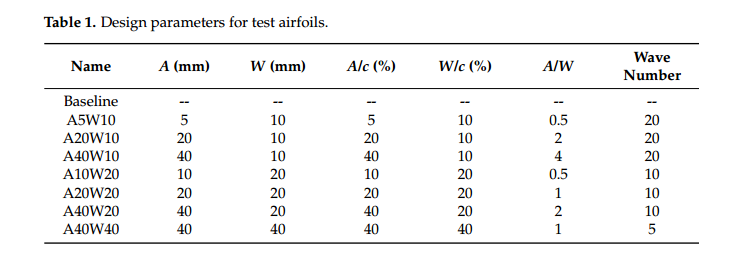
在这项研究中,NACA 0012翼型与弦长100mm和225mm的跨度长度被用作基线翼型。研究了7种不同幅值(A)和波长(W)的正弦波型前缘翼型。详细设计参数如表1所示。
所有波浪翼型的标志是基于弦长振幅和波长的无因次百分比的组合。如图1b所示,局部弦长仅通过拉伸和压缩从前缘到最大厚度位置的几何形状来改变,保持波浪形前缘翼型的平均弦长和投影面积与基线翼型一致。波浪型前缘翼型弦长沿展向的变化由式(1)定义,展跨截面由式(2)生成。
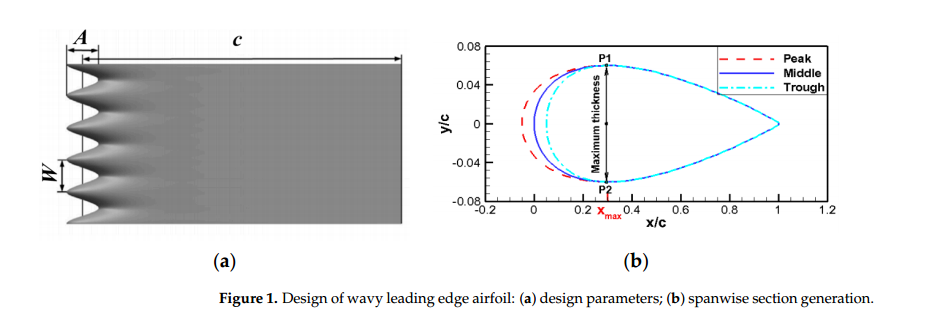
下标“新”代表波浪形前缘翼型和“旧”代表基线翼型。Xmax表示基线翼型的最大厚度位置。
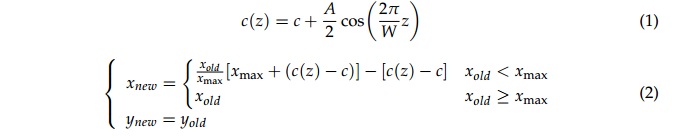
本文研究的8个翼型均采用计算机数控(CNC)机床加工的铝材制成,实物如图2所示。为了确保跨向方向包括波长的整数倍,并便于可拆卸的安装,12.5mm被保留在翼型的两端,这意味着实际跨度长度包括波浪形前缘是200mm。

2.2.2 测试设备和仪器
本研究在西北工业大学涡轮机械空气动力学与气动声学实验室(TAAL)的半消声室进行,如图3所示。风洞出口尺寸为225 × 120 mm,最大来流速度为100 m/s,湍流强度约为1%。试验翼型由两个平行的有机玻璃板安装在距离喷管出口50毫米的距离,如图4所示。
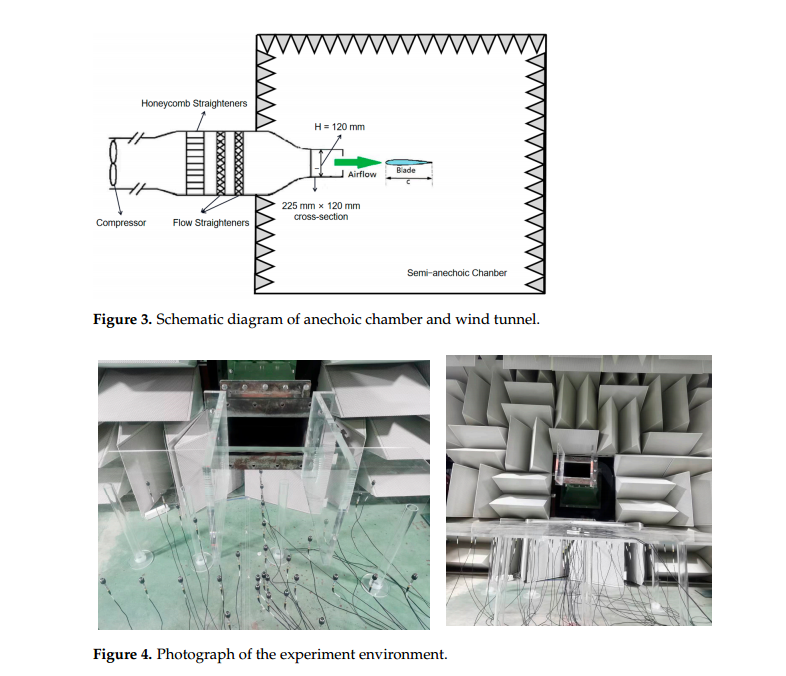
根据现代风电机组的尺寸和基本转速,选择了20 ~ 70 m/s的实验来流速度范围,间隔为10 m/s。可变几何攻角范围设为±15°,间隔为5°。
由于翼型安装在一个开放的喷气风洞中,它可以引起来流的下洗,导致有效攻角的减少。Brooks等人在等升力面理论的基础上,提出了二维开喷风洞的修正公式。修正后的迎角相当于在自由流动条件下产生的相同升力所对应的迎角。
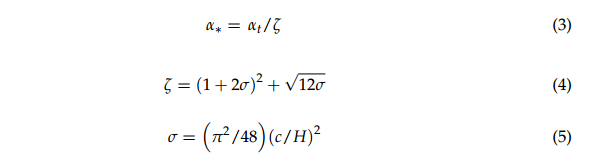
其中at为几何迎角,a*为有效迎角,c为翼型弦长,对于水平安装的翼型,H为风洞出口高度。在本研究中,H = 120 mm。使用上述公式修正攻角,修正后的实际有效攻角范围计算为±5◦。10◦的几何攻角对应于3.4°的有效攻角。
如图4所示,一个由52个BSWA MPA401 1/4英寸麦克风组成的螺旋平面麦克风阵列被放置在距离翼型后缘450 mm的地方,使用CLEAN-SC方法识别声源。1#麦克风(在麦克风阵列面板的中心)直接位于翼型后缘的中点以下。麦克风阵列面板的几何模型和实际照片如图5所示。

声压级(SPL)由式(6)定义,其中Spp为声压的功率谱密度,Pref为参考声压。本实验的采样频率为32,768 Hz,每组声信号的采样时间为20 s。采用Welch的方法计算声压功率谱密度。傅里叶变换点个数为1024,数据重叠率为50%,窗函数为Hamming窗。光谱分辨率为32hz,平均次数为1279次。
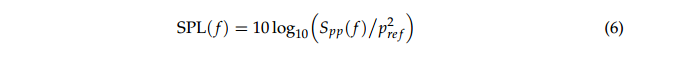
2.3 结果与讨论
2.3.1 基线气流的噪声辐射
(Noise Radiations of the Baseline Airfoil)
首先,研究了来流速度和迎角对基线翼型噪声辐射的影响。如图6所示,噪声谱的基线翼型测量的麦克风#1在不同的速度在0◦和10◦几何角度的攻击比较。由于背景噪声是2kHz以下的主要噪声源,本文只讨论了2kHz ~ 10 kHz范围内的噪声辐射特性。从图中可以看出,翼型辐射的宽带噪声一般随着来流速度的增大而增大。同时,如图6b所示,噪声峰的频率也随着来流速度的增加而逐渐增加,并且随着流速的增加,噪声峰会先增大后减小。图6a还显示了不同速度下背景噪声(BGN)的频谱。实线代表的情况下,有一个基线翼型没有攻角,而虚线代表的情况下,没有翼型,只有风洞和亚克力板用于固定翼型。可以看出,宽带噪声水平的背景是普遍低于当有一个基线翼型。然而,背景噪音可以更高,接近5200赫兹,这可能是由于在丙烯酸板的尾缘涡脱落的影响翼型。
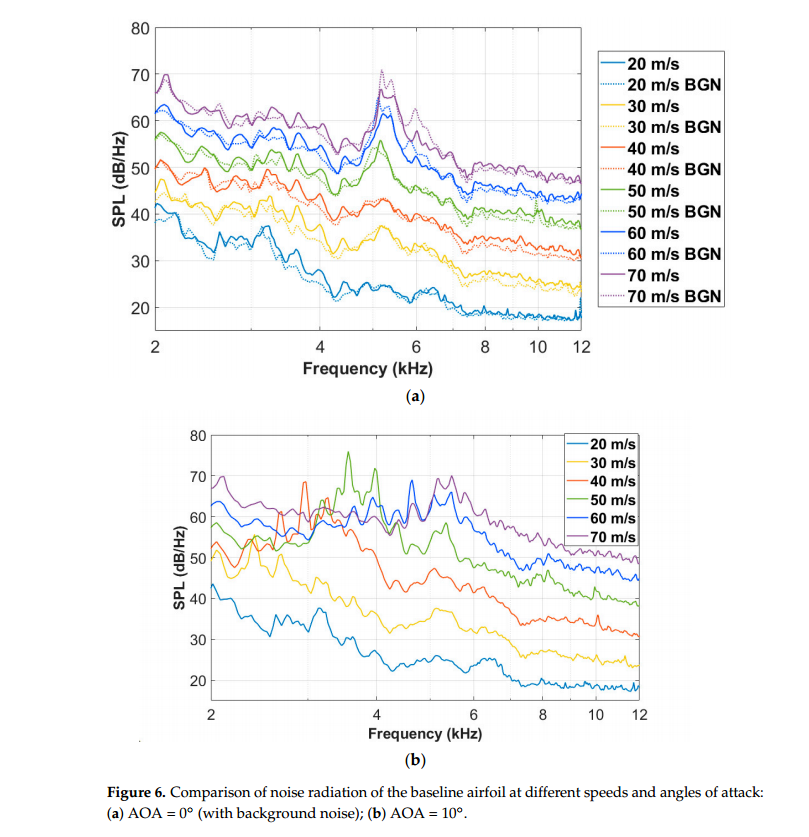
图7显示了当来流速度为40、50和60 m/s时,基线翼型在不同几何迎角下的噪声辐射对比。从不同速度下的图像可以得到噪声辐射水平随攻角的增大而增大的规律。区别在于驼峰噪声的频率范围,如前所述,它随速度变化。由图7b可以看出,当来流速度为50 m/s时,2600 ~ 4500hz驼峰噪声声压级和6000 ~ 9000 Hz宽带噪声声压级都随着迎角的增大而增大。需要注意的是,5200赫兹附近的噪声峰实际上是由用于固定翼型的有机玻璃板引起的背景噪声,这里不考虑。在2600 - 4500hz的频率范围内,基线翼型的驼峰噪声从0◦迎角时的53 dB增加到5◦迎角时的59 dB,而在10◦迎角时,最大声压级可达76dB。
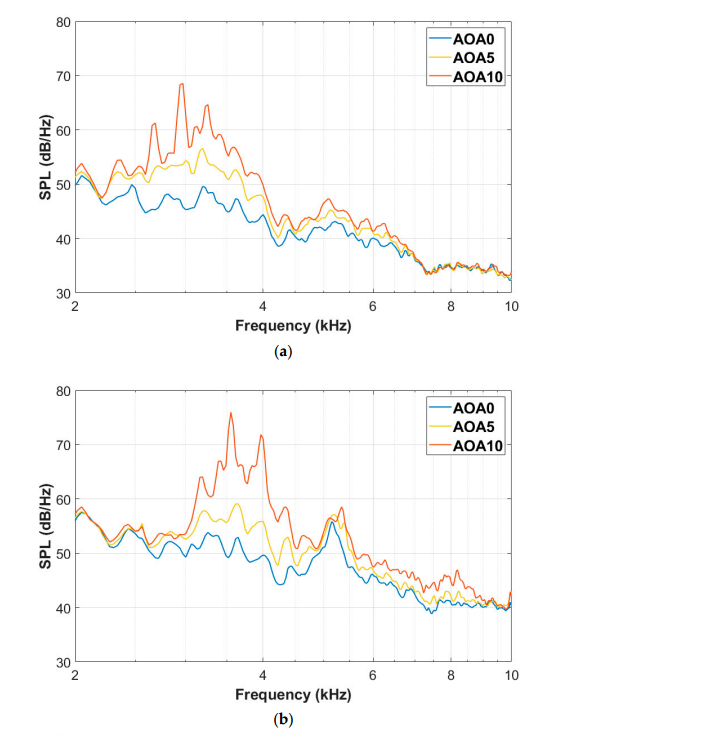
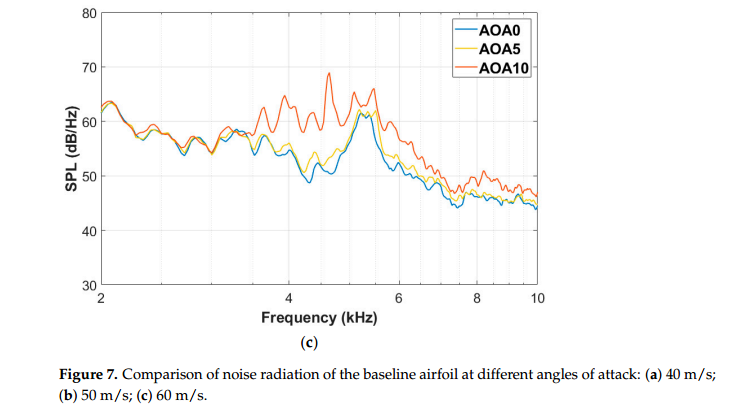
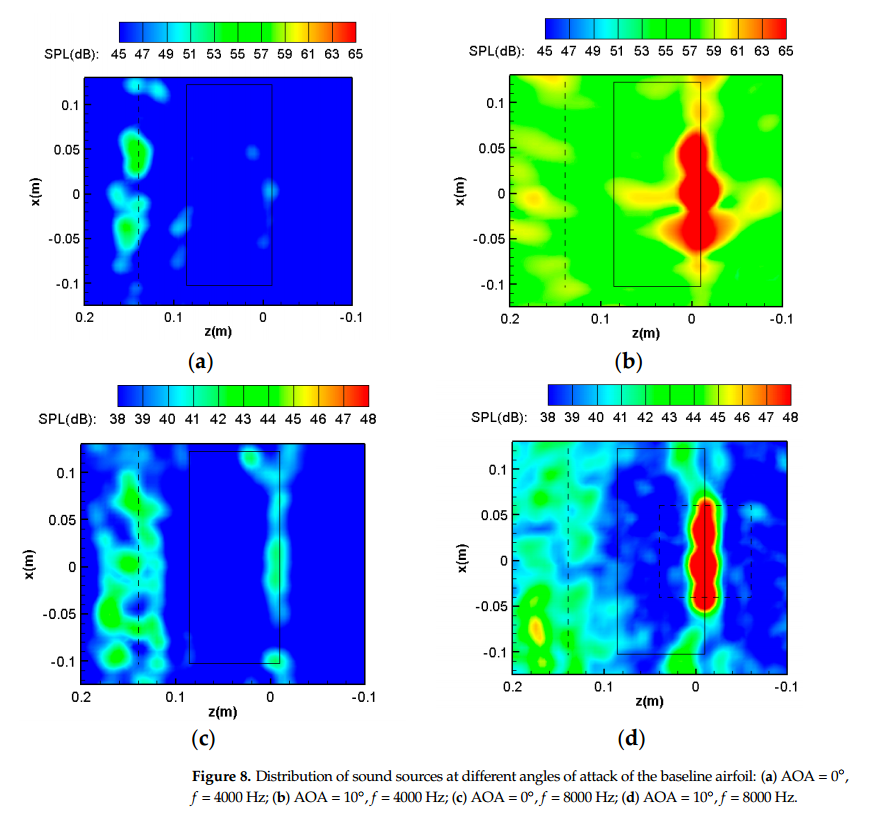
图8为来流速度为50 m/s,迎角分别为0◦和10◦时,基线翼型在不同三分之一倍频中心频率下的声源识别结果。图中的虚线和实框分别表示风洞出口和翼型的相对位置。从图中可以看出,当迎角从0◦到10◦变化时,导致4 kHz和8 kHz噪声增加的主要声源都在翼型后缘。为了尽量减少背景噪声的影响,将图8d中虚线方框区域内的噪声谱取平均值,得到后缘噪声,用于后续分析。
2.3.2 波浪翼型的降噪效果
图9显示了基线翼型、A10W20翼型和A40W20翼型在来流速度为50 m/s、攻角为10◦时的声源识别结果。同一频率下声压级轮廓线的显示范围相同。可以观察到,对于所有的翼型,噪声集中在中间翼型后缘。波浪形前缘可以有效地控制翼型后缘噪声,振幅较大的A40W20翼型对翼型尾缘噪声的降噪效果明显优于A10W20翼型。

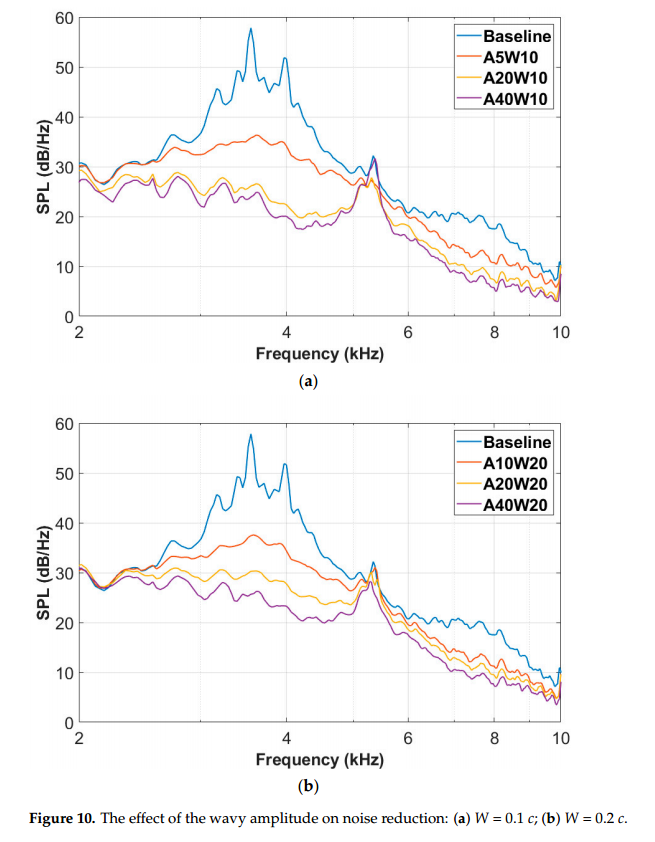
波浪形前缘幅值对后缘噪声声压级谱的影响如图10所示。来流速度为50m/s,几何迎角为10◦。可以得出,当波浪形前缘的波长保持一致时,振幅越大,降噪效果越好。图10a、b对于不同波长具有相同的降噪规律。我们还可以看到,当波浪形前缘的幅波长比(A/W)相同时,如A5W10与A10W20或A20W10与A40W20,波浪形翼型的噪声谱相似,降噪水平也具有可比性。然而,在图10a中,当波浪形前缘的A/W比增加到4时,与A20W10波浪形翼型相比,A40W10波浪形翼型的降噪效益相对较小。
波浪形前缘波长对后缘噪声辐射的影响如图11所示。从图11a可以观察到,当振幅为0.2c时,A20W10翼型的降噪效果优于A20W20翼型。同样,在图11b中,当振幅保持在0.4c时,随着波长的增加,降噪效果越来越差。此外,A40W40翼型导致声压级在2000和2500赫兹之间的增加。

研究结果表明:
本文所研究的所有波浪前缘都具有降低翼型后缘噪声的作用,包括驼峰噪声和宽带噪声。此外,波幅较大、波长较小的波形前缘能较好地控制后缘噪声。特别是,A40W10翼型被发现具有最有效的降噪能力。结果表明,在2500 ~ 5000Hz的迎角范围内,A40W10翼型完全抑制了尾缘驼峰噪声,在3552 Hz时最大降噪水平为33.9 dB。此外,5600-10,000Hz之间的宽带噪声也得到了有效降低,在7500Hz左右的最大降噪水平为12.7dB。其次,波浪形翼型A40W20和A20W10在降噪方面也很有效,在3552Hz时最大声压级分别降低32.1dB和31.7 dB。
本研究存在一定的局限性:
(1)本研究使用的研究对象为二维对称翼型,对实际叶片进行了简化,没有考虑其三维特性。然而,实际风力机在不同半径位置的叶片形状和扭转角是不同的。
(2)本研究模拟通过改变迎角和来流速度,得到不同叶片半径处的实际情况。然而,本研究的攻角和速度范围有限,只研究了小攻角下20-70 m/s的速度范围。事实上,波浪型前缘对大迎角下的流动分离也有一定的控制作用,可以有效降低翼型的分离噪声。
(3)本研究是在半消声室内进行的,因此背景噪声的影响比较显著。2000Hz以下的低频噪声和5200Hz附近的驼峰噪声主要由背景噪声主导,在某些来流条件下,背景噪声可能掩盖翼型噪声。
3 结论
本文实验研究了基线NACA 0012翼型和7种不同振幅和波长的波浪型前缘翼型在20 ~ 70 m/s 7种速度和0 ~ 15◦4个攻角下的噪声辐射特性。分析了波形边缘的振幅和波长对降噪效果的影响。通过波束成形声源识别技术,直观地呈现出声源的分布和波浪形前缘结构的降噪效果。根据实验结果,得出以下结论:
(1)基线翼型辐射的宽带噪声一般随来流速度的增加而增加。同时,由于迎角的存在,会产生驼峰噪声,增加宽带噪声。噪声峰的频率随来流速度的增加而逐渐增大,噪声峰的频率随来流速度的增加先增大后减小。在小迎角范围内,基线翼型的声压级随着迎角的增大而增大,主要噪声源位于翼型后缘。在10◦攻角和50 m/s下,3552 Hz时的最大声压级可达76 dB,与0◦攻角时的53 dB相比增加了23 dB。
(2)波浪形前缘能有效控制翼型尾缘噪声,波浪形前缘振幅较大、波长较小能达到较好的降噪效果。例如,当来流速度为50 m/s时,波浪形前缘有效抑制了2500-5000 Hz范围内的驼峰噪声,同时也有效降低了5600 Hz以上的宽带噪声。在研究的翼型中,A40W10翼型表现出最有效的降噪效果,最大降噪幅度高达33.9 dB,从基线翼型的57.8 dB降至A40W10翼型的23.9 dB。

 在半消声室内进行了仿生正弦波形前缘控制风力机翼型尾缘自噪声的实验研究,基于声波束形成结果,展示了波浪前缘的噪声控制效果,波浪形前缘振幅越大、波长越小,对翼型后缘降噪效果越好。最大声压级降低可达33.9dB。
在半消声室内进行了仿生正弦波形前缘控制风力机翼型尾缘自噪声的实验研究,基于声波束形成结果,展示了波浪前缘的噪声控制效果,波浪形前缘振幅越大、波长越小,对翼型后缘降噪效果越好。最大声压级降低可达33.9dB。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号