文献解读：基于流-固-声耦合技术对风电机组噪声预测和控制方法的研究

题目：基于流-固-声耦合技术对风电机组噪声预测和控制方法的研究
关键词：气动声学；风电机组；噪声模型；噪声控制；

1 中文摘要

  本文使用的数值工具是耦合的Navier-Stokes/致动器线模型ElliSys3D/AL，结构模型FLEX5和噪声预测模型BPM框架。模拟和测试对象是LM风电公司的NM80风电机组。首先通过风切变和偏航作用下的现场荷载实测验证了耦合规范，得到了较好的一致性。然后利用耦合程序对风切变和偏航作用下的风电机组噪声源控制进行了研究。
  结果表明，在切变指数为0.3的中等风切变条件下，螺距控制策略可使平均噪声排放降低0.4 dB左右，并使主要发生在低频区的调制深度略有降低。

2 关键信息提取

2.1 引言

  与其他噪声源相比，由叶片在空气中运动引起的风电机组噪声通常被视为引起极大烦恼的重要方面。在丹麦的法规条例[2]中，现代风电机组的安装距离居民区至少应该是其顶端高度的4倍。即使隔着这么远的距离，风轮产生的声压级（SPL）仍然超过40dB(A)，几乎相当于一些普通家用电器的声压级。风力机在风切变和偏航状态下运行时，叶片载荷会产生周期性变化，从而加剧了所产生噪声的调幅，从而给附近居民带来更多的烦恼。

【参考文献】

[2]Danish Regulation for Wind Turbine Noise; Ministry of Environment and Food of Denmark: Copenhagen,Denmark, 2019. Available online:https://mst.dk/service/nyheder/nyhedsarkiv/2019/feb/ny-bekendtgoerelseom-stoej-fra-vindmoeller/ (accessed on 13 February 2020).

  风电机组或风电场的噪声在运行过程中具有不同声压幅值的调幅特征。调幅噪声有两种类型：一种是由于叶片噪声指向性改变而产生的，另一种是由非均匀入流和运行引起的，例如风切变和偏航的运行。表征调制深度的方法有三种（日本的F-S方法[5]、英国的[6]和最小-最大值方法[7]）。Barlas等[8]利用先进的计算流体力学（CFD)（EllipSys3D/AL）和基于求解抛物波方程的声音传播模型研究了风力机尾流引起的调幅，发现即使在相同噪声源强度下，调幅深度也可以达到4-5dB。

【参考文献】

[5]Fukushima, A.; Yamamoto, K.; Uchida, H.; Sueoka, S.; Kobayashi, T.; Tachibana, H. Study on the amplitude modulation of wind turbine noise: Part 1—Physical investigation. In Proceedings of the INTER-NOISE,Innsbruck, Austria, 15–18 September 2013.

[6]Coles, D.; Levet, T.; Cand, M. Application of the UK IOA Method for Rating Amplitude Modulation.In Proceedings of the 7th International Conference on Wind Turbine Noise, Rotterdam, the Netherlands,2–5 May 2017.

[7]]Fernandez, F.A.; Burdisso, R.A.; Arenas, J.P. Indoor simulation of amplitude modulated wind turbine noise.
Wind Energy 2017, 20, 507–519.

[8]Barlas, E.; Zhu, W.J.; Shen, W.Z.; Kelly, M.; Andersen, S.J. Effects of wind turbine wake on atmospheric sound propagation. Appl. Acoust. 2017, 122, 51–61.

  1985年，Grosveld[10]利用Schlinker合成的直升机噪声公式，计算了几台双叶片低功率下风水平轴风力机的发射噪声，结果与实测数据吻合较好。
  1989年，Brooks等人[13]使用风洞声学测量的国家航空咨询委员会（NACA）0012翼型提出翼型自噪声预测模型（BPM）。
  1996年Fuglsang和Madsen[14]采用BPM模型和由Amiet模型[16]修正的Lowson[15]引入的入流噪声模型计算Vestas V27型风机的噪声发射。
  2003年，国家可再生能源实验室（NREL）[17]开发了基于BPM模型的NREL翼型噪声（NAFNoise）。
  2005年，丹麦技术大学（DTU）的Zhu等人通过将真实叶片几何形状纳入预测风力涡轮机噪声产生的BPM进行了改进。
  2009年，Bowdler[19]利用在风电场现场收集的现场数据，研究了风切变在一天和一年中的不同地点和不同时间对噪声的影响。
  2015年，Oerlemans[20]研究了风切变对风力机噪声调幅的影响。
  2016年，Yuan和cott[21]利用Monin-Obukhov相似理论研究了风切变和大气湍流对风力机噪声的影响。

  为了预测尾缘噪声，Parchen[22]利用远场声压级与尾缘表面压力谱之间的关系，将远场声谱作为湍流边界层量的函数，建立了更先进的尾缘噪声模型（TNO）。Kamruzzaman等[23]人利用CFD建立了一种改进的TNO模型，考虑了尾缘边界层的非各向同性问题。Tian[24]扩展了Amiet的模型来模拟风电机组的噪声。

【参考文献】

[10]Grosveld, F.W. Prediction of Broadband Noise from Horizontal Axis Wind Turbines. J. Propuls. Power 1985,
1, 292–299.

[11]De Wolf, W.B. EEN Predictiemethode voor het Aerodynamische Geluid van Windturbines met Horizontale
AS. In NLR TR 870181L; Netherlands Aerospace Centre: Amsterdam, the Netherlands, 1986.

[12]Viterna, L.A. The NASA-LeRC Wind turbine sound prediction code. In NASA CP-2185; NASA Lewis Research Center: Cleveland, OH, USA, 1981.

[13]Brooks, T.F.; Pope, D.S.; Marcolini, M.A. Airfoil self-noise and prediction. In NASA RP-1218; NASA Langley Research Center: Hampton, VA, USA, 1989.

[14]Fuglsang, P.; Madsen, H.A. Implementation and verification of an aeroacoustic noise prediction model for wind turbines. In Risø-R-867(EN); Risø National Laboratory: Roskilde, Denmark, 1996.

[15]Lowson, M.V. Assessment and prediction of wind turbine noise. In Flow Solutions Report 92/19—ETSU
W/13/00284/REP; Harwell Laboratory, Energy Technology Support Unit: Harwell, UK, 1992.

[16]Amiet, R.K. Acoustic radiation from an airfoil in a turbulent stream. J. Sound Vibr. 1975, 41, 407–420.

[17]Moriarty, P.; Migliore, P. Semi-empirical aeroacoustic noise prediction code for wind turbines.In NREL/TP-500-34478; National Renewable Energy Lab.: Golden, CO, USA, 2003; pp. 1–39.

[18]Zhu, W.J.; Heilskov, N.; Shen, W.Z.; Sørensen, J.N. Modeling of aerodynamically generated noise from wind turbines. J. Solar Energy Eng. 2005, 127, 517–528. 

[19]Bowdler, D. Wind shear and its effect on noise assessment. In Proceedings of the Third International Conference on Wind Turbine Noise, Aalborg, Denmark, 17–19 June 2009. Available online: https://www.dickbowdler.co.uk/content/publications/Wind-Shear-and-its-Effect-on-Noise-Assessment.pdf (accessed on 26 October 2020).

[20]Oerlemans, S. Effect of wind shear on amplitude modulation of wind turbine noise. Int. J. Aeroacoust. 2015,
14, 715–728. [CrossRef]

[21]Tian, Y.; Cotté, B. Wind turbine noise modeling based on Amiet’s theory: Effects of wind shear and
atmospheric turbulence. Acta Acust. United Acust. 2016, 102, 626–639.

[22]Parchen, R. Progress report DRAW, a prediction scheme for trailing-edge noise based on detailed boundary-layer characteristics. In TNO-Report HAG-RPT-980023, Report; TNO Institute of Applied Physics:The Hague, the Netherlands, 1998.

[23]Kamruzzaman, M.; Lutz, T.; Würz, W.; Shen, W.Z.; Zhu, W.J.; Hansen, M.; Bertagnolio, F.; Madsen, H.A.Validations and improvements of aeroacoustics models using detailed experimental data. Wind Energy 2012,15, 45–61.

[24]Tian, Y. Modeling of Wind Turbine Noise Sources and Propagation in the Atmosphere. Ph.D. Thesis, ENSTA
Paris Tech, Palaiseau, France, 2016.

2.2 原理和方法

  通过Sørensen和Shen[25]引入的致动线（AL）方法对风电机组的流场进行建模，该方法在DTU内部有限体积代码EllipSys3D中实现。Kleusberg等人[26,27]成功地将执行器线法与高阶谱法相结合。EllipSys3D是由DTU[28]机械工程系和Risø国家实验室[29]风能部合作开发。AL方法[25,30]采用沿旋转线分布的体力来表示风力机叶片的气动载荷。在Navier-Stokes方程中施加的体力由DTU开发的气动弹性程序flex5[31]计算。FLEX5和EllipSys3D/AL方法的耦合在每个时间步进行。来自EllipSys3D/AL的叶片流动数据从流动网格中插值，然后输入FLEX5。
  利用以上信息，在FLEX5中计算攻角和相对速度（包括叶片变形/运动），并通过使用表示的翼型升力、阻力和力矩与攻角（AoA）数据（包括动态失速）进一步获得叶片上的气动载荷。来自FLEX5的新叶片位置和负载，包括叶片弯曲和转子运动（上/下/左右/旋转）的影响，然后作为移动执行器线上的体力输入EllipSys3D/AL。利用这些新的叶片位置，将新的载荷重新分配到CFD网格上，并在EllipSys3D/AL中得到新的求解方案。在标准气动弹性程序中，采用叶片动量理论（BEM）作为气动模型来计算这些效应和运动。
  本文采用高保真Navier-Stokes人工智能方法来解决流固耦合问题。为了进行大涡模拟，采用了TaPhuoc[32,33]的混合比例模型。为了计算叶片的噪声发射，使用BPM代码。在FLEX5中计算攻角和相对速度变量，并将其反馈给BPM。结合EllipSys3D/AL、FLEX5和BPM框架的流程图如图1所示。

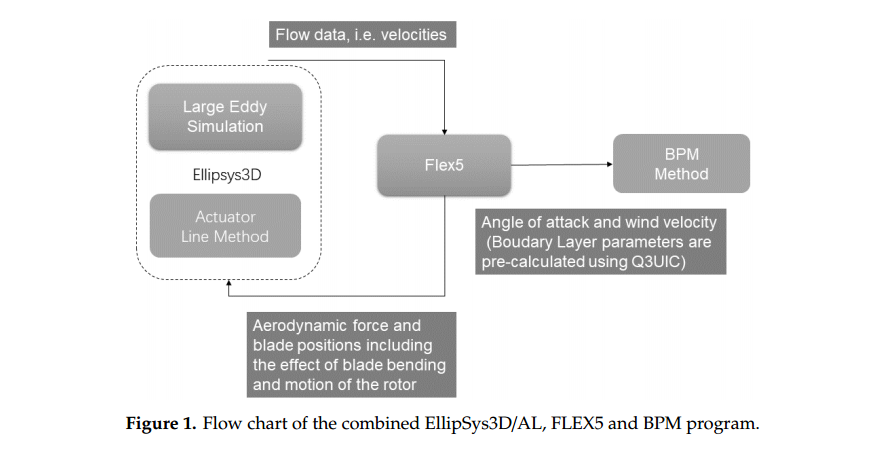
2.3 数值计算结果

2.3.1 仿真框架的验证

  此部分不做过多赘述，如有兴趣可查阅原文。关键图表如下：

2.3.2 功率和载荷仿真

  此部分不做过多赘述，如有兴趣可查阅原文。

2.3.3 声学分析

风切变和偏航对噪声排放的影响
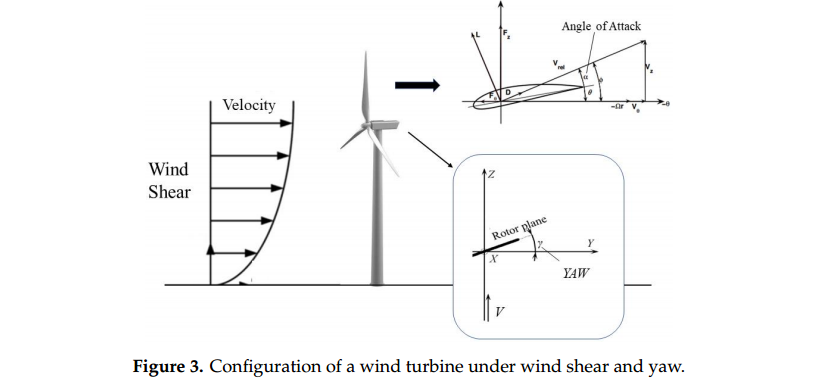
  观察者位于1.5m的高度，距离风电机组下游500m。选择500m距离的下游位置是为了尽量减少叶片噪声指向性变化产生的调幅噪声。计算中使用的声速为340m/s。湍流等级和湍流长度尺度分别设置为3%和100m。这个选择是根据场景中定义的0.3风切变指数做出的。当测量到详细的流量信息时，可以做出更现实的选择。0◦方位角是定义当叶片1垂直向下，并与塔重合。所有这四个场景都是在没有控制的情况下执行的。

  从case1和case3中可以看出，考虑剪切时，声压级略大，而在10◦偏航时，即在case2和case4中，声压级都显著降低。通常，当一个叶片指向上方时，声压级最高。从BPM声音预测方程可以看出声压级与迎面而来速度的5次幂有关。对于三片叶片的情况，在零方位角（叶片1指向向下），其他两个叶片指向120◦和240◦时，噪声在case3case4的运行过程中几乎是最高的。

  图13说明了不同控制方案下SPL的比较。可以观察到，与非控制案例相比，case1和case2的受控SPL结果，即采用控制技术I和II，是相似的。对于case1，两种控制策略的峰值是一致的，而无控制结果的幅度略小。对于case2，波动也通常是同步的，峰值的时间和幅度都是一致的。因此，控制技术的实施可能不会导致无剪切情况下的噪声降低。在case1和case2中，差异可以忽略的主要原因是桨距和相应的AoA的变化相对较小，其中噪声级的波动主要是由于叶片偏转。对于更大的投球，预计会有更大的差异。

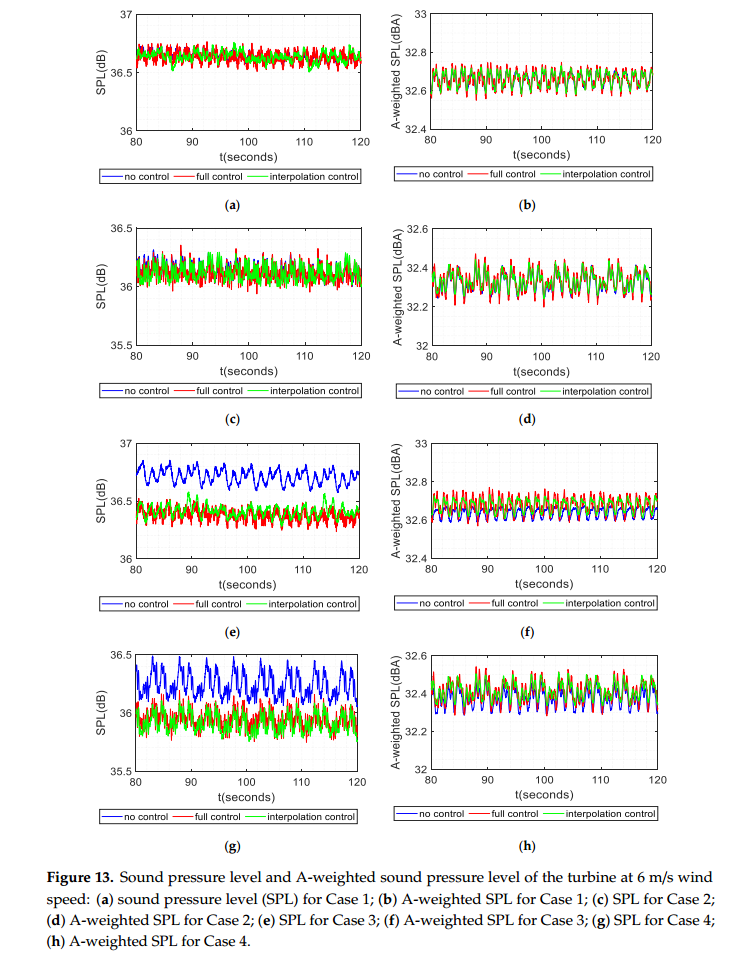
  值得注意的是，由于偏航引起的轴向风速较低，与情况1相比，情况2对应的声压级略低。对于情况3和4，通过引入控制策略I或II，可以观察到更大的声压级下降，即约0.4 dB，而趋势保持不变。
  两种控制方法的结果无显著差异。结果表明，通过引入控制技术，可以实现剪切工况下的声压强度降低。将图8中的攻角图与图13中的声压级图进行比较，可以看出由于叶片结构响应，这两个量之间存在非线性效应。图8d中插补控制的AoA变化减少了约1◦。根据1◦AoA降低1 dB降噪[39]的规律，本研究的噪声变化在此范围内。为了进行比较，可以观察到，在所有情况下，A计权SPL的控制和非控制结果之间的差异可以忽略不计。

  图14显示了在时间瞬间（120s）不同频率下声压级的贡献。从图中可以看出，在低频（小于315 Hz），通过螺距控制策略，声压级明显降低。

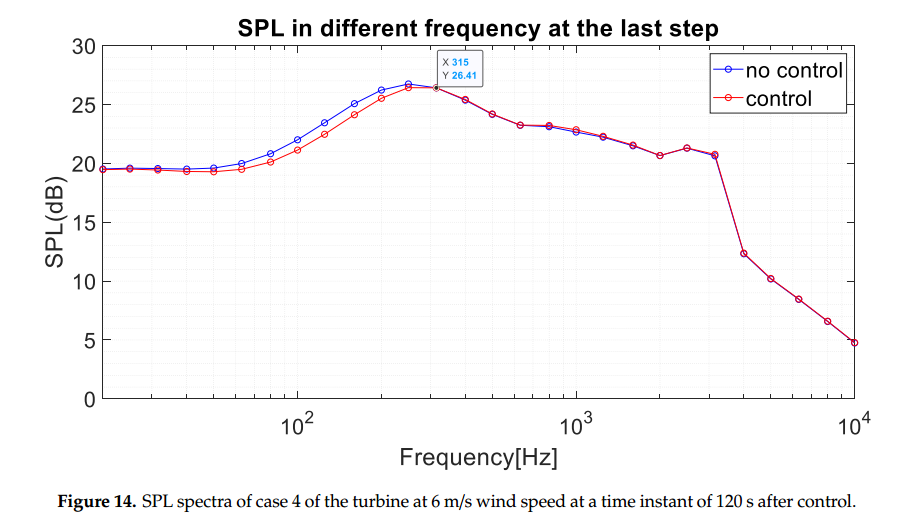
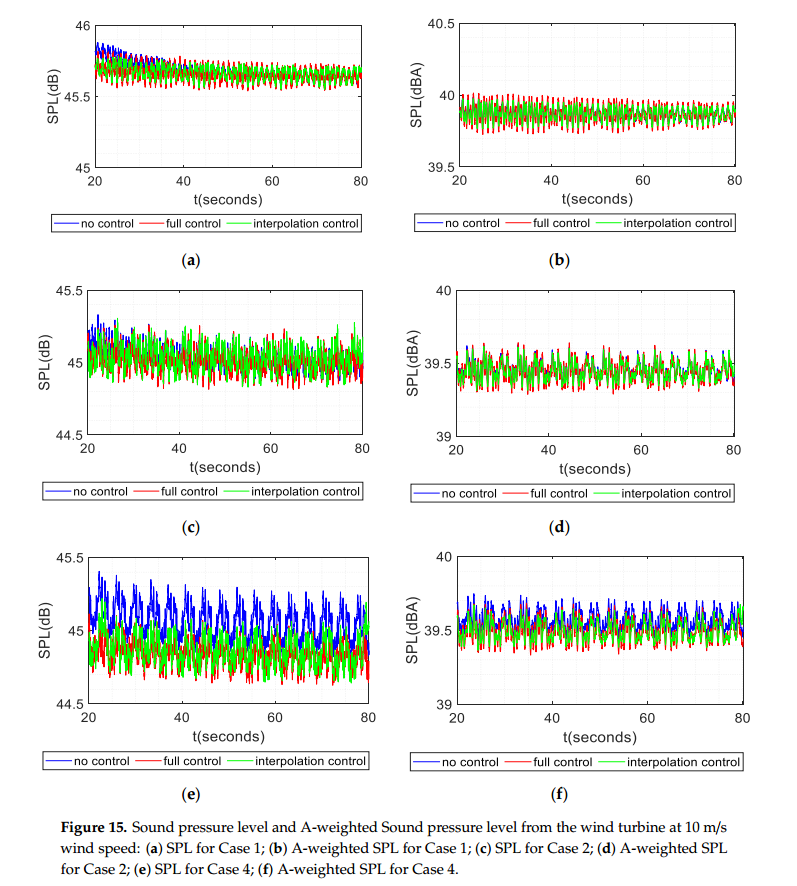
  图15显示了情况1、2和4的声压级和a加权声压级，但入流风速更大，为10 m/s。随着风速的增大，声压级均增加8.5 dB左右。值得注意的有趣的事情是，10米/秒时的音调控制方法在情况4中显示出与6米/秒时相似的效果，但振幅的变化更为重要。由于a加权声压级是根据人的听觉设计的，并且强调以1000 Hz为中心的高频声的贡献，因此可以给人一种控制方法对a加权声压级影响很小的印象。调制深度列在表3中，可以看到一个小的减小。值得注意的是，本研究中考虑的偏航和剪切相对较小，而在大剪切和偏航情况下，这些影响可能会大得多。此外，由于大气和尾迹变化所引起的噪声传播效应也不包括在内。未来，为了控制风力机远场噪声，将现有噪声源建模框架与传播模型[8]进一步耦合。

3 结论

  本文开发了一种先进的流-结构-声学框架，并对2.3MW NM80风电机在中等风切变、小偏航角和大偏航角下的负载场进行了测试，通过对结果的分析，总结出以下几点结论：

1. 基于Ellipsys3D/AL/Flex5耦合框架的仿真与2.3 MW NM80水轮机的现场负荷测量结果吻合较好。

2. 观察到风切变对流场有显著的影响，导致尾迹变弱。通过引入偏航降低了纵向风速，从而降低了声压级。

3. 在切变指数为0.3的中等风切变情况下，声压级的降低是通过调节来实现的，而功率系数和推力系数普遍变得更加波动。螺距调整技术仅对有风切变的情况有用。

4. 考虑到风力机噪声产生的原因繁多，声压级预测公式关系复杂，明显发现声压级与AoA之间并不是线性相关。通过比较AoA和SPL的变化也证实了这种非线性关系。

5. 通过对声压级和A计权声压级的比较可以看出，本文所实施的螺距控制主要影响低频的风力机噪声，而对高频噪声的影响不明显。

6. 平均声压级降低0.4 dB，调制深度略有降低。