文献解读：大气条件对风电机组次声测量的影响

题目：大气条件对风电机组次声测量的影响
关键词：风电机组次声；叶片通过频率等级；预测模型；大气湍流；室外次声测量；

1 中文摘要

  随着风电机组的规模和数量不断增加，过去十年中，人们对风电机组低频和次声的研究更加关注。但大气条件对风电机组噪声影响的研究较少，如大气边界层的湍流特征等。本文进行一项详细的长期测量活动，结合风电机组附近次声记录和三个高度的高分辨率气象参数。基于测量数据开发人工神经网络（ANN）模型，模型可预测叶片通过频率水平和宽带次声噪声，并能够在很大范围的大气条件下区分风电机组发出的宽带入流噪声和圆顶防风罩下剩余的麦克风引起的风噪声。同时，人工神经网络可以推导气象和湍流参数与风电机组发射的次声成分之间的物理关系。最后指出次声产生的主要预测因子是平均风速、湍流强度和湍流垂直热通量。

2 关键信息提取

2.1 引言

风电机组尺寸的不断增大，可能会导致噪声频谱向低频方向移动。

  在次声范围内由风电机组产生的压力波动会产生离散频率和宽带分量。
(1)对于现代大型水平轴风电机组，离散频率与叶片通过频率相关，通常低于1Hz。它的谐波通常在整个次声范围内占主导地位。叶片通过频率（BPF，blade passing frequency）水平决定了风电机组的声学特征。
(2)宽带分量，通常表示为流入噪声，也覆盖了整个次声频率范围，直到极低的频率，进入可听频率范围的较低部分。（注：本文中“次声”指频率低于20Hz。“可听频率”指超过20Hz。“低频”指的大约100Hz以下。

  公认BPF水平是由于旋转叶片和塔筒之间的空气动力学相互作用产生。对于下风向风电机组，由于塔身前部的入风速度降低，阻碍了进入的气流。这种局部速度扰动会导致经过叶片的迎角发生变化，气动载荷发生周期性变化，BPF处的压力水平离散。BPF噪声产生机制仍未完全证实。假设叶片-塔相互作用噪声可归因于叶片产生的气动扰动和对塔的影响。通过数值模拟，可以确定塔是BPF噪声的主要压力产生点。BPF水平的其他来源也可以在大气湍流、侧风和风切变中确定，这些都会导致旋转叶片的周期性气动变化。
【参考文献】
[1] Yendrew Yauwenas, Branko Zajamšek, John Reizes, Victoria Timchenko, Con J. Doolan; Numerical simulation of blade-passage noise. J. Acoust. Soc. Am. 1 September 2017; 142 (3): 1575–1586. https://doi.org/10.1121/1.5003651
[2] Branko Zajamsek, Yendrew Yauwenas, Con J. Doolan, Kristy L. Hansen, Victoria Timchenko, John Reizes, Colin H. Hansen,
Experimental and numerical investigation of blade–tower interaction noise,Journal of Sound and Vibration,Volume 443,2019,Pages 362-375,ISSN 0022-460X,https://doi.org/10.1016/j.jsv.2018.11.048.

  风电机组入流噪声是由旋转结构与大气边界层中存在的入流湍流相互作用产生的。特别是，较大的入流湍流是次声入流噪声的原因。当涡流比平均叶弦大得多时，旋转叶片的载荷会发生突然变化，产生宽带次声，其频率与湍流涡流和叶弦的尺寸有关。对于大型现代风力涡轮机，这种机制影响次声范围的最低部分。对于小于叶片弦的流入湍流涡流，压力波动是由叶片表面的涡流局部产生的，并且可以出现在次声频谱的剩余部分，直至可听频率范围的最低部分。风切变和侧风条件也会引起旋转叶片气动载荷的变化。在过去的几十年里，该部分研究主要集中在通过数值或半经验模型来研究入流噪声。

  风电机组次声排放测量不容忽视，它与室外高水平的风致麦克风噪声共存。虽然理论上BPF水平可以很容易地与宽带噪声区分开来，但风致麦克风噪声可以完全掩盖对风力涡轮机次声的两种贡献，即使在低平均风速下也是如此。在评估风电机组次声排放的测量中，常用圆顶风罩。
【参考文献】
[3] Sarah D'Amico, Timothy Van Renterghem, Dick Botteldooren,Measuring infrasound outdoors with a focus on wind turbines: the benefits of a wind-shielding dome,Applied Acoustics,Volume 178,2021,108015,ISSN 0003-682X,https://doi.org/10.1016/j.apacoust.2021.108015.

  Buck等（2016）将实测的风力机入流噪声与由转子叶片振动确定的局部湍流度相关联，发现在低频处存在正相关关系。然而，后一项研究仅限于可听频率范围。没有研究发现允许基于（流入）大气参数来预测次声的产生。
【参考文献】
[4]Steven Buck, Stefan Oerlemans, Scott Palo,Experimental characterization of turbulent inflow noise on a full-scale wind turbine,Journal of Sound and Vibration,Volume 385,2016,Pages 219-238,ISSN 0022-460X,https://doi.org/10.1016/j.jsv.2016.09.010.

2.2 测试

  2019年8月—2019年12月 和 2020年3月—2020年11月在根特大学地形上的Melle风电场进行。声压级排放与气象数据同时测量。测量位置的风电场由三个Enercon E82风电机组组成，每个机组容量为2.3MW，三叶片，可变桨距，轮毂高度为108m，风轮直径为82m，额定风速14m/s，切入风速2m/s。位于西北-东南方向，彼此相距约450米，如图1所示。周围环境为平坦的农业地形，一些稀疏的建筑位于距离麦克风200米的地方，大约250米的地方有一条主要的高速公路。

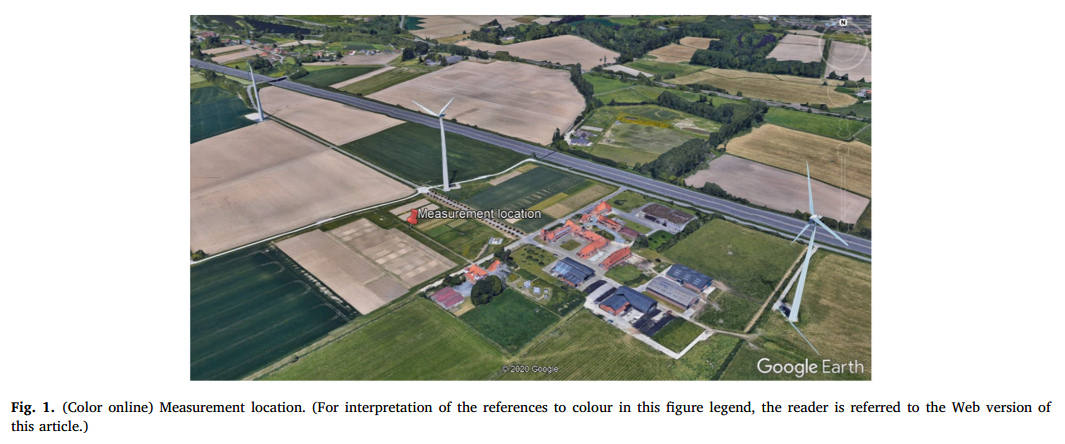
  采用GRAS 46az低频传声器和前置放大器进行测量。该设备可确保0.5Hz的线性响应，灵敏度为50mV/Pa。使用Alix System单板计算机，采样频率为48kHz，连续57s录音。每次记录后暂停3秒，以便有时间保存数据。GPS时钟每分钟同步一次录音。该设备采用直连电源供电。使用Svantek 30a级1级声学校准器对麦克风进行1kHz和94dB的校准；每周重复记录校准信号。

  麦克风配有防雨装置和直径10cm的标准泡沫防风罩。为了进一步降低风致麦克风噪声，提高次声信噪比，增加了一个2.2m高、3.2m基底直径的防风圆顶。如前所述，穹顶的设计和验证细节（D ' Amico等人，2021年）。麦克风放置在距离中间风力涡轮机120m，距离地面0.5m的位置。按照IEC61400-11，将麦克风平装在刚性板上是测量风电机组噪声（可听）的常用方法，但在这种长期无人看守的室外测量装置中，没有遵循这种方法来避免麦克风受到水的损坏。由于地面在次声频率范围内可以被认为是完全刚性的，因此仍然可以观察到地面反射的压力加倍。
【参考文献】
[5]Sarah D'Amico, Timothy Van Renterghem, Dick Botteldooren,
Measuring infrasound outdoors with a focus on wind turbines: the benefits of a wind-shielding dome,Applied Acoustics,Volume 178,2021,108015,ISSN 0003-682X,https://doi.org/10.1016/j.apacoust.2021.108015.

  气象资料分别在海拔2、10和108m处获取。Gill WindMaster 3D声速风速仪位于10米高度，以20Hz的频率获取风数据，测量精度为0.01 m/s，温度为0.01◦C。风速计提供风速模量(U)、风向、风速垂直分量(w)、声速和气温(T)的瞬时值（Burns et al, 2012）。
2m高度的气象数据由根特大学物理与天文学系（Caluwaerts et al ., 2020）提供，在距离麦克风40m的气象站获取。该数据以1分钟为基础。
108m高度（轮毂高度）的数据由风电场运营商每10分钟提供一次，既是气象数据，也是风机运行数据。2和108m高度的气象资料包括平均风速（MWS）、风速标准差（StdWS）、风向和气温。2 m高度的数据还包括空气湿度和降水，轮毂高度的风力机数据提供了三台风力机的功率、转速和机舱位置。

2.3 结果与讨论

名词定义：
功率谱密度：The power spectral densities (PSDs)
湍流强度：The turbulence intensity (TI)
平均风速：mean wind speed (MWS)

2.3.1 BPF水平受气象影响

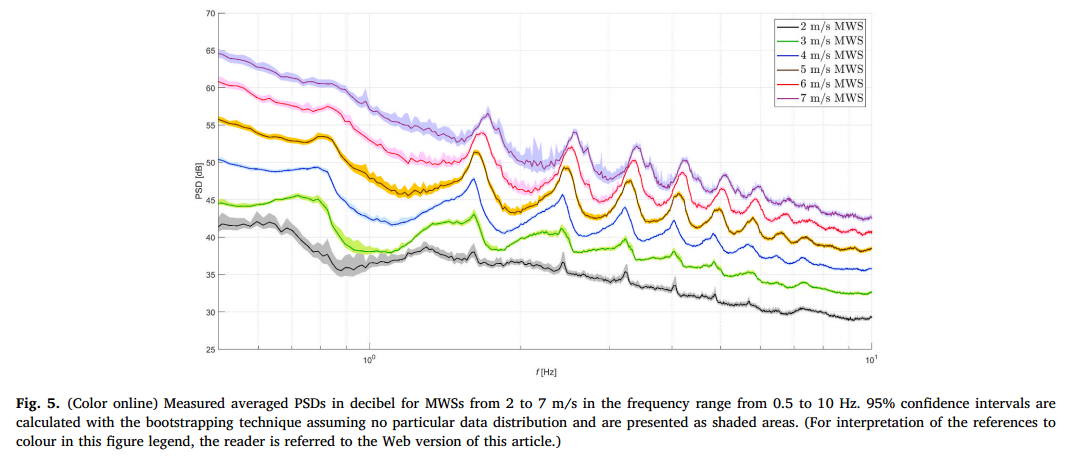
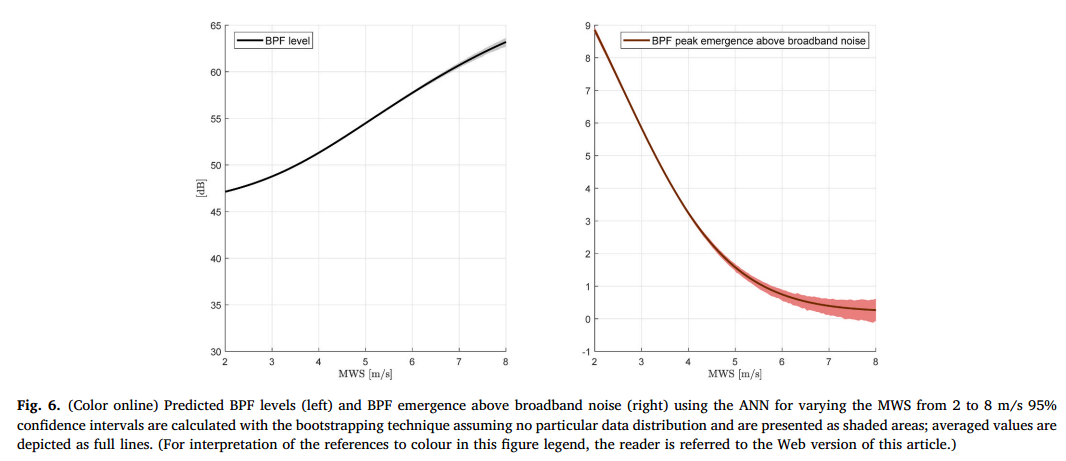
  不同MWSs的测量平均psd如图5所示，而图6显示了不同MWSs的预测BPF水平及其在宽带噪声之上的出现。测量结果允许跟踪BPF峰值及其与MWS的谐波的演变。离散分量电平和宽带噪声电平都随着MWS的增加而增加。在所有MWSs中，BPF峰值的一系列谐波都清晰可见。相反，基本的BPF峰值电平大多接近宽带噪声电平。对于低MWSs，可以检测到BPF峰值，而对于最高MWSs，这些峰值几乎完全淹没在捕获的宽带噪声中。
  从图6可以看出，随着MWS的增加，预测的BPF峰值增加，而在宽带噪声以上出现的BPF峰值随着MWS的增加而减少。这主要是因为BPF附近的宽带噪声（图10）随着MWS的增加而急剧增加。

  对于不同的MWSs和TI值，BPF电平和BPF出现在宽带噪声之上的预测值如图7所示。湍流能量的增加导致所有MWSs宽带以上BPF水平的增加和BPF出现的减少。事实上，宽带噪声也受到TI的积极影响。

2.3.2 MWS和TI对入流噪声的影响

  图10给出了四个不同频率范围（0.5-10Hz, 0.5-1Hz， 1-5Hz和5-10Hz）的宽带噪声和流入噪声预测与MWS的关系。与BPF峰值分析相比，宽带分量不仅来自风力机入流噪声，还来自风致麦克风噪声，这些噪声仍然存在于风屏蔽圆顶下方。考虑到它们相似的频谱，两者都不容易被挑出来。
  在图10的左侧可以观察到开、关两种情况下宽带噪声级的差异。它的范围从2m/s MWS时的约2dB到8m/s MWS时的约5db。按照式（10）对纯流入噪声进行分离，如图10的右侧所示。尽管信噪比通常很小，甚至为负值，但图10中所示的有限置信区间，对于打开和关闭条件，都允许有意义地扣除（纯）风力涡轮机流入噪声，这是这里主要关注的。在本文的其余部分中，将只表示纯流入图。

  对于图10所示的所有频率范围，流入噪声以及宽带噪声随着MWS的增加而增加。在0.5 ~ 1Hz的频率范围内，也存在BPF，流入噪声和宽带噪声都随着MWS的增加而急剧增加。可见，风力机在最低频率范围内产生的入流噪声会受到较大的大气湍流的强烈影响，而越大的MWSs越一致（见图11），导致较低频率范围内的入流噪声增加比其他范围更强。因此，随着MWS的增加，风电机组宽带噪声的增幅高于BPF峰值水平（图6），导致增加MWS时，BPF出现的预测值低于宽带噪声（图6）。

  图11给出了不同TI下风电机组进水噪声预测的变化趋势。对于几乎所有的MWSs，从0到55%TI，在0.5到1Hz的频率范围内，流入噪声的增加大约是预测BPF水平增加的两倍（图7）。在考虑的所有频率范围内，流入噪声对TI的依赖性是相似的，由于TI与湍流漩涡中所含的能量之间的直接关系，从0到55% TI的变化略小于10 dB。如图10所示，在最低频率范围内（0.5-1 Hz），电平比其他范围更依赖于MWS。

2.3.3 赫尔曼指数对入流噪声的影响

  图12显示了四个不同频率范围和不同MWSs下Hellmann指数对入流噪声的影响。赫尔曼指数越高，两个最高频率范围（1-5Hz和5-10Hz）的入流噪声越高。至于BPF水平（图8），这些频率范围内的流入噪声受到转子平面上MWSs差异的影响。在最低频率范围内（0.5-1Hz），入流噪声对Hellmann指数的依赖性不显著。虽然赫尔曼指数与MWS的垂直变化密切相关，但这与导致频率高达1hz的次声产生的非常大的湍流漩涡的形成没有直接联系。

2.3.4 垂直热流密度和垂直温度梯度的影响

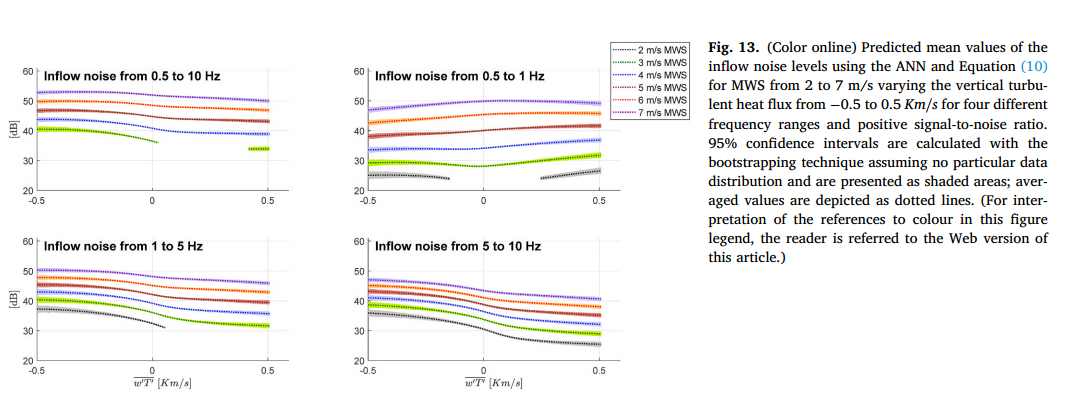
  紊流垂直热通量和温度梯度对预测入流噪声的影响分别如图13和图14所示。观察垂直湍流热通量下入流噪声的行为（图13），可以注意到，在垂直湍流热通量为正值的不稳定大气条件下，所有MWSs在0.5 ~ 1Hz频率范围内的入流噪声水平都有所增加。在其他频率范围内，垂直湍流热通量为正值时，水平降低。入流噪声在不同频率范围内的不同表现表明在不同频率范围内起作用的噪声产生机制不同，但要明确解决这些问题仍然是一项艰巨的任务。垂直热不稳定性可能与大湍流的形成有关。这些产生了风力涡轮机的大型旋转结构的载荷变化，导致声发射在次声频谱的最低部分。据推测，当大气变得更加稳定时，湍流漩涡的大小减小，在叶片表面产生局部压力变化，从而导致更高次声频率（1-5 Hz和5-10Hz）的更高发射。垂直温度梯度在不同频率范围内对入流噪声水平的影响并不大（图9），在三台风机运行时几乎保持不变。

3 结论

  在一些风电机组附近进行了长期的测量活动，获得了详细的声学和气象数据。推导了大范围大气条件下的平均PSD。大量的数据可以训练一个人工神经网络程序，然后用来预测BPF水平和风电机组在测量位置次声范围内的宽带噪声级（即入流噪声）。

（1）人工神经网络能够提供稳定的次声预测，并具有较高的确定系数。同时，人工神经网络允许区分流入噪声（由风电机组机产生）和屏蔽圆顶下剩余的风诱导麦克风噪声，依靠对涡轮机“开”和“关”周期的了解，即使在有限的时间内负信噪比。

（2）BPF水平和入流噪声都受到MWS和TI的强烈影响。高MWS和TI值会导致BPF和流入噪声水平增加。在考虑的最低频率范围内（0.5-1Hz），风电机组产生的宽带噪声在MWS和TI的作用下比在其他范围内增加得更大。最低频率范围内的流入噪声随着MWS和TI的增大而增大BPF峰值水平，减少它们在高MWSs和TI的入流噪声中出现。

（3）垂直湍流热通量对入流噪声的影响很大，特别是在考虑的最低频率范围内。正湍流热通量导致来自风力涡轮机的流入噪声量增加，表明在0.5至1Hz的频率范围内湍流产生的噪声占主导地位。

（4）从垂直风切变的影响分析中可以看出，Hellmann指数值越大，表明风速水平分量的垂直梯度越大，导致BPF水平增加，而四个不同频率范围内的入流噪声水平受Hellmann指数的影响较小。