主席树（填坑）

引入：

线段树：每个节点维护一段区间的信息，叶子节点代表第几个数

权值线段树：

　　维护数组元素出现的次数

　　用途：（1）每个节点维护一个区间 数 出现的次数，可被查询

　　（2）可以快速找到K-th

　　（3）查询某数出现的次数

主席树：

　　需求：离散化，二分，

　　用途：查询 K - th ，数 X 排第几 ， 查询若干数组的排序，数X相邻的数的值

　　思想：主席树是怎么维持可持久化的呢？如果直接建若干棵树，第i棵树表示第i次操作后的状态，也就是第i棵树维护的是区间【1，i】中每个数出现的次数，就会出现MLE。绘图会发现，在每次修改时，两个子节点中只有一个会被修改，也就是说一次修改只会有 logn 个节点被修改，那么显然所有节点都新建备份是多余的。那么可以让修改后的树跟修改前的树共享节点来降低空间以及时间的使用

时间复杂度：

　　离散化：nlogn，

　　建空树：nlogn

　　更新点：nlogn + nlogn = nlogn

　　查   询：mlogn

　　综   合：（m+n）logn

空间复杂度：

　　nlogn

 

P3919 【模板】可持久化线段树 1（可持久化数组）

 

 

 

 

 

 

 

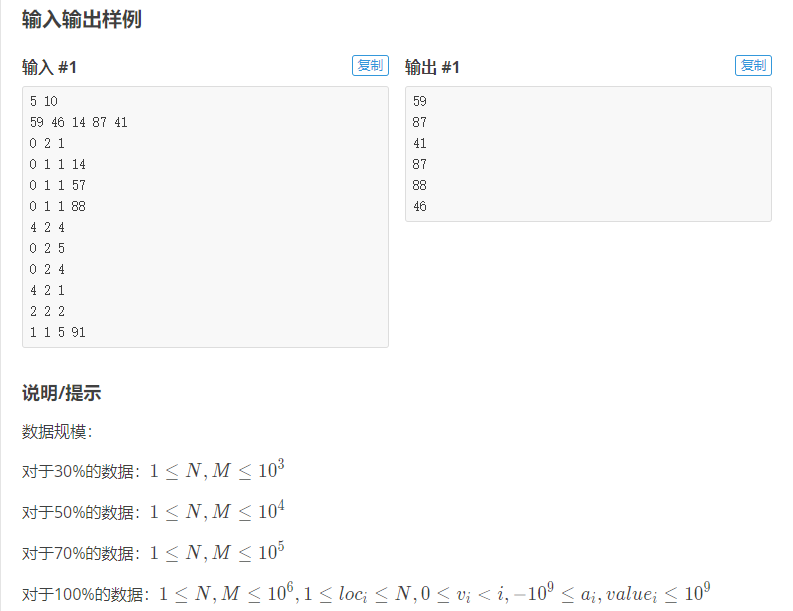
#include <bits/stdc++.h>
using namespace std;
const int mxn = 24e6+7 ;
#define ll long long
#define eps 1e-5 
#define open freopen("input.in","r",stdin);freopen("output.in","w",stdout);
int rd(){
    int x = 1, y = 0 ; char c = getchar();
    while(!isdigit(c)) {if(c=='-') x = -1 ; c = getchar();}
    while(isdigit(c)) {y = (y<<1) + (y<<3) + (c^48);c = getchar();}
    return x*y;
}
int n,m,t,k,ans,cnt,p;
int si;/// 节点个数 
int a[mxn] , b[mxn] ,id[mxn] , sum[mxn] , lc[mxn] , rc[mxn] , val[mxn];
////数据，离散数据，每颗线段树根节点编号 ，节点权值,记录左右子节点
void build(int &x,int l,int r)
{
    x = ++si ; ///增加节点
    if(l==r){ val[x] = a[l] ;  return ;}
    int mid = (l+r)>>1;
    build(lc[x],l,mid); build(rc[x],mid+1,r);
}
void update(int &x,int pre,int l,int r,int loc,int value)
{
    x = ++si;
    lc[x] = lc[pre] , rc[x] = rc[pre] , val[x] = val[pre] ;
    if(l==r) {val[x]=value;return;}
    int mid = (l+r)>>1;
    if(loc<=mid) update(lc[x],lc[pre],l,mid,loc,value);
    else update(rc[x],rc[pre],mid+1,r,loc,value);
}
int query(int &x,int l,int r,int loc)
{
    if(l==r) return val[x];
    int mid = (l+r)>>1;
    if(loc<=mid) return query(lc[x],l,mid,loc);
    else return query(rc[x],mid+1,r,loc);
}
void solve() 
{
    n = rd() , m = rd() ;
    for(int i=1;i<=n;i++) a[i] = rd();
    build(id[0],1,n);
    for(int i=1;i<=m;i++){
        int v = rd() , op = rd() , loc = rd() ;
        if(op==1){
            int value = rd();
            update(id[i],id[v],1,n,loc,value);
        } else {
            printf("%d\n",query(id[v],1,n,loc));
            id[i] = id[v] ;
        }
    }
}
int main()
{
    /// open
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    solve();
}

 

经典的主席树入门题——静态区间第 $k$ 小

 

 

 

代码：

#include <bits/stdc++.h>
using namespace std;
const int mxn = 5e6+7 ;
#define ll long long
#define eps 1e-5 
#define open freopen("input.in","r",stdin);freopen("output.in","w",stdout);
int rd(){
    int x = 1, y = 0 ; char c = getchar();
    while(!isdigit(c)) {if(c=='-') x = -1 ; c = getchar();}
    while(isdigit(c)) {y = (y<<1) + (y<<3) + (c^48);c = getchar();}
    return x*y;
}
int n,m,t,k,ans,cnt,p;
int si;/// 节点个数 
int a[mxn] , b[mxn] ,id[mxn] , sum[mxn] , lc[mxn] , rc[mxn];
////数据，离散数据，每颗线段树根节点编号 ，节点权值,记录左右子节点
void build(int &x,int l ,int r)
{
    x = ++si;  sum[ x ] = 0 ;
    if(l==r) return ;
    int mid = (l+r)>>1;
    build(lc[x],l,mid); build(rc[x],mid+1,r);
}
int update(int x,int l,int r)
{
    int nx = ++si;
    lc[nx] = lc[x] , rc[nx] = rc[x] , sum[nx] = sum[x] + 1 ;
    if(l==r) return nx;
    int mid = (l+r)>>1;
    if(mid>=p) lc[nx] = update(lc[nx],l,mid);
    else rc[nx] = update(rc[nx],mid+1,r);
    return nx;
}
int query(int li,int ri ,int l,int r, int k)
{
    int mid = (l+r)>>1 , x = sum[ lc[ri] ] - sum[ lc[li] ] ;
    if(l==r) return l;
    if(x>=k) return query(lc[li],lc[ri],l,mid,k);
    else return query(rc[li],rc[ri],mid+1,r,k-x);
}
void solve() 
{
    n = rd() , m = rd() ;
    for(int i=1;i<=n;i++)
        a[i] = rd() , b[i] = a[i] ;
    sort(b+1,b+1+n);
    int num = unique(b+1,b+1+n) - b - 1 ;
    build( id[0] , 1 , num );
    for(int i=1;i<=n;i++){
        p = lower_bound(b+1,b+1+num,a[i])-b;
        id[i] = update(id[i-1],1,num);
    }
    while(m--){
        int l = rd() , r = rd() , k = rd() ;
        cout<<b[ query(id[l-1],id[r],1,num,k) ]<<endl;
    }
}
int main()
{
    /// open
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    solve();
}

 

 

K-th NumberPOJ - 2104 

 题解：

#include <iostream>
#include <map>
#include <vector>
#include <queue>
#include <string>
#include <set>
#include <algorithm>
#include <cstring>
#include <string>
#include <vector>
#include <map>
#include <set>
#include <list>
#include <deque>
#include <queue>
#include <stack>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <iomanip>
#pragma GCC optimize(2)
using namespace std;
const int inf=0x3f3f3f3f;
#define ll long long
#define ull unsigned long long
const int mod = 1e9+7;/// 998244353;
const int mxn = 5e6 +7;
const int N = 8e4 + 7 ;
int _ , n , m , t , k , ans , cnt , si ;
template <class T>
void rd(T &x){
    T flag = 1 ; x = 0 ; char ch = getchar() ;
    while(!isdigit(ch)) { if(ch=='-') flag = -1; ch = getchar(); }
    while(isdigit(ch)) { x = (x<<1) + (x<<3) + (ch^48); ch = getchar(); }
    x*=flag;
}
int lc[mxn] , rc[mxn] , a[mxn] , b[mxn] , T[mxn] , sum[mxn] ;
void build(int &id,int l,int r)
{
    id = ++si , sum[id] = 0 ;
    if(l==r) return ;
    int mid = (l+r)>>1;
    build(lc[id],l,mid) , build(rc[id],mid+1,r);
}
int update(int pre,int l,int r,int p)
{
    int nx = ++si ;
    lc[nx] = lc[pre] , rc[nx] = rc[pre] , sum[nx] = sum[pre] + 1 ;
    if(l==r) return nx;
    int mid = (l+r)>>1 ;
    if(mid<p) rc[nx] = update(rc[nx],mid+1,r,p);
    else lc[nx] = update(lc[nx],l,mid,p);
    return nx ;
}
int query(int li,int ri , int l,int r,int k)
{
    int x = sum[ lc[ri] ] - sum[ lc[li] ] ;
    int mid = (l+r)>>1;
    if(l==r) return l;
    if(x>=k) return query(lc[li],lc[ri],l,mid,k);
    else return query(rc[li],rc[ri],mid+1,r,k-x);
}
void solve()
{
    rd(n) , rd(m) ;
    for(int i=1;i<=n;i++) rd(a[i]) , b[i] = a[i];
    sort(b+1,b+1+n);
    int lim = unique(b+1,b+1+n) - b - 1;
    build(T[0],1,lim);
    for(int i=1;i<=n;i++){
        int p = lower_bound(b+1,b+1+lim,a[i]) - b ;
        T[i] = update(T[i-1],1,lim,p);
    }
    int u , v , k;
    while(m--){
        rd(u) , rd(v) , rd(k) ;
        printf("%d\n",b[query(T[u-1],T[v],1,lim,k)]);
    }
}
int main()
{
    ios::sync_with_stdio(false); cin.tie(0) ; cout.tie(0);
    solve();
}