Educational Codeforces Round 86 (Rated for Div. 2) C. Yet Another Counting Problem

https://codeforces.com/contest/1342/problem/C

 

 

 

 

 

 

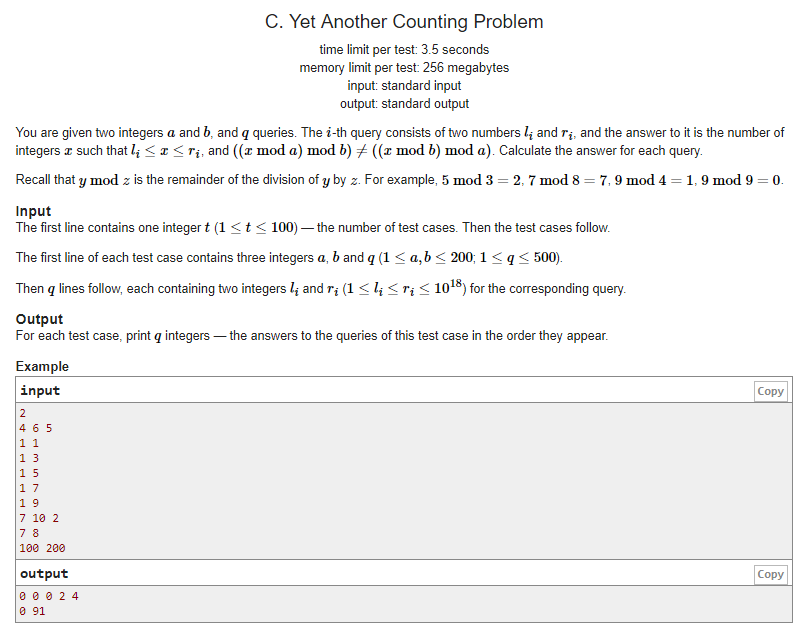
题意：给定的区间【L,R】中有多少个数可以满足( ( x mod a) mod b ) ≠ ( ( x mod b ) mod a )。

题解：暴力打表，n = a * b ，扫描1-n之间有多少数满足( ( x mod a) mod b ) ≠ ( ( x mod b ) mod a ) ，并记录下来。然后计算( R/n - (L-1)/n )*num[n] + num[R%n] - num[(L-1)%n] , 为什么是 L -1 呢， 是因为，x / n + num[ x % n] 计算的是x为终点的符合题意的数，而 L是包含在计算的区间内的，所以就要就算L-1区间

 

#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <vector>
#include <map>
#include <set>
#include <list>
#include <deque>
#include <queue>
#include <stack>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <iomanip>
#define ull unsigned long long
#define ll long long
#define pb push_back
#define mem(sum,x) memset(sum,x,sizeof(sum))
#define rep(i,start,end) for(int i=start;i<=end;i++)
#define per(i,end,start) for(int i=end;i>=start;i--)
#define tle ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
using namespace std;
const int mod = 1e9+7 ;
const int mxn = 1e6+7 ;
ull _,n,m,k,t,u,v,w,ans,cnt,ok;
int a[mxn] , num[mxn] , pre[mxn] , last[mxn] ;
int main()
{
    ull l , r , x ;
    int a, b ,q ;
    for(cin>>t;t;t--)
    {
        cin>>a>>b>>q;
        n = a*b;
        for(int i=1;i<=n;i++)
        {
            num[i]=num[i-1];
            if(i%a%b!=i%b%a) num[i]++;
        }
        while(q--)
        {
            cin>>l>>r;
            cout<<( r/n - (l-1)/n )*num[n] + num[r%n] - num[(l-1)%n]<<endl;
        }
    }
}