Codeforces Round #601 (Div. 2)

A. Changing Volume

 

Bob watches TV every day. He always sets the volume of his TV to bb. However, today he is angry to find out someone has changed the volume to aa. Of course, Bob has a remote control that can change the volume.

There are six buttons (−5,−2,−1,+1,+2,+5−5,−2,−1,+1,+2,+5) on the control, which in one press can either increase or decrease the current volume by 11, 22, or 55. The volume can be arbitrarily large, but can never be negative. In other words, Bob cannot press the button if it causes the volume to be lower than 00.

As Bob is so angry, he wants to change the volume to bb using as few button presses as possible. However, he forgets how to do such simple calculations, so he asks you for help. Write a program that given aa and bb, finds the minimum number of presses to change the TV volume from aa to bb.

Input

Each test contains multiple test cases. The first line contains the number of test cases TT (1≤T≤10001≤T≤1000). Then the descriptions of the test cases follow.

Each test case consists of one line containing two integers aa and bb (0≤a,b≤1090≤a,b≤109) — the current volume and Bob's desired volume, respectively.

Output

For each test case, output a single integer — the minimum number of presses to change the TV volume from aa to bb. If Bob does not need to change the volume (i.e. a=ba=b), then print 00.

Example

input

Copy

3
4 0
5 14
3 9

output

Copy

2
3
2

Note

In the first example, Bob can press the −2−2 button twice to reach 00. Note that Bob can not press −5−5 when the volume is 44 since it will make the volume negative.

In the second example, one of the optimal ways for Bob is to press the +5+5 twice, then press −1−1 once.

In the last example, Bob can press the +5+5 once, then press +1+1.

 

 

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int mxn = 1e6 + 5;
int n,m,k,t,vis[mxn];
int main()
{
    cin>>t;
    while(t--)
    {
        cin>>n>>m;
        if(n==m)
            cout<<0<<endl;
        else 
        {
            if( abs(n-m)%5==1 || abs(n-m)%5==2 )
                cout<<abs(n-m)/5+1<<endl;
            else if( abs(n-m)%5==3 || abs(n-m)%5==4 )
                cout<<abs(n-m)/5+2<<endl;
            else 
                cout<<abs(n-m)/5<<endl;
        }
    }
    return 0;
}

 

 

 

B. Fridge Lockers

 

Hanh lives in a shared apartment. There are nn people (including Hanh) living there, each has a private fridge.

nn fridges are secured by several steel chains. Each steel chain connects two different fridges and is protected by a digital lock. The owner of a fridge knows passcodes of all chains connected to it. A fridge can be open only if all chains connected to it are unlocked. For example, if a fridge has no chains connected to it at all, then any of nn people can open it.

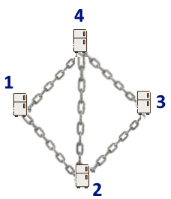For exampe, in the picture there are n=4n=4 people and 55 chains. The first person knows passcodes of two chains: 1−41−4 and 1−21−2. The fridge 11 can be open by its owner (the person 11), also two people 22 and 44 (acting together) can open it.

The weights of these fridges are a1,a2,…,ana1,a2,…,an. To make a steel chain connecting fridges uu and vv, you have to pay au+avau+av dollars. Note that the landlord allows you to create multiple chains connecting the same pair of fridges.

Hanh's apartment landlord asks you to create exactly mm steel chains so that all fridges are private. A fridge is private if and only if, among nn people living in the apartment, only the owner can open it (i.e. no other person acting alone can do it). In other words, the fridge ii is not private if there exists the person jj (i≠ji≠j) that the person jj can open the fridge ii.

For example, in the picture all the fridges are private. On the other hand, if there are n=2n=2 fridges and only one chain (which connects them) then both fridges are not private (both fridges can be open not only by its owner but also by another person).

Of course, the landlord wants to minimize the total cost of all steel chains to fulfill his request. Determine whether there exists any way to make exactly mm chains, and if yes, output any solution that minimizes the total cost.

Input

Each test contains multiple test cases. The first line contains the number of test cases TT (1≤T≤101≤T≤10). Then the descriptions of the test cases follow.

The first line of each test case contains two integers nn, mm (2≤n≤10002≤n≤1000, 1≤m≤n1≤m≤n) — the number of people living in Hanh's apartment and the number of steel chains that the landlord requires, respectively.

The second line of each test case contains nn integers a1,a2,…,ana1,a2,…,an (0≤ai≤1040≤ai≤104) — weights of all fridges.

Output

For each test case:

• If there is no solution, print a single integer −1−1.
• Otherwise, print a single integer cc — the minimum total cost. The ii-th of the next mm lines contains two integers uiui and vivi (1≤ui,vi≤n1≤ui,vi≤n, ui≠viui≠vi), meaning that the ii-th steel chain connects fridges uiui and vivi. An arbitrary number of chains can be between a pair of fridges.

If there are multiple answers, print any.

Example

input

Copy

3
4 4
1 1 1 1
3 1
1 2 3
3 3
1 2 3

output

Copy

8
1 2
4 3
3 2
4 1
-1
12
3 2
1 2
3 1

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int mxn = 1e6 + 5;
int n,m,k,t,vis[mxn];
int main()
{
    cin>>t;
    while(t--)
    {
        cin>>n>>m;
        vector<int>vc;
        ll ans= 0;
        for(int i=1;i<=n;i++)
        {
            cin>>k;
            //vc.insert(k);
            ans += k*2;
        }
        if(m<n || n==2)
            cout<<-1<<endl;
        else
        {
            cout<<ans<<endl;
            for(int i=1;i<=n;i++)
                cout<<i<<" "<<i%n+1<<endl;
        }
    }
    return 0;
}