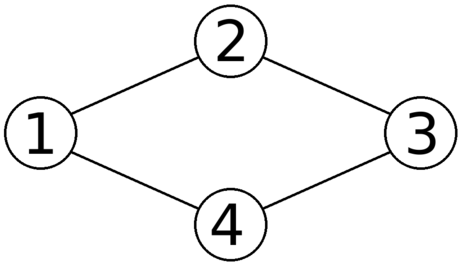
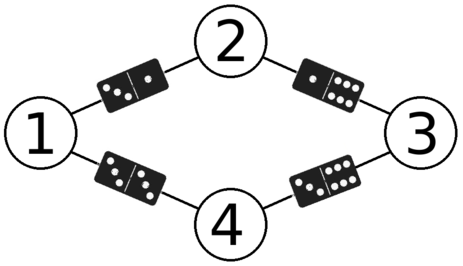
C. Anadi and Domino 《 Codeforces Round #588 (Div. 2) 》

Anadi has a set of dominoes. Every domino has two parts, and each part contains some dots. For every aa and bb such that 1≤a≤b≤61≤a≤b≤6, there is exactly one domino with aa dots on one half and bb dots on the other half. The set contains exactly 2121 dominoes. Here is an exact illustration of his set:

Also, Anadi has an undirected graph without self-loops and multiple edges. He wants to choose some dominoes and place them on the edges of this graph. He can use at most one domino of each type. Each edge can fit at most one domino. It's not necessary to place a domino on each edge of the graph.

When placing a domino on an edge, he also chooses its direction. In other words, one half of any placed domino must be directed toward one of the endpoints of the edge and the other half must be directed toward the other endpoint. There's a catch: if there are multiple halves of dominoes directed toward the same vertex, each of these halves must contain the same number of dots.

How many dominoes at most can Anadi place on the edges of his graph?

Input

The first line contains two integers nn and mm (1≤n≤71≤n≤7, 0≤m≤n⋅(n−1)20≤m≤n⋅(n−1)2) — the number of vertices and the number of edges in the graph.

The next mm lines contain two integers each. Integers in the ii-th line are aiai and bibi (1≤a,b≤n1≤a,b≤n, a≠ba≠b) and denote that there is an edge which connects vertices aiai and bibi.

The graph might be disconnected. It's however guaranteed that the graph doesn't contain any self-loops, and that there is at most one edge between any pair of vertices.

Output

Output one integer which denotes the maximum number of dominoes which Anadi can place on the edges of the graph.

Examples

input

Copy

4 4
1 2
2 3
3 4
4 1

output

Copy

4

input

Copy

7 0

output

Copy

0

input

Copy

3 1
1 3

output

Copy

1

input

Copy

7 21
1 2
1 3
1 4
1 5
1 6
1 7
2 3
2 4
2 5
2 6
2 7
3 4
3 5
3 6
3 7
4 5
4 6
4 7
5 6
5 7
6 7

output

Copy

16

Note

Here is an illustration of Anadi's graph from the first sample test:

And here is one of the ways to place a domino on each of its edges:

Note that each vertex is faced by the halves of dominoes with the same number of dots. For instance, all halves directed toward vertex 11have three dots.

 

 

#include <bits/stdc++.h>
using namespace std;
#define pb push_back
#define ppb pop_back
#define mp make_pair
#define masout for(int i = 0; i < n; i++ ) cout << a[i];return 0;
bool c[10][10];
int main () {
    int n, m;
    cin >> n >> m;
    for(int i = 0; i < m; i++ ) {int u,v;cin>>u>>v;c[u][v]=[v][u]=1;}
    if(n <= 6) cout << m, exit(0);
    int mn = 1e9;
    for(int i = 1; i <= 7; i++ ) 
　　 　　for(int j = 1; j <= 7; j++) 
　　　　 {
　　　　　　　　int x = 0; 
　　　　　　　　for(int k = 1; k <= 7; k++ ) 
　　　　　　　　　　if(c[i][k] && c[k][j]) x++; 
　　　　　　　　mn = min(mn , x);
　　　　 }
    cout << m - mn;
}

 

 

 

 

#include<bits/stdc++.h>
using namespace std;
typedef long long int LL;
#define sc(x) scanf("%d",&x)
#define scc(x,y) scanf("%d%d",&x,&y)
#define sccc(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define mkp(a,b) make_pair(a,b)
#define F first
#define pb(a) push_back(a)
#define S second
#define pii pair<int,int>
#define mem0(a) memset(a,0,sizeof(a))
#define mem(a,b) memset(a,b,sizeof(a))
#define MID(l,r) (l+((r-l)>>1))
#define ll(o) (o<<1)
#define rr(o) (o<<1|1)
const LL INF = 0x3f3f3f3f ;
const int maxn = 10000;
const double pi = acos(-1.0);
int T,n,m;
bool vis[10][10];
bool used[10][10];
int num[10];
int ans=0;
void dfs(int dep)
{
    if(dep==0)
    {
        mem0(used);
        int tmp=0;
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=n;j++)
            {
                if(i==j)continue;
                if(vis[i][j]==0)continue;
                if(used[num[i]][num[j]]==0)
                {
                    tmp++;
                    used[num[i]][num[j]]=1;
                    used[num[j]][num[i]]=1;
                }
            }
        }
        ans=max(ans,tmp);
        return ;
    }
    for(int i=1;i<=6;i++)
    {
        num[dep]=i;
        dfs(dep-1);
    }
}
int main()
{
    while(cin>>n>>m)
    {
        mem0(vis);
        int l,r;
        while(m--)
        {
            cin>>l>>r;
            vis[l][r]=vis[r][l]=1;
        }
        ans=0;
        dfs(n);
        cout<<ans<<endl;
    }
    return 0;
}