Convex Hull Trick
Problem:
Suppose that a large set of linear functions y = mix + bi is given along with a large number of queries. Each query consists of a value x and asks for the minimum of y(x) among all linear functions in the set.
Naïve algorithm:
If we evaluate y(x) for every function in each query and there are M lines in total, each query takes O(M) time. Thus, it takes O(MQ) time for Q queries.
Better algorithm:
However, we should see that sometimes that there are lines we don’t need. For example, a line that can’t produce the minimum value among all the lines in the set for all x value.
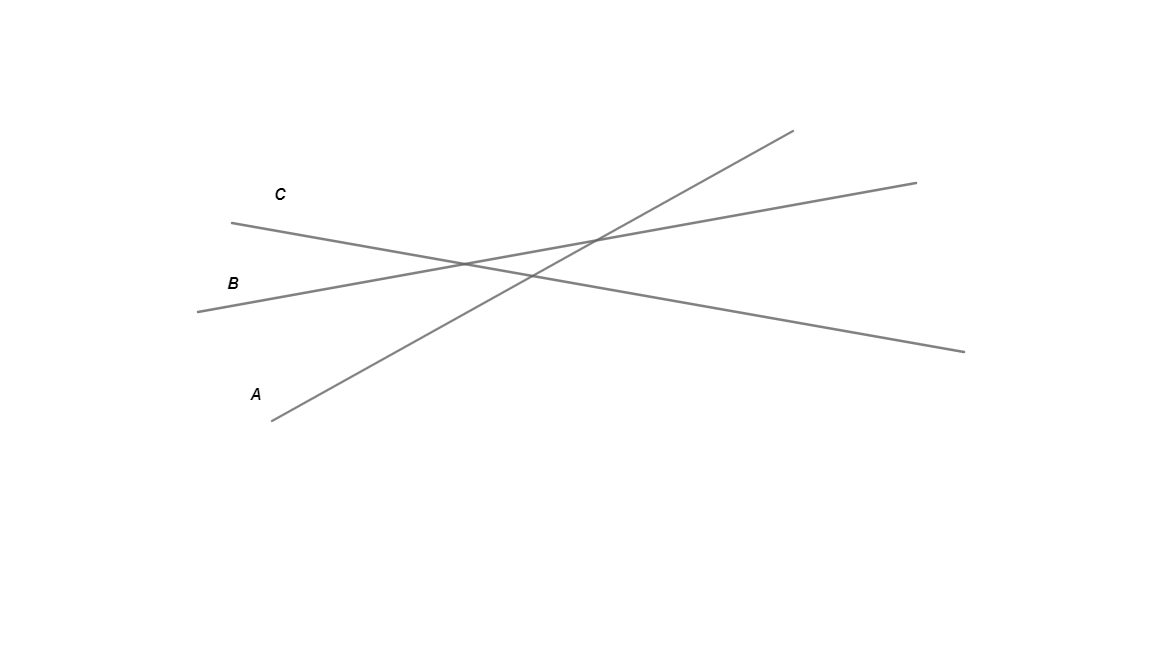
“B should be ignored since either A or C has a lower y value than B for all x.”
How can we find those lines to be deleted?
Let us first assume that all lines have different slopes. (Actually you can also handle the cases where there are lines with the same slope pretty easily.)
Then following is the claim:
l2 should be deleted if there exist l1 and l3 such that among the three lines l1 has the minimum slope, l3 has the maximum slope, and the intersection of l1 and l3 lies left to the intersection of l1 and l2.
This is an important observation, which allows us to develop some algorithm for deleting extra lines that we don’t need.
Then we should see another fact: when all the extra lines are deleted, the remaining lines will each obtain the minimum value in some interval among all lines, and the picture looks like the following:
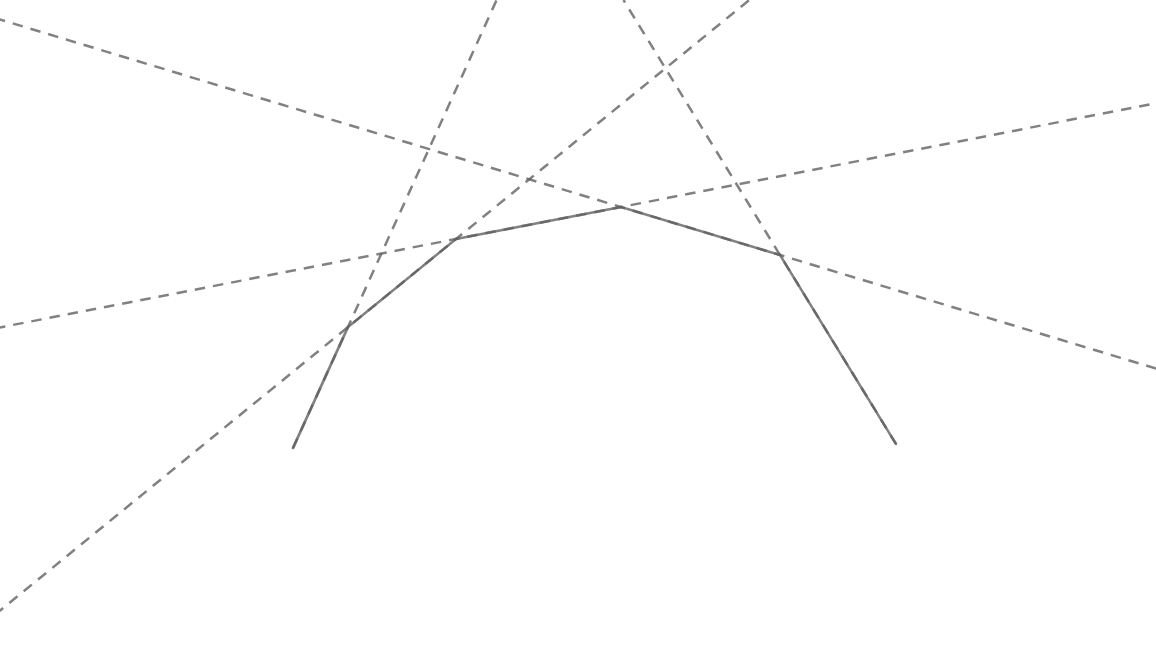
We can see that from left to right, the slope of the lines are monotonically decreasing, which reminds us of binary search (which we will discuss later).
What about sorting all the lines according to their slopes at the beginning? Then we can build the set of lines, the “convex hull”, by adding one line at a time and deleting the unneeded lines.
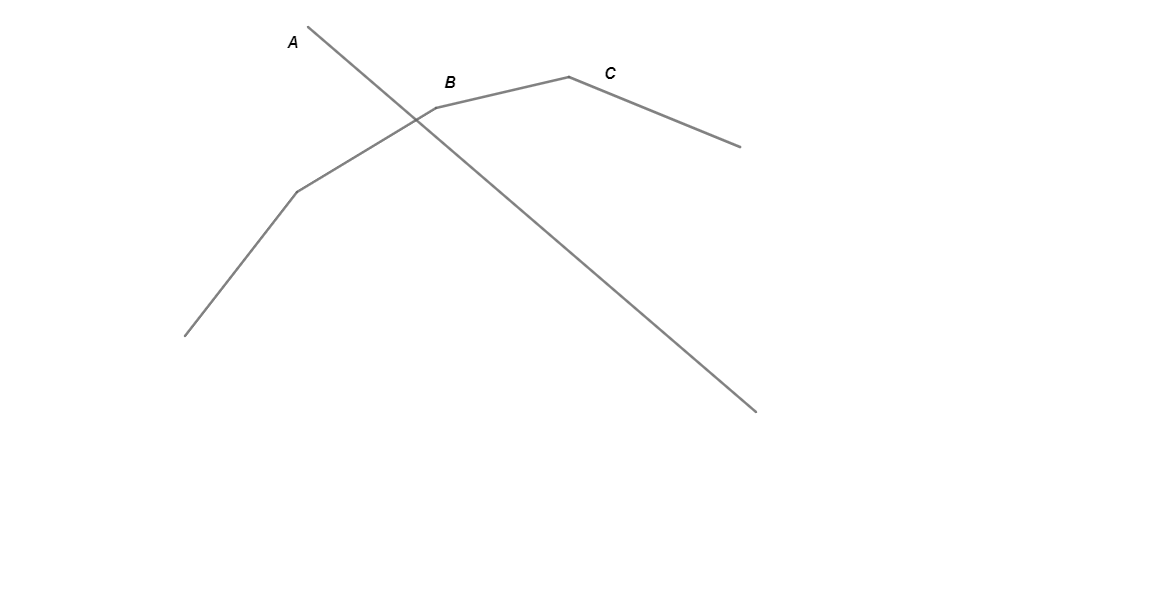
“When adding A, we need to delete B and C.”
This looks pretty nice, doesn’t it?
However, that’s not the whole story. In the method we come up with, we sorted all the lines beforehand, which we call an offline version, but sometimes we cannot sort all the lines beforehand, and we need to insert lines between the queries, and in that case, we need an online version of the algorithm.
Don’t worry! That’s still within our ability!
We can use binary search to split the original set of lines into two parts, the left with all the lines that has greater slopes, and the right with all the lines with less slopes.
First, we should check if l should be inserted or ignored.
If it needs to be inserted, we first insert it into left part (or right part), and delete the extra lines. Then we go to the right part to see which lines should be deleted. Notice that the lines to be deleted are always on a contiguous interval.
That’s all about constructing the “convex hull”. Then how can we calculate min(y(x)) for a particular x?
Actually, there are several approaches, but all of them get help from binary search.
- Store the starting position from which the line starts to obtain the minimum value, and find the right line.
- Perform binary search according to slopes, and find the right line.
The first approach is easy to understand, but a little bit hard to implement.
The second approach may sound a little bit confusing though, but actually is easier to implement. Here I will talk a little more on the second approach.
Since we store the lines in a set according to their slopes, it’s easy for us to get a line with some particular slope.
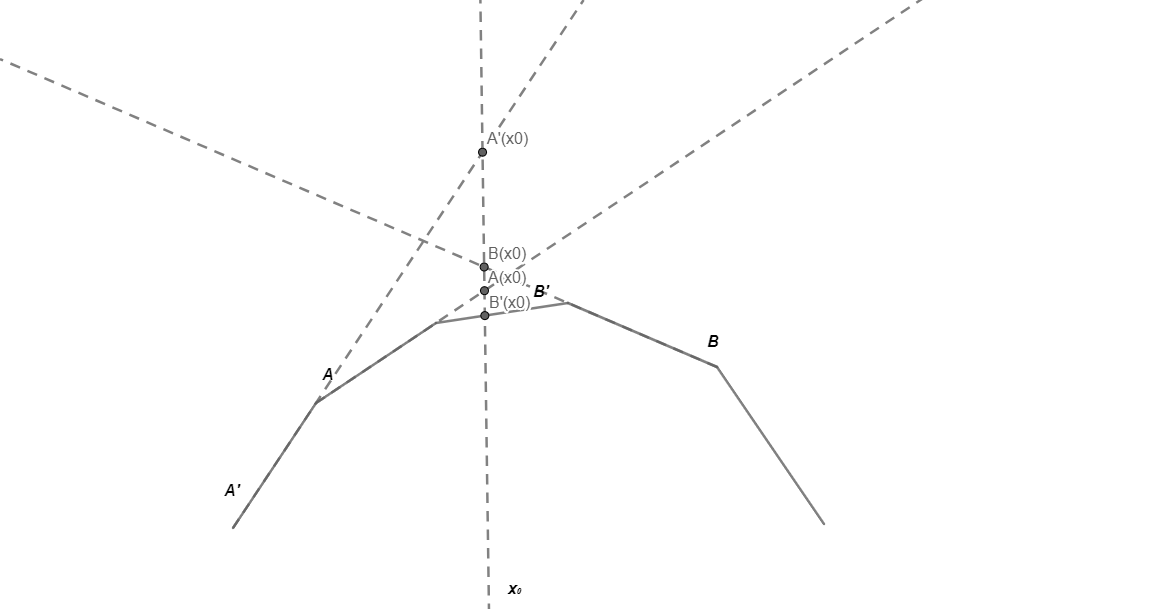
If we want to get min(y(x0)), we perform a binary search on the slopes, setting the upper bound to be INF and the lower bound to be -INF at the beginning.
If during the search we want to check if the line is the right line we are searching for, we can use the following method:
To check line A, we consider both A and A’.
At x0, we see that A(x0) is less than A’(x0), which tells us we should set the current slope to be the upper bound and search the right side (inclusive) to it.
To check line B, we consider both B and B’.
At x0, we see that B’(x0) is less than B(x0), which tells us we should set the current slope to be the lower bound and search the left side to it.
With this method, we can search for an answer relatively fast, with time complexity O(logM logK), where M is the number of lines and K is the maximum of slopes. Is this the best way to find the answer? We definitely can improve its performance.
As some of you may notice, there is one line in the convex hull on which we can obtain the minimum y value, and for all the line in the convex hull with a greater slope or less slope, we will obtain a greater y value. Not surprisingly, these values we obtain from different lines in the convex hull is also convex in some way, and we can use ternary search to find the line with the minimum y value. With this being said, this query can be sped up to O(logM), where M is the number of lines in the hull.
Above is a better solution to the problem presented at the beginning.
