6 矩阵的广义逆
关联：0 复习与引申、1 线性空间与线性变换、2 内积空间与等距变换、3 矩阵的相似标准形、4 Hermite二次型、5 范数及矩阵函数
本章目的
若已知\(AX=b\)，当\(A\)可逆时，方程组的解可表示为\(X=A^{-1}b\)。当\(A\)不可逆甚至不是方阵时，则需要利用广义逆来表示线性方程组的通解。
- 广义逆矩阵的概念
- 广义逆矩阵的计算
- 广义逆矩阵的性质
- 应用：不相容线性方程组的求解
广义逆矩阵的定义
※ 备注：这里的第三个、第四个方程分别代表\(AG\)和\(GA\)为\(Hermite\)阵。
即\(A\)和\(G\)地位平等，互为对方的广义逆矩阵。
- 设\(A \in C^{s \times n}\)，则\(A\)的广义逆矩阵是存在的，且是唯一的。\(A\)的广义逆记为\(A^+\)
广义逆矩阵A+的求法
- \(A^+=C^H(CC^H)^{-1}(B^HB)^{-1}B^H\)，其中\(A=BC\)为满秩分解。
- 特别地，若\(A\)行满秩，\(A^+=A^H(AA^H)^{-1}\)；若\(A\)列满秩，\(A^+=(A^HA)^{-1}A^H\)。
- 一些例子：
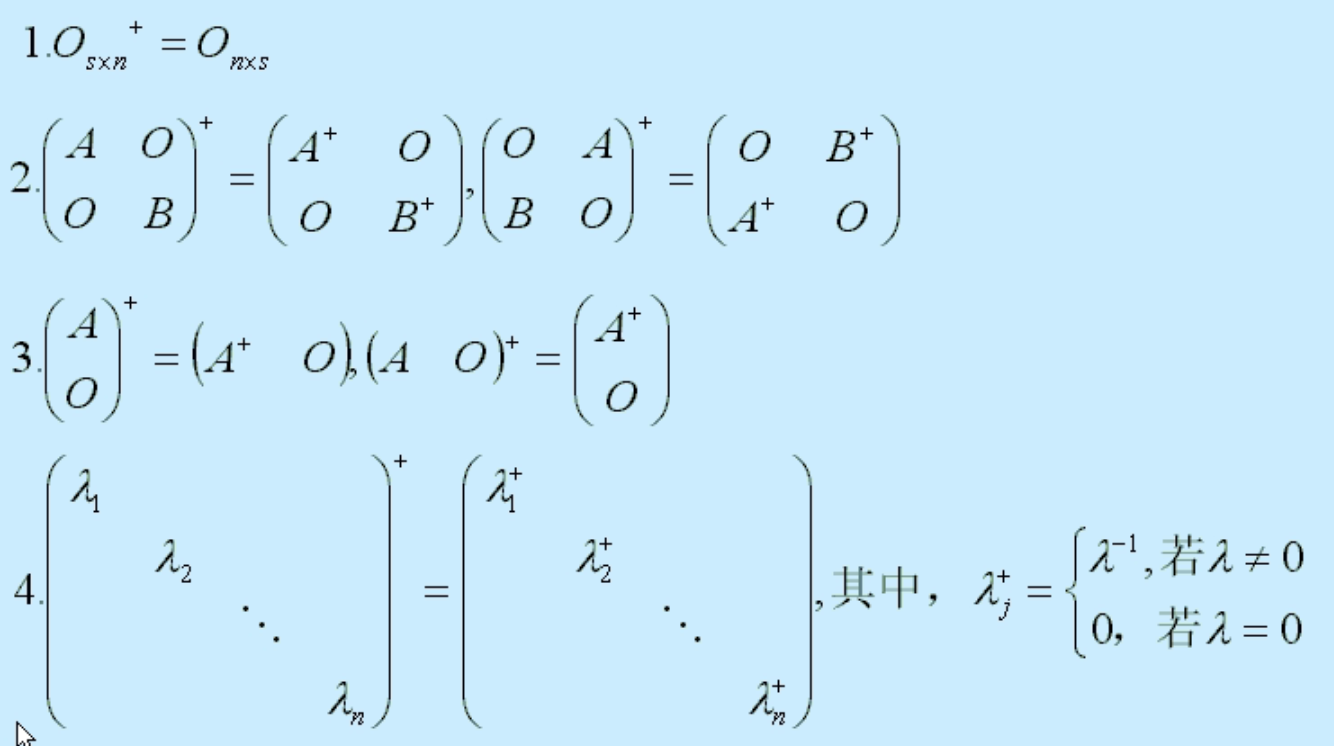
广义逆矩阵的性质
- 注：\((AB)^+ \neq B^+A^+\)
- 定理1：
- 定理2：
- 若\(A\)是正规阵，则\((A^2)^+=(A^+)^2\).
广义逆矩阵的应用
当线性方程组\(Ax=b\)无解时，如何求最好的近似解，即求\(x\)使得\(||Ax-b||_2\)最小。（即要找使\(Ax\)与\(b\)最“接近”之\(X\)）
最小二乘解
- 定理1：
- 定理2：
