4 Hermite二次型
关联:0 复习与引申、1 线性空间与线性变换、2 内积空间与等距变换、3 矩阵的相似标准形
本质上Hermite阵其实就是复数域下的对称阵,而酉矩阵对应复数域下的正交矩阵。
进而由对称阵又可以引出二次型以及与对角阵的合同。
Hermite阵、正规阵
Hermite二次型与Hermite矩阵
- 定义:

- 性质:

若 \(U\) 为酉矩阵,则 \(U^H=U^{-1}\)。
正规阵
- 定义:

- 定理:
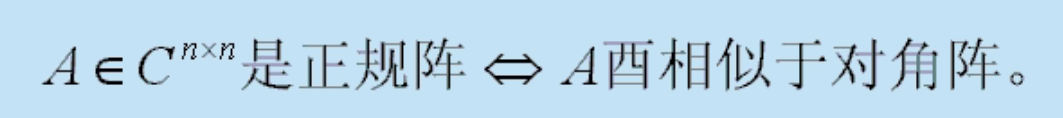
提到正规阵就要想到用酉矩阵把它变成对角阵。
- 推论:


幂零阵的特征值全部为0。若幂零阵同时还是正规阵的话,则该矩阵为 \(O\)。
Hermite二次型
共轭合同
-
可以证明:
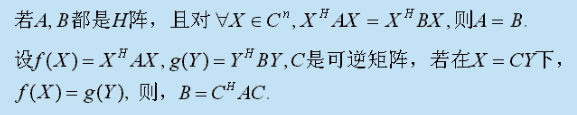
-
定义:

-
共轭合同满足:反身性、对称性、传递性。
标准形

- 在共轭合同意义下的标准形不唯一。
- 系数仅为1、-1和0的标准形称之为规范形。
惯性定理
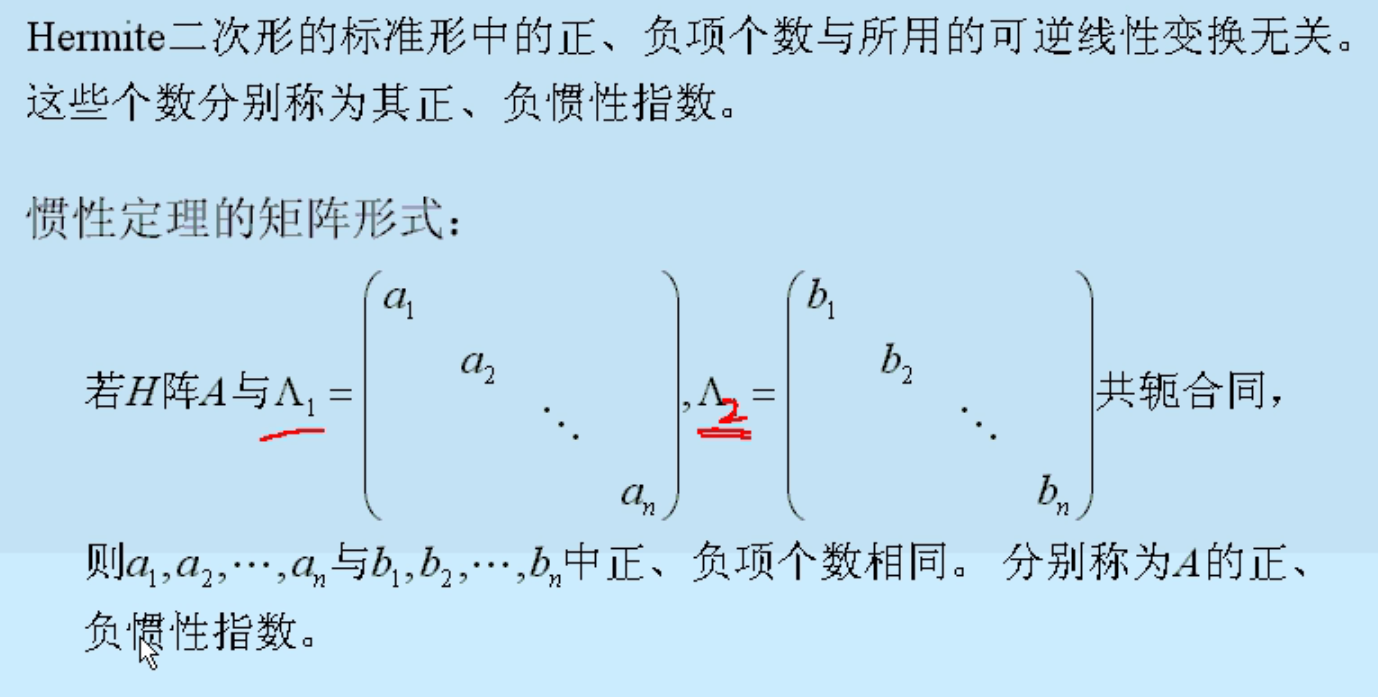
- 正惯性指数+负惯性指数=秩
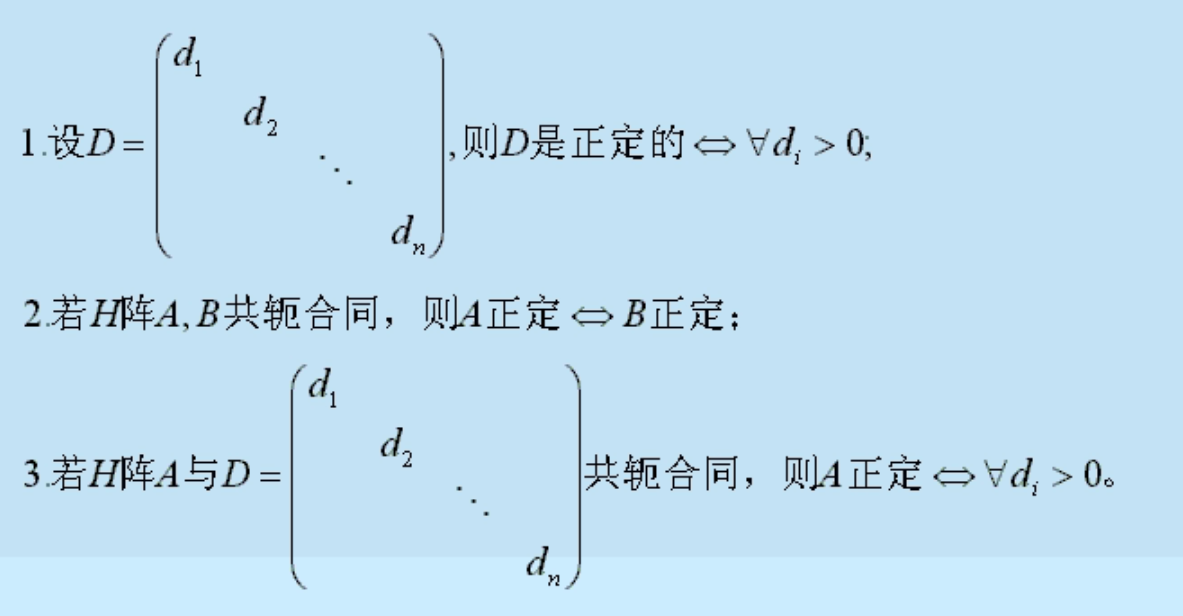
正定性
只有Hermite矩阵才会考虑正定性,所以在证明正定之前要先证明是Hermite阵。
- 如何建立判别方法:
- 一些等价命题(常用于判别正定):
- \(A\)是正定阵;
- 与\(A\)共轭合同的是正定阵;
- \(A\)的正惯性指数为n;
- \(A\)的特征值全大于零;
- \(A=S^2\),其中\(S\)为正定阵;
- \(A=P^HP\),其中\(P\)为可逆阵,即\(A\)共轭合同与单位阵\(I\);
- \(A\)的各顺序主子式均大于零;
- 若酉矩阵\(A\)是正定的,则\(A=I\)。
- 其他正定性:

正定矩阵与半正定矩阵的和一定是正定矩阵。
- 关于半正定阵的等价条件:

注意这里第四条并未限制矩阵\(P\)是否为可逆方阵,第五条是“各主子式”而非“各顺序主子式”。
奇值分解
它在矩阵的广义逆中有用。
- 推论(方阵的极分解)
Rayleigh商
可以利用\(X^HAX\)的值来研究\(A\)的特征值。
- 定义:

不难看出,若\(X_0\)是\(A\)的特征值\(\lambda_0\)对应的特征向量,则\(R(X_0)\)的值为\(\lambda_0\)。另外\(Hermite\)阵的\(Rayleigh\)商之值是实数。
- 定理:
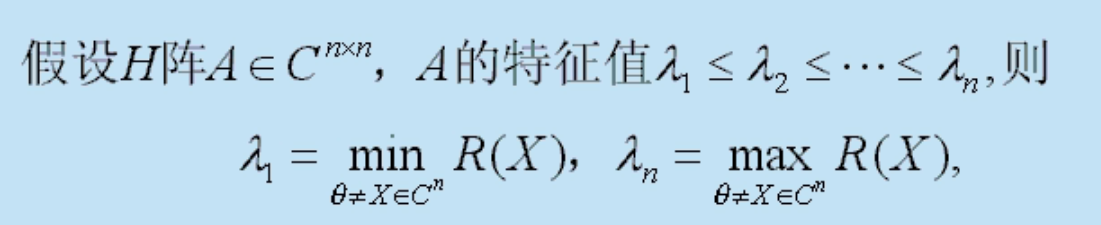
注意这里强调一定是\(Hermite\)阵,否则该定理不成立。


