第七讲 密钥管理技术
密钥管理的重要性
- 所有的密码技术都依赖于密钥。决定整个密码体制安全性的因素将是密钥的保密性。
- 在考虑密码系统的应用设计时,特别是在商用系统的设计时,需要解决的核心问题是密钥管理问题,而不是密码算法问题。
- 密钥的管理本身是一个很复杂的课题,而且是保证安全性的关键点。
密钥管理的目的和要求
密钥管理是一门综合性的技术,涉及密钥的产生、检验、分发、传递、保管、使用、销毁的全部过程,还与密钥的行政管理制度以及人员的素质密切相关。
密钥管理的目的
维持系统中各实体之间的密钥关系,以抗击各种可能的威胁:
- 密钥的泄露
- 秘密密钥或公开密钥的身份的真实性丧失
- 未经授权使用
密钥管理系统的要求
- 密钥难以被非法窃取
- 在一定条件下获取了以前的密钥用处也很小
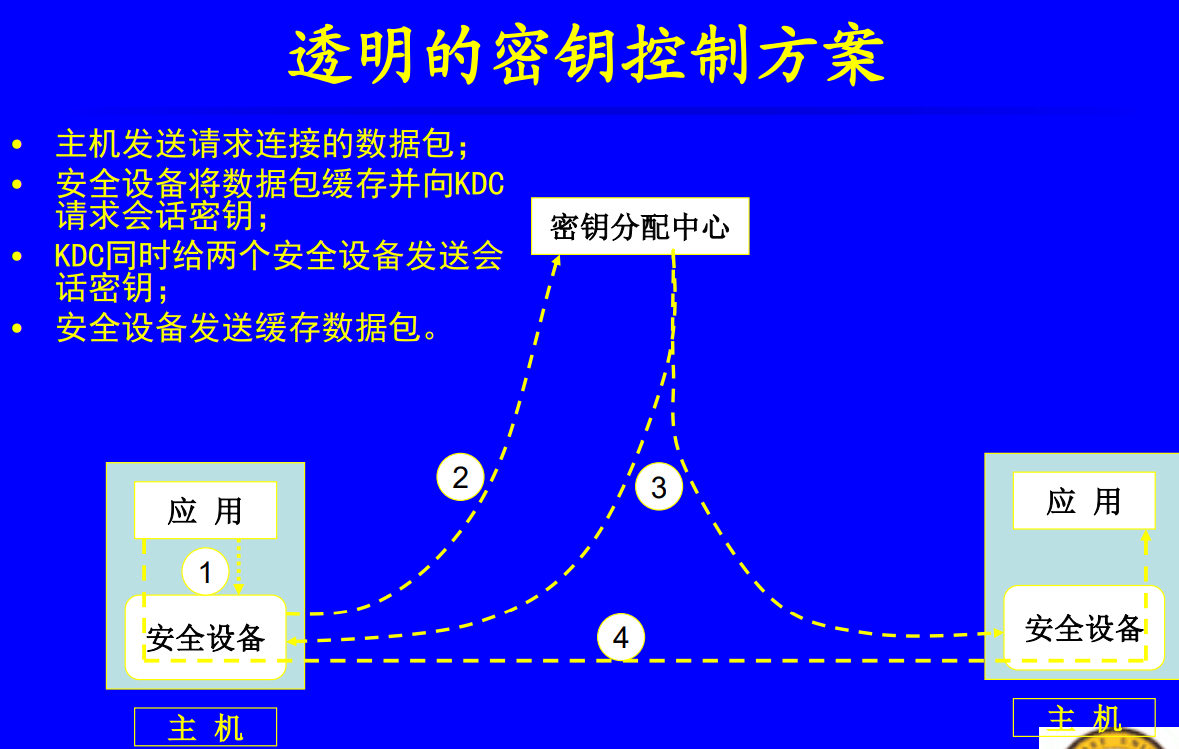
- 密钥的分配和更换过程对用户是透明的
密钥管理的原则
-
全程安全原则
必须在密钥的产生、存储、备份、分发、组织、使用、更新、终止和销毁等的全过程中对密钥采取妥善的安全管理。 -
最小权利原则
应当只分发给用户进行某一事物处理所需的最小的密钥集合 -
责任分离原则
一个密钥应当转职一种功能,不要让一个密钥兼任几种功能 -
密钥分级原则
可减少受保护的密钥的数量,又可简化密钥的管理工作。一般可将密钥划分为三级:主密钥,二级密钥,初级密钥。 -
密钥更新原则
密钥必须按时更新。否则,即使是采用很强的密码算法,使用时间越长,敌手截获的密文越多,破译密码的可能性就越大 -
密钥应当有足够的长度
密码安全的一个必要条件是密钥有足够的的长度。密钥越长,密钥空间就越大,攻击就越困难,因而也就越安全。 -
密码体制不同,密钥管理也不相同
由于传统密码体制与公开密钥密码体制是性质不同的两种密码,因此它们在密钥管理方面有很大的不同。
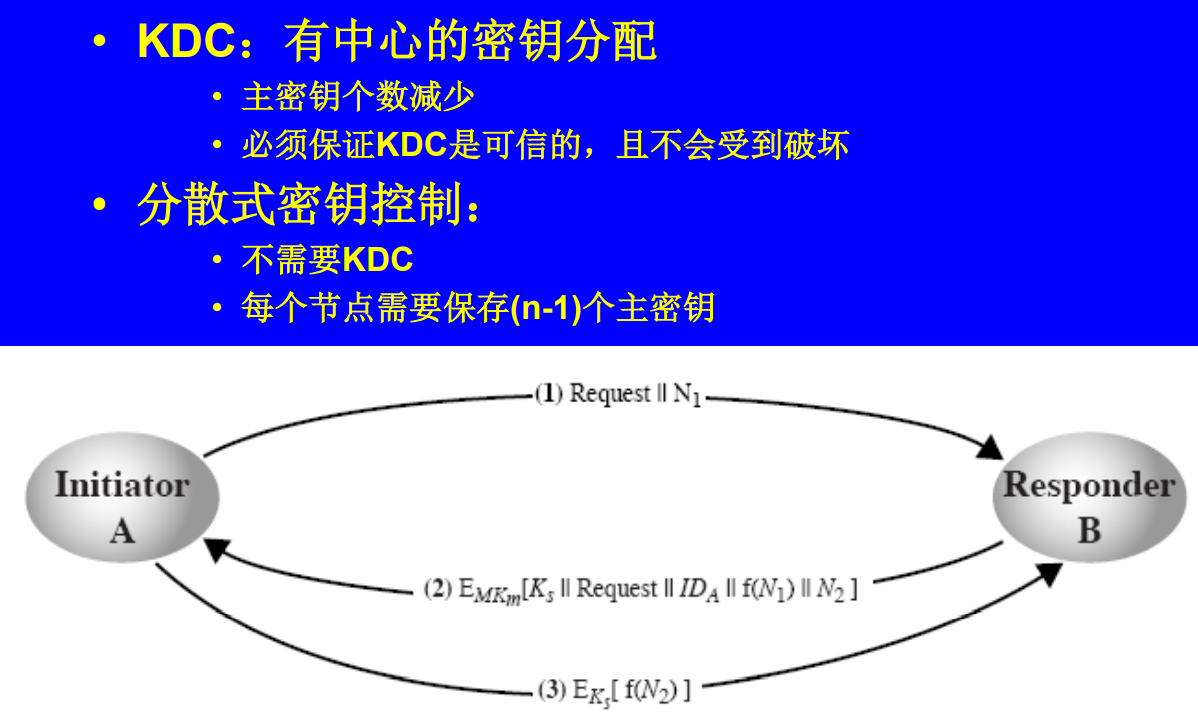
对称密钥管理技术
密钥分配
- 需求:
① 通信双方共享密钥,且不为他人所知
② 为保证通信安全,密钥必须经常变动 - 密钥分配方法:
① 密钥由A选择,并亲自交给B(人工)
② 第三方选择密钥吼亲自交给A和B(人工)
③ A或B使用最近使用过的密钥加密新密钥再发给另一方
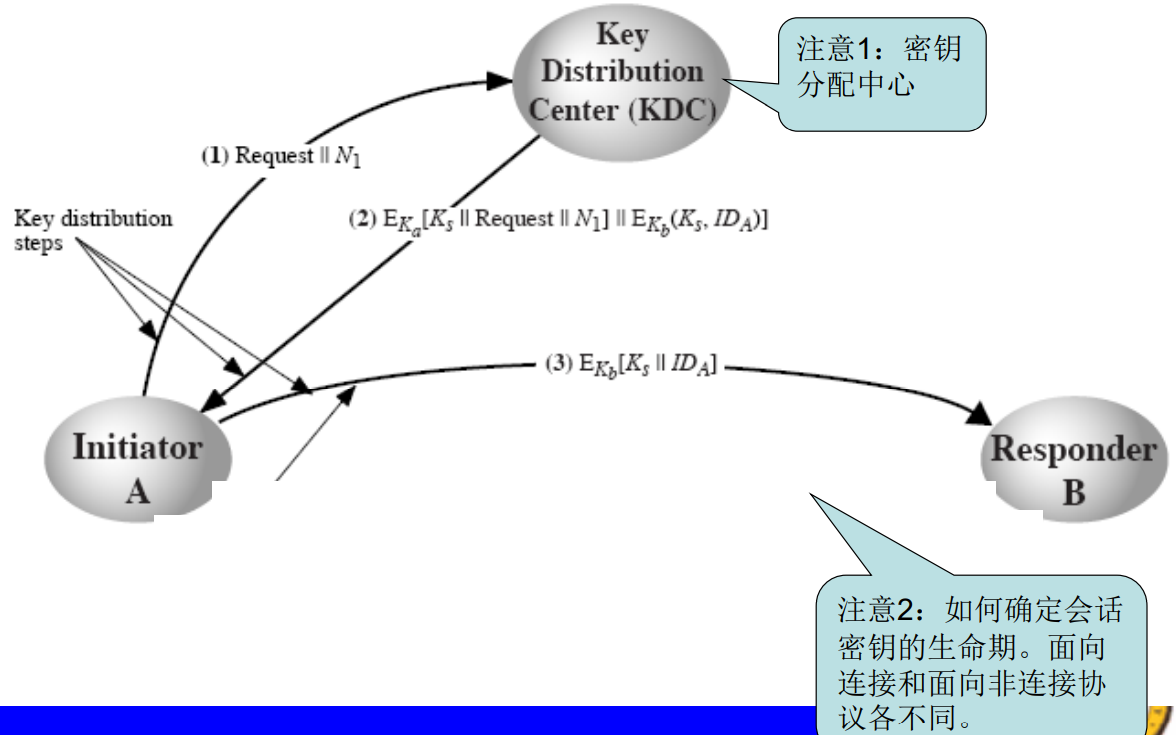
④ A和B与第三方C均有秘密通道,则C可将密钥分别秘密发给A和B - 典型的对称密钥分配模式:
密钥分配中心(KDC)负责分发密钥给需要的用户。
- 分散式密钥控制
- 其他密钥分配方案
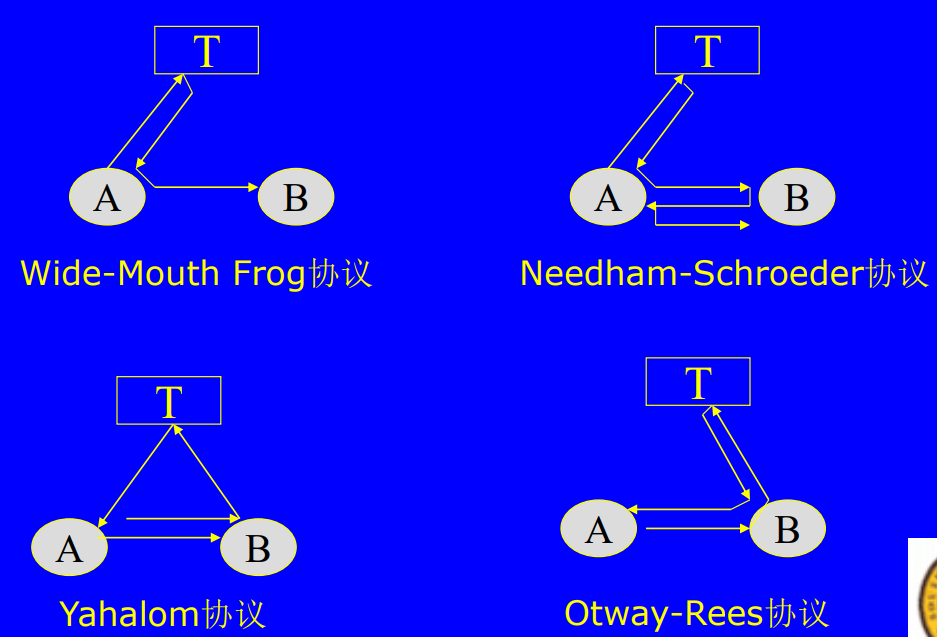
随机数的应用
- 密钥分配时的临时交互号nonce,防止重放攻击
- 会话密钥产生
- RSA公钥加密中密钥的产生
- 密文分组连接、密文反馈链接和输出反馈链接使用的IV
BBS发生器是现在产生安全伪随机数的普遍方法。它的安全性是基于大数分解的困难。
公钥密码的管理技术
- 密钥分配
① 公钥分配
② 公钥密码用于传统密码体制的密钥分配 - 公钥分配方法
① 公钥的公开发布
② 公钥可访问目录
③ 公钥授权
④ 公钥证书
公开发布
- 方法简便
- 缺乏安全性,任何人都可以伪造其他人的公钥

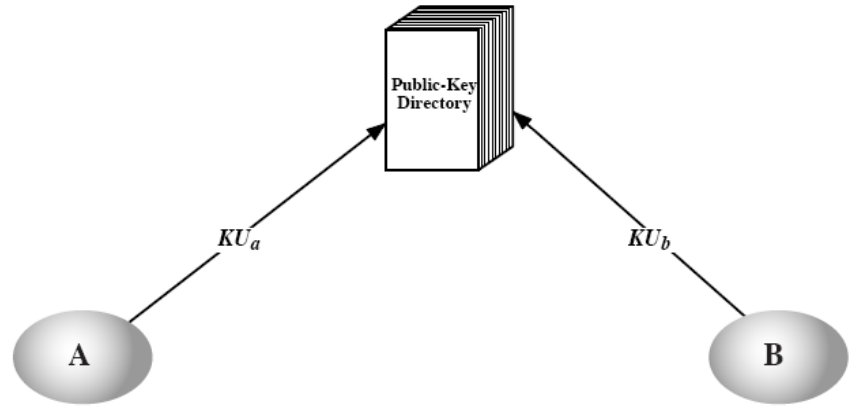
公开可访问目录
- 类似于电话号码簿
- 用户注册必须通过安全的认证通信
- 缺点:一旦攻击者获得管理员的私钥即可以传递伪造的公钥。
公钥授权
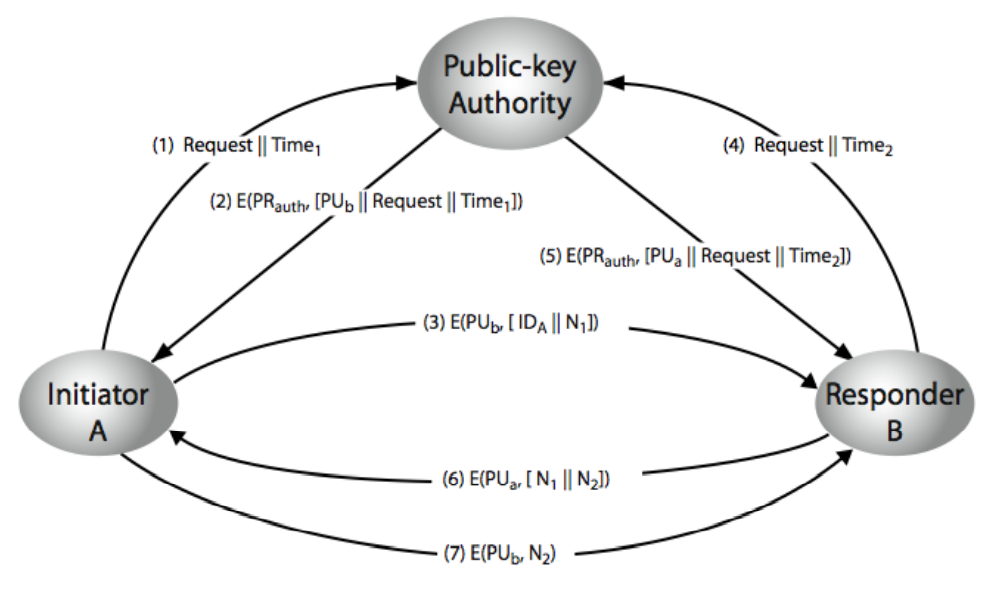
参数\(N_1\)用来防重放、验证身份,参数\(N_2\)只用来验证身份。
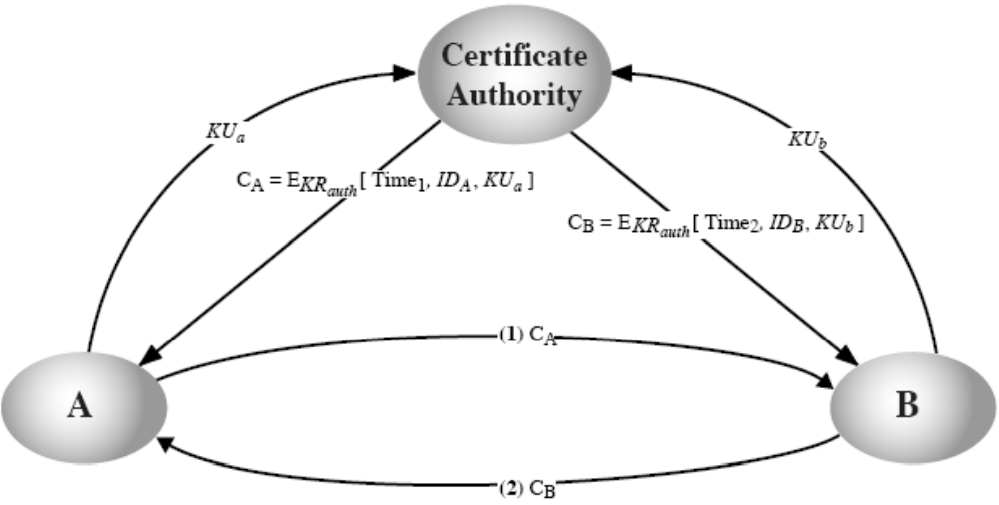
公钥证书
- 通信双方使用证书来交换密钥,而不是通过公钥管理员
- 证书包含用户编号和公钥,由证书管理员产生。
- \(C_A=E_{KRauth}[T,ID_A,K_{Ua}]\)
利用公钥密码分配传统密码体制的密钥
- 简单的密钥分配
- 具有保密性和真实性的密钥分配
- 混合方法
利用公钥密码分配主密钥
利用主密钥实现秘密的会话密钥分配
KDC与每一个用户分别共享一个秘密的主密钥
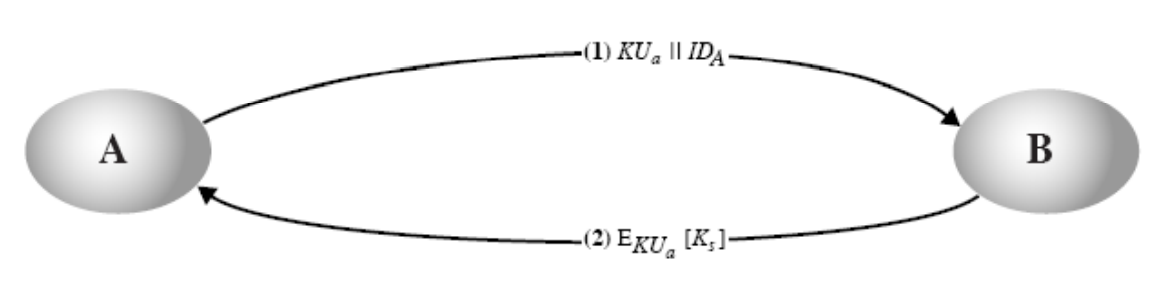
简单的密钥分配
- 协议简单
- 可以抗窃听攻击
- 容易受中间人攻击:重放截获的信息、对消息进行替换
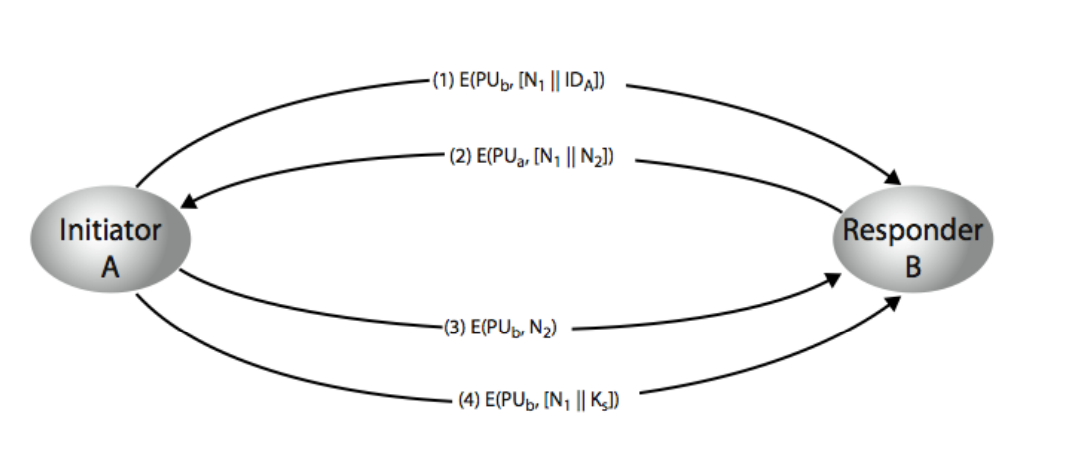
具有保密性和真实性的密钥分配方法
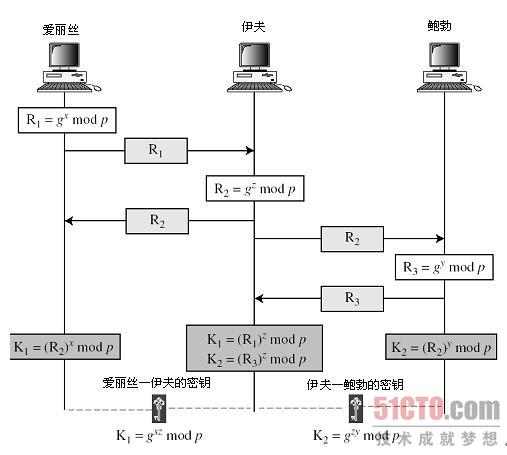
Diffie-Hellman密钥交换
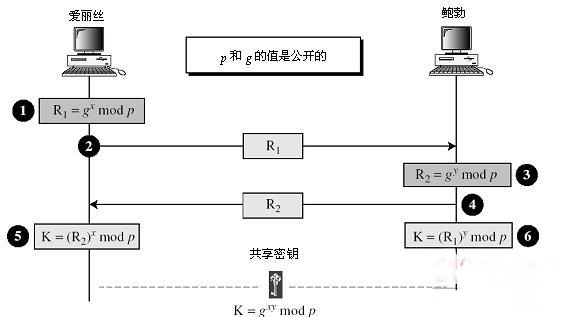
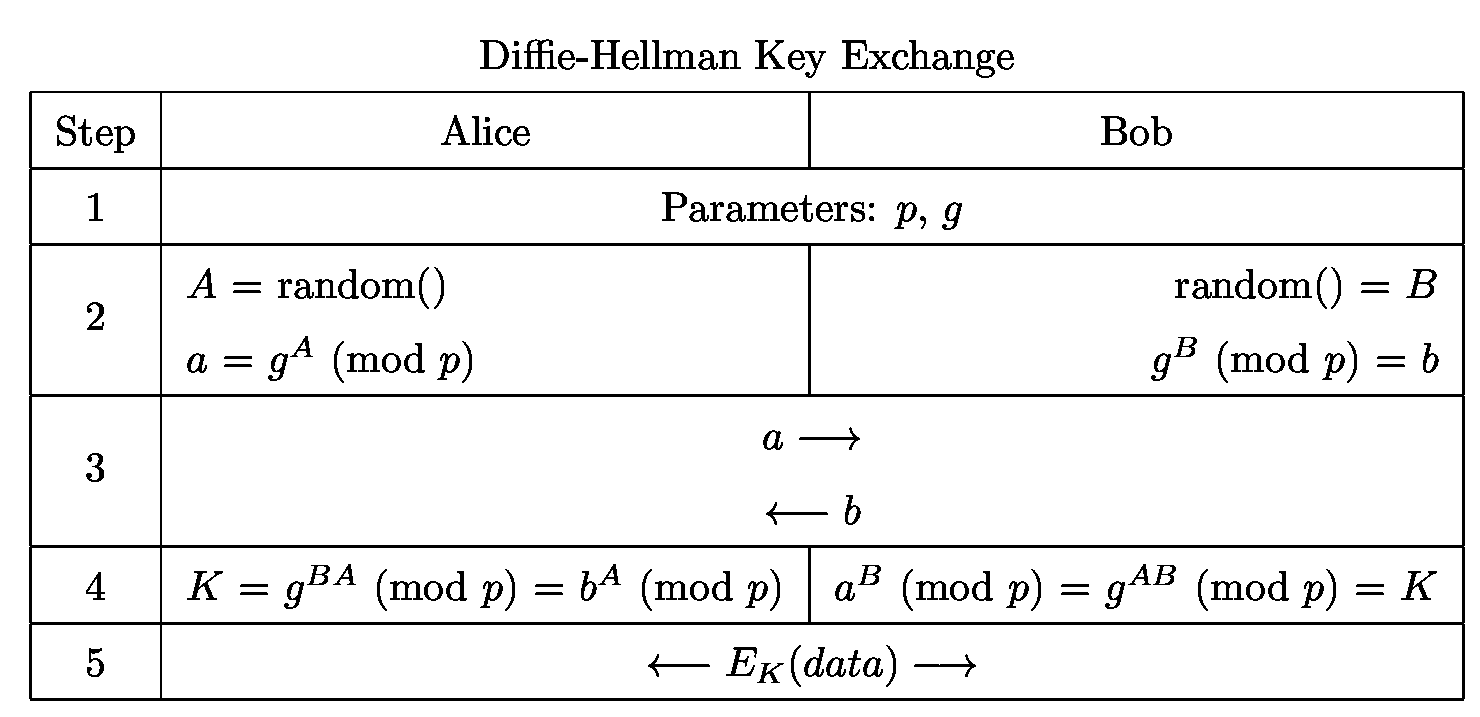
- 举例说明:

- 一个方便理解的图:
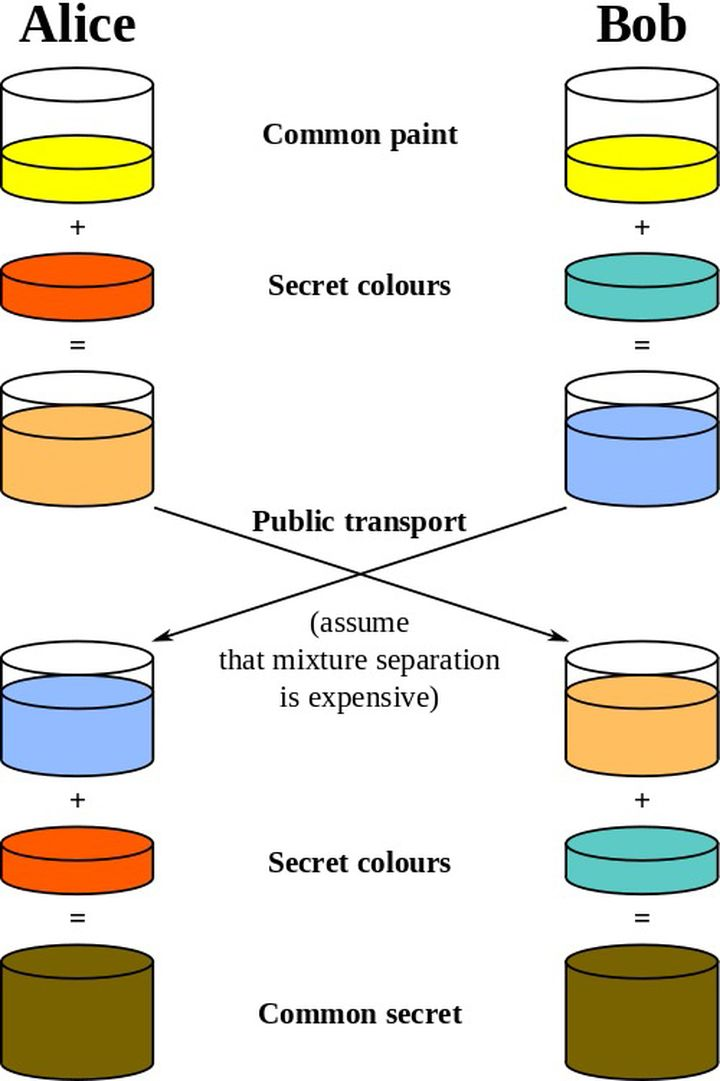
- 该算法仅能完成密钥交换,使得两个用户可以安全地交换密钥,用于后续的通讯过程,
- 算法的安全性建立在:
① 求关于素数的模素数幂运算相对容易
② 计算离散对数非常困难
③ 对于大素数,求离散对数被认为不可行 - 容易受到中间人攻击