第二讲 密码学的数学基础

群、环和域

• 群是两个元素作二元运算得到的一个新元素，需要满足群公理。
• 环在阿贝尔群（也叫交换群）的基础上，添加一种二元运算乘法 $·$（虽叫乘法，但不同于初等代数的乘法）。一个代数结构是环$(R, +, ·)$，需要满足环公理。
• 域在交换环的基础上，还增加了二元运算除法，要求元素（除零以外）可以作除法运算，即每个非零的元素都要有乘法逆元。

逆元的存在是为了解密。因此，密码学要以域为研究对象。

由此可见，域是一种可以进行加减乘除（除0以外）的代数结构，是数域与四则运算的推广。整数集合，不存在乘法逆元（$\frac{1}{3}$不是整数），所以整数集合不是域。有理数、实数、复数可以形成域，分别叫有理数域、实数域、复数域。

• 在密码学中为什么采用有限域？
  所有的加密算法都涉及整数集上的算术运算。如果某种算法使用的运算之一是除法，那么我们就必须使用定义在域上的运算。
  加密算法需要明文与密文一一映射关系，而密文是有限的，无限域存在浪费。
• 为什么采用模运算？
  模运算能够造出有限域（定义除法）

有限域和$GF(2^n)$的形式的有限域

有限域即含有有限个元素的域。
元素个数为$p^n$的有限域一般记为$GF(p^n)$。
运用$GF(2^n)$的原因是：加密运算要求将整数平均地映射到自身且构造的整数集合必须是一个域。

为了使资源不浪费，不使用直接的模运算而是使用既约多项式模运算。

• 为什么密码学采用$GF(2^n)$形式的有限域，而不采用$GF(p)$形式的有限域？
  为了方便实用和提高效率，希望这个整数集中的数与给定的二进制位数能够表达的信息一一对应而不出现浪费，即希望整数集的范围是$[0,2^n-1]$。

素数

素数（质数）是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。
任意正整数可由素数的乘积来表示。

同余会使得多个明文对应同一个密文（即二义性），虽更安全但失去了可用性。因而多数情况下选择对一个素数进行模运算。

Fermat定理和推论

定理

若$p$是素数，$m$是正整数且不能被$p$整数，则

$$m^{p-1}\equiv1\ mod\ p$$

推论

Fermat定理的另一种有用表示：若$p$是素数，$m$是任意正整数，则

$$m^p\equiv m\ mod\ p$$

理解为乘了一个$m$即可。

Euler函数

Euler函数$\phi(n)$，指小于$n$且与$n$互素的正整数的个数。

• 对于素数$p$有：

$$\phi(p)=p-1$$

• 由此，对于素数$p$和$q$，$p\neq q$，那么对$n=pq$，有：

$$\phi(n)=\phi(pq)=\phi(p)\ \phi(q)=(p-1)(q-1)$$

Euler定理和推论

定理

对于任意互素的$m$和$n$，有：

$$m^{\phi(n)} \equiv 1\ mod\ n$$

另一种有用表示：

$$m^{\phi(n)+1} \equiv m\ mod\ n$$

本质就是将Euler函数运用在Fermat定理上。

推论

给定两个素数$p$和$q$，整数$n=pq$，对于小于$n$的任意正整数$m\ (0<m<n)$，有以下关系式成立：

$$m^{\phi(n)+1} \equiv m^{(p-1)(q-1)+1} \equiv m\ mod\ n$$

另一种表达形式：

$$m^{k\phi(n)+1} \equiv m\ mod\ n$$

离散对数

本原根

如果使得$a^m\equiv 1\ mod\ n$成立的最小正幂$m$满足$m=\phi(n)$,则称$a$是$n$的本原根。 其中$\phi(n)$为欧拉函数。

• 若$a$是$n$的本原根，则$a$的$1$到$\phi(n)$次幂模$n$是各不相同的，且均与$n$互素。
• 若$p$为素数时，若$a$是$n$的本原根，则$a$的$1$到$(p-1)$次幂模$p$是各不相同的。
• 模$p$的本原根共有$\phi(p-1)$个

本质上讲本原根的意思就是该数的$1$到$n$次方逐个$mod\ n$，结果各不相同且均$∈[1,n-1]$。所以$n$的本原根应该就是指模$n$的本原根。
参考：密码学基础 本原根

• 示例
  

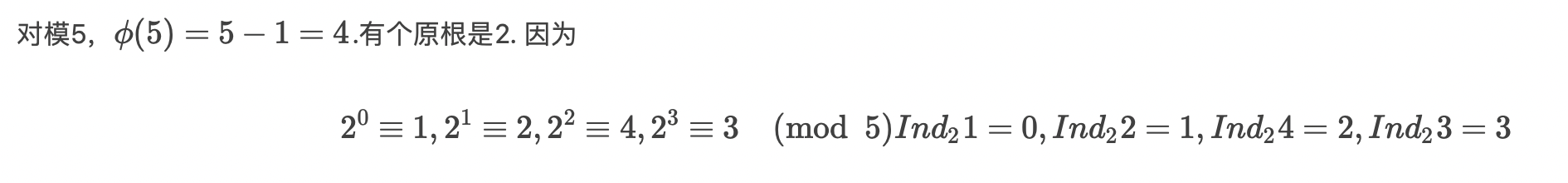
定义

对于某素数$p$，$p$的本原根为$a$；
对于任何整数$b$，$b\equiv r\ mod\ p$；
存在唯一的整数$i$，$0≤i≤(p-1)$，使得

$$b\equiv a^i\ mod\ p$$

$i$称为以$a$为底$b$的指标$ind_{a,p}(b)$，也记为离散对数，记为$dlog_{a,p}(b)$

性质

离散对数和一般的对数有着相类似的性质：

$$ind_xy≡ind_x+ind_y(mod\ ϕ(m))ind^y_x≡y\ ind_x(mod\ ϕ(m))$$

计算

$y\equiv g^x\ mod\ p$
已知$g，x，p$，计算$y$是容易的
已知$y，g，p$，计算$x$是容易的