2 内积空间与等距变换
线性空间的具体模型是三维几何空间,但是几何空间中的度量概念——向量的长度及向量间夹角在第1章的线性空间中还没有体现,而这种度量概念在有些问题中是需要的。本章中引进与几何空间中向量的数量积相对应的内积,在此基础上定义向量的长度、夹角,最后介绍几何空间中直角坐标变换相对应的等距变换。
内积与内积空间
若一个二元函数满足四条公理:
- 共轭对称性
- 齐次性
- 可加性
- 正定性
即,要判断一个复(实)线性空间的复(实)函数是否为内积,只要验证内积定义中的4条性质满足即可。
在欧氏空间中:\(<\alpha,\beta>=\beta^T \alpha\)
在酉空间中:\(<\alpha,\beta>=\beta^H \alpha\)
则该二元函数为内积,它所属的线性空间为内积空间。
特别地,当数域为实数域时为欧氏空间;数域为复数域时为酉空间。
在数域为复数域时,用共轭转置H来代替在实数域中的直接转置T是因为要保证结果为正数,而复数的平方会出现负数的情况,因此要取共轭。
- 要证明内积空间的非空子集是子空间,除利用子空间性质,还要证明保持内积性质。
长度与夹角
- \(Cauchy-Буняковский\)不等式
- 三角不等式
可以用向量和距离两种方式表示。 - 勾股定理
夹角的定义
\(cos \phi=\frac{<\alpha,\beta>}{||\alpha||·||\beta||}\),称\(\phi\)为\(\alpha\)与\(\beta\)的夹角
- 若\(<\alpha,\beta>=0\),则称向量\(\alpha\)与\(\beta\)正交,记为\(\alpha ⊥ \beta\).
距离的定义
称\(d(\alpha,\beta)=||\alpha-\beta||\),为\(\alpha\)与\(\beta\)的距离。
正交基与Schmidt正交化
正交向量组与正交基的定义
由两两正交的非零向量组成的向量组称为正交向量组
由两两正交的单位向量组成的向量组称为标准正交向量组
作为正交向量组的基称为正交基
作为标准正交向量组的基称为标准正交基
由此,在标准正交基下的度量矩阵是单位矩阵。
Schmidt正交化方法
正交化+单位化→标准正交基
※ 注意:标准正交基不唯一。
这里可以结合度量矩阵来计算正交化过程中每一项之前的系数。
- 例题:
假设\(V\)在基\(\epsilon_1,\epsilon_2\)下的度量矩阵是\(A=\begin{pmatrix}1&2\\2&5\end{pmatrix}\),求\(V\)的一组标准正交基。
解:
- 正交化:\(\beta_1=\epsilon_1\)
\(\beta_2=\epsilon_2-\frac{<\epsilon_2,\beta_1>}{<\beta_1,\beta_1>}\beta_1\)=\(\epsilon_2-\frac{1}{2}\epsilon_1\)=\(\epsilon_2-2\epsilon_1\)
注意这里代入了度量矩阵的\((1,1)\)和\((2,1)\)两项。
定义\(\alpha=\begin{pmatrix}-2\\1\end{pmatrix}\),用于之后单位化。
- 单位化:\(r_1=\frac{1}{||\beta_1||}\beta_1=\epsilon_1\)
\(r_2=\frac{1}{||\beta_2||}\beta_2=\frac{1}{\sqrt{<\beta_2,\beta_2>}}\beta_2=\beta_2=\epsilon_2-2\epsilon_1\),其中\(<\beta_2,\beta_2>=\alpha^TA\alpha=\begin{pmatrix}-2&1\end{pmatrix}\begin{pmatrix}1&2\\2&5\end{pmatrix}\begin{pmatrix}-2\\1\end{pmatrix}=1\)
这里“其中”后的内容很重要,结合度量矩阵简化了运算。
- \(V=R_3[x]\)(数域\(R\)上次数小于3的全体多项式及零多项式)默认的基为\(1,x,x^2\),可以直接使用。
标准正交基的扩张定理
同普通的基一样,标准正交基也存在扩张定理。
假设\(W\)是\(V\)的子空间,那么\(W\)的一组标准正交基可以结合其他几个向量扩充为\(V\)的标准正交基。
度量矩阵
一组基的度量矩阵有如下性质:
- 度量矩阵是正定的
- 不同基的度量矩阵是合同的
度量矩阵的本质就是基中各向量的内积的结果。
酉矩阵
若\(A^HA=I\),则称n阶复矩阵A为酉矩阵。
且同时满足,\(A\)是酉矩阵\(\leftrightarrows A^HA=I \leftrightarrows A^{-1}=A^H\leftrightarrows A\)的行(列)向量组是\(C^n\)的标准正交基。
酉矩阵其实就是在复数域内的正交矩阵。
可逆阵的UT分解
设\(A\)为\(n\)阶可逆阵,则存在酉阵\(U\)即主对角元恒正的上三角阵\(T\),使
且这种分解唯一。
正交子空间
- 若要证明一个向量与线性空间正交,只需要证明这个向量与该线性空间的每一生成元都正交。
这里的生成元指的是生成子空间中的生成向量组的概念。(可以把生成元理解为基)。
详情可以看上一章的笔记。
正交补空间
- 设\(W≤V\),记
易证这是\(V\)的子空间,称是\(V\)的正交补空间。
- 定理:若\(W≤V\),则\(V=W\oplus W^⊥\),且该正交补空间唯一。
- 推论:若\(W≤V\),则\((W^⊥)^⊥=W\)
正交补空间的应用
- \([R(A)]^⊥=K(A^H)\)、\([K(A)]^⊥=R(A^H)\)
- 正投影(最佳逼近)和最短距离
设W是内积空间V的有限维子空间,则对V中任一向量\(\alpha\)必存在唯一\(\beta ∈W\),使\(d(\beta,\alpha)=\mathop{min}\limits_{\zeta ∈W} d(\zeta,\alpha)\leftrightarrows (\beta-\alpha)⊥W\),称如上\(\beta\)为\(\alpha\)在子空间\(W\)上的正投影,也叫\(\beta\)是\(\alpha\)在子空间\(W\)上的最佳逼近,\(||\beta - \alpha||\)为\(\alpha\)到\(W\)的最短距离。
求正投影的示例:

本质其实就是使得 差向量 对于线性空间的每一个 生成元 都正交。
- 内积空间正交直和分解
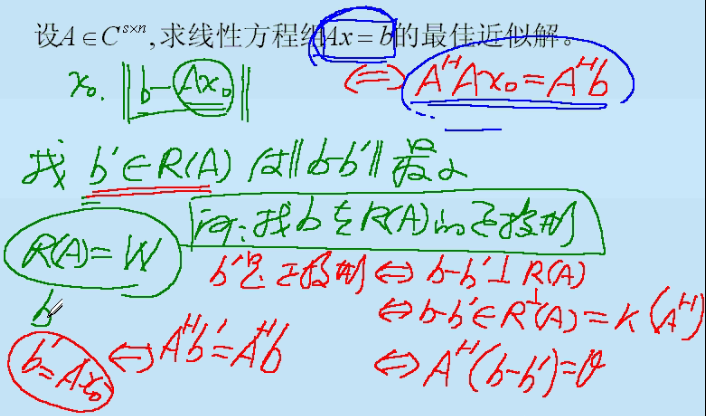
两个正交子空间下的向量与其对应的正投影正交,即互为正交投影,同样地,差向量的模也被称为\(\alpha\)到\(W\)的最短距离。 - 最小二乘解
可以用来求线性方程组的最佳近似解。
等距变换
等距变换就是内积空间中保持内积不变的线性变换。特别地,当\(V\)是酉空间时,称为酉变换;当\(V\)是欧氏空间时,称为正交变换。
对于等距变换\(f\),以下四个条件等价:
- 保持长度不变
- 保持内积不变
- 将标准正交基变为标准正交基
- 在标准正交基下的矩阵是酉矩阵
证明内积空间的线性变换\(T\)是等距变换,只要证明\(T\)保持内积不变,或者证明\(T\)将标准正交基变成标准正交基。
备注:\(<f(x),f(y)>+<f(y),f(x)>=2Re<f(x),f(y)>\),这里的\(Re\)表示取实部的意思。
- 示例:

注意这里的内积其实可以当做一个数来看待,因此可以直接提出去。且单位向量的内积为1.
这个例子其实就是镜像变换。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号