1 线性空间与线性变换
关联:0 复习与引申
线性空间与线性变换是线性代数中最基本的两个概念,它们分别是\(n\)维向量空间\(F^n\)与线性变换\(Y=AX\)的推广。
线性空间证明
- 若要证明\(V\)是数域\(P\)上的线性空间(表示为\(V(P)\),必须验证\(V\)对于向量的加法与数乘运算封闭,且满足8条性质;
- 若要说明\(V\)不是数域\(P\)上的线性空间,则只需说明\(V\)对于向量的加法与数乘运算其中之一不封闭,或者运算不满足8条中的某一条即可。
线性空间的性质:
线性表示
- 以少表多,多的相关。
基和维数
- 基和维数本质上很像极大无关组和秩(亦或是基础解系)
- 线性空间的基不一定存在
求基和维数的一些例题:
- 如题:在数域中,均为n维向量,那就让每一位分别为1(就像构筑坐标轴那样),于是维数就是n,基就是分别为1其余为0的各个n维向量
- 如题:在数据中,均为\(2*2\)矩阵,依然是让每一位分别为1的思路,如\(E_{11}\)、\(E_{12}\)、\(E_{21}\)、\(E_{22}\)即可构筑一个基,进而得到维数为4
由此可以类推到\(s*n\)阶的矩阵情况下。
求维数
- 要说明一个线性空间\(V\)的维数是n,只需找出\(V\)中n个线性无关的向量,并且\(V\)中每一个向量均可以由这n个向量线性表示。
坐标与基
坐标要与基在一起才有意义。
- 这里注意坐标的表示形式:

最后要把a、b、c、d竖起来作为坐标结果。
求基和维数
- 一维的情况:
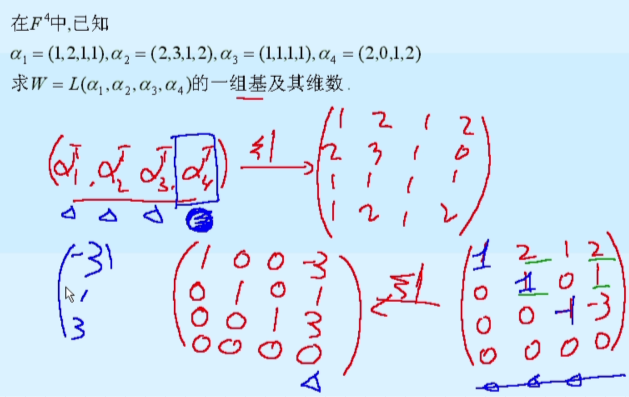
- 二维的情况:

核心思想其实就是这样竖起来,变成坐标,然后行初等变换就可以求基了。
向量组的线性相关性
- 一道例题:

过渡矩阵

- 过渡矩阵的用途:

注意这里由\(e\)到\(α\)是经过过渡矩阵\(A\),所以有\(α\)到\(e\)就需要经过过渡矩阵\(A\)的逆,然后由\(e\)再到\(β\)经过过渡矩阵\(B\),这样即可达成从\(α\)到\(e\)再到\(β\)的串联,即\(A^{-1}B\)。
由此引出了下面的坐标变换公式。
- 坐标变换公式:


子空间证明
要证明\(W\)是\(V\)的子空间,首先说明\(W\)不空,再证明\(W\)对\(V\)的两种运算封闭即可。
- 平凡子空间:
零空间 \({θ}\) 和 \(V\) 空间本身都是 \(V\) 的子空间,又被叫做平凡子空间。
从几何的角度理解:若空间构成的平面或直线经过原点,则它构成子空间,否则由于不封闭,无法构成子空间。
生成子空间
- 设一个线性空间\(V\)中的向量组,则该向量组所有可能的线性组合所构成的集合是\(V\)的生成子空间,称为\(V\)的生成子空间;称对应的向量组为生成向量组,简称生成组。
- 生成向量组的极大线性无关组是生成子空间的基,故 \(dim\)(生成子空间)=\(rank\)(生成向量组的秩)
因此求生成子空间的基和维数,就等价于求该生成子空间向量组的极大线性无关组和秩(即,极大线性无关组向量的个数)。
基扩张定理
线性空间中一组线性无关的向量可以结合其余向量构成该线性空间的基。
求两个子空间交于和的基与维数
知道基自然也就知道维数了。
-
和的基与维数
\(V_1\)+\(V_2\)的基和维数比较好求,直接拼起来求极大无关组就可以。 -
交的基与维数
- 求出使\(\xi=x_1 \alpha_1+x_2 \alpha_2+…+x_r \alpha_r=y_1 \beta_1+y_2 \beta_2+…+y_s \beta_s\) 的极大无关组\(\xi_1,\xi_2,…,\xi_k\),就是\(V_1∩V_2\)的基。
- 求\(V_1∩V_2\)的维数可以用维数定理:\(dimV_1+dimV_2=dim(V_1+V_2)+dim(V_1∩V_2)\)
也就是可以通过求和的维数来迂回的求交的维数。
直和
证明 \(W=W_1 \oplus W_2\):首先证明\(W=W_1+W_2\),其次证明\(W_1∩W_2=\left\{0\right\}\) 或者 \(dimW=dimW_1+dimW_2\)。

并集(和)线性无关即为直和;
可以简单的理解为:交为空,并为全。
线性映射
- 双射才是可逆的
dimV有限时,f ∈ Hom(V,V),则\(f\)可逆\(\leftrightarrows\)\(f\)是单射\(\leftrightarrows\)\(f\)是满射
- 齐性+可加性→线性映射,线性空间到线性空间自身的映射称为线性变换,记\(V(F)\)到\(U(F)\)的一切线性映射之集合为\(Hom(V,U)\)
- 线性映射的性质:

理解映射时可以把映射理解为矩阵,在计算等很多方面也很类似(关联到线性映射的矩阵)。
这里比较重要的就是值域和核的概念。
线性变换的运算
线性变换的运算包括数乘和求和。
- 线性变换的运算的性质:
- \((fg)h=f(gh)\)
- \(f(g+h)=fg+fh\)
- \((g+h)f=gf+hf\)
注意乘法不满足交换律。
线性映射的矩阵

这里就和相似矩阵的定义相关联。
- 例题:

- 定理:

也就是说求线性变换在一组基下的矩阵有两种求法:①直接求法和②间接求法,间接求法指的就是这里的\(B=P^{-1}AP\)
值域与核
\(dimR(f)+dimK(f)=dimV\),即值域的维数+核的维数=线性变换的维数。
-
定理:
假设\(f∈Hom(V,U)\),则
\(f\)是满射\(\leftrightarrows R(f)=U\)
\(f\)是单射\(\leftrightarrows K(f)=\left\{\theta \right\}\) -
求值域和核的基与维数(知道基就知道维数了):
设\(T\)在基\(\alpha_1,\alpha_2,…,\alpha_n\)下的矩阵是\(A\)
- 求出矩阵\(A\)的极大无关组,再与基\(\alpha_1,\alpha_2,…,\alpha_n\)相乘即可得到值域\(R(T)\)的一组基;
- 求出齐次线性方程组\(AX=0\)的基础解系,再与\(\alpha_1,\alpha_2,…,\alpha_n\)相乘即可得到核\(Ker(T)\)的一组基
核心在于求出线性变换在基下的矩阵,然后将矩阵通过初等行变换化为行最简型,将 极大无关组/基础解系 与 基 相乘即可得到对应的结果。
不变子空间
值域和核均为不变子空间,且刚好可以作为一个线性空间的直和分解。
引入不变子空间是为了简化线性映射的矩阵的表示形式。因而较为重要的部分就是将线性空间分解为两个不变子空间的直和,然后就可以简化矩阵的表示。(常拆成值域和核)
几何空间线性变换的例子
- 辑射相似变换
- 平行于某矢量的投影变换
- 平行于某一方向的压缩(或延伸)
- 平行于某方向的推移
线性空间的同构
双射+线性映射→线性空间同构、该映射为同构映射
- 充要条件
数域\(F\)上两个有限维线性空间\(V\)与\(U\)同构的充分必要条件为\(dimV=dimU\)


