深入浅出地讲解RSA密码

起因是恰好最近正在学密码学相关的内容，然后看到知乎有梳理的很不错的文章，就想看来自己再总结一下。

1 对称加密与非对称加密

首先，RSA是典型的非对称加密算法。这里就需要与传统的对称加密进行区分。

从前有个女孩叫做Alice，她想告诉Bob一个秘密。然而有个叫Eve的人想要偷听。所以Alice需要想办法加密这条信息，防止Eve偷听。

古典的思路是：Alice和Bob提前准备了一个盒子，并配了两把钥匙。每次Alice把秘密装进盒子里，然后用钥匙锁起来寄给Bob。Bob接到盒子后用钥匙打开，便可以知道这个秘密了。(这里的钥匙其实是将加密秘钥求逆得出的解密秘钥，但可以直接由加密秘钥推导出解密秘钥，故可以理解为同一把钥匙。)加密秘钥和解密秘钥相同，或实质上等同，即从一个易于推出另一个。

这种方式叫做对称加密，又称传统密码算法、秘密密钥算法或单密钥算法。

其中，这个秘密本身叫做明文，用来加密的钥匙叫做密钥，锁好了的信息叫做密文。

Alice和Bob都有密钥，所以他们都可以随意地把明文翻译成密文，或是把密文翻译成明文。但Eve没有密钥，所以无法破解密文。

然而，在现代网络的实际应用中，这种对称加密却有很多很多的问题！其中，最大的问题是：很多情况下，Alice和Bob可能没有机会提前商量，所以无法生成相同密钥！然而如果进行秘钥商讨，或对密钥进行直接传输，将会有可能泄露密钥。

所以我们需要更好的办法，就是——非对称加密。RSA是就是非对称加密。一般的钥匙都是既能上锁、也能开锁的。但是，非对称加密中，密钥有两种：公有密钥、私有秘钥。

公有密钥用于上锁（加密）,其他人都可以知道。私有密钥用于解锁（解密），只能自己知道。

因为Alice只需要上锁，所以她只需要公有密匙就够了。私有密匙只有Bob拥有。

Alice会先通知Bob：我要告诉你一件事。然后Bob接着就会生成一把锁，并制作两种钥匙：公有密钥和私有秘钥。Bob会把公有密钥发给Alice，然后Alice会用公有密钥加密信息。Alice把上锁的密文发回来后，Bob再用自己的私有密钥解密，并得到明文。
整个过程中，只有Bob拥有私有密钥。
Bob的私有秘钥不会交给任何人的。
纵使Eve获得了明文和公开密钥，Eve也无法解密。因为只有私有密匙才可以解密。

非对称加密的基本原理就是这样。
这种加密方式的好处就是在加密解密信息的同时，还可以进行签名和验证（只需要将私钥用来签名，公钥进行验证即可）。
为了打造这两把钥匙，一把用于上锁，一把用于开锁，我们还需要利用一些数论方面的知识。

这里略过了对于相关算法时间复杂度的讲解，只需要知道在密码学中，很多时候密码不是不可以破解的，只不过破解密码需要大量的时间。 当破解密码所要耗费的成本大于其收益时，我们就可以认为这个加密算法是绝对安全的，这也就是为什么随着加密算法和计算能力在不断的相互促进中共同发展。

而目前RSA理论上非常安全，因为破解RSA所要付出地计算成本远远高于使用RSA进行加密的计算成本。
（对于RSA来说，目前最大的威胁是量子计算机的快速发展，当然也会有相应的量子加密产生就是了。）

2 数论

2.1 欧拉函数——φ()

φ(n)表示：小于n的正整数中与n互质的数的数目。（互质表示公因数为1）

比如想要知道φ(10)的话，我们就可以看[1, 10)中和10互质的整数，也就是1、3、7、9这四个数。（2、4、6、8和10有公因数2，而5和10有公因数10）。所以φ(10)=4。

比如想要知道φ(21)的话，我们就可以看[1, 21)中和21互质的整数，也就是1、2、4、5、8、10、11、13、16、17、19、20这12个数。（3、6、9、12、15、18和21有公因数3，而7、14和21有公因数7）。所以φ(21)=12。

如果n能写作两个不同质数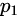与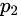的乘积，那么

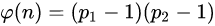
比如10=2*5，2和5是两个质数，所以φ(10)=(2-1)*(5-1)=4。
比如21=3*7，3和7是两个质数，所以φ(21)=(3-1)*(7-1)=12。

2.2 同余式

比如说，23÷7=3……2
再比如，65÷7=9……2

我们发现，这两个数除以7都余2，于是我们就可以这样写：

23 ≡ 65（mod 7）

当然也可以这样：

23 ≡ 2（mod 7）
65 ≡ 2（mod 7）

准确地说，如果a=b+km的话，a ≡ b（mod m）

同余式有这样两个性质：

同余式可以互相加：若a ≡ b（mod m）、c ≡ d（mod m），则a+c ≡ b+d（mod m）
同余式可以互相乘：若a ≡ b（mod m）、c ≡ d（mod m），则ac ≡ bd（mod m）

具体怎么用呢，举个例子：
既然我们知道23×(23+65)≡ 2×(2+2) ≡ 8 ≡ 1（mod 7）
因为23×(23+65) =2024，也就是说2024÷7余数是1。

2.3 欧拉公式

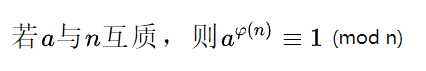
2.4 乘法逆元

如果ab ≡ 1（mod m），则称a和b为关于m互为乘法逆元。
已知a求b的方法：因为ab ≡ 1（mod m），所以不妨设ab+mk=1，其中a和m为已知数。
可以利用扩展欧几里得算法，可以在多项式时间内，计算出来一个乘法逆元b。
(事实上，b的解不唯一，这里只是求出了一个b。之前对称加密中，根据加密秘钥求解密秘钥的过程其实就是利用了乘法逆元。)

3 生成密钥对

我们终于开始构造咱们需要的两把钥匙了。

第一把：公钥，用于加密，送给Alice。

第二把：密钥，用于解密，Bob自己留好。

对于一个与n互质的数a：

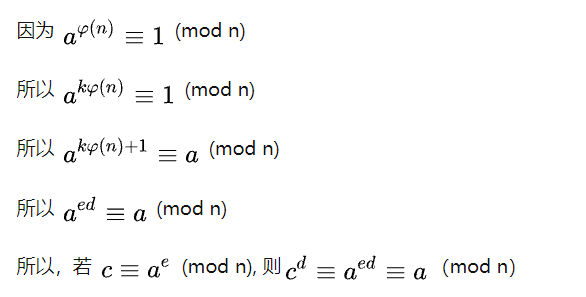
到这里，两把钥匙构造完成！

公钥：（n, e）

私钥：（n, d）

于是，对于明文a，Alice利用公钥（n, e）就可以加密为密文c了。

除了Bob，没有任何人可以知道φ(n)，所以没有人可以求出e关于φ(n)的乘法逆元d。
也就是说d的值从头到尾只有Bob自己知道，不可能泄露。
现在，Bob需要做的，仅仅是把公钥(n, e)交给Alice，让Alice把密文a加密成c，得到密文c后再用自己的密钥解密。
Eve就不可能窃听了。

个人理解： 整个RSA算法的核心其实就在于欧拉公式，将mod n 与 求乘法逆元d的过程巧妙的结合却又相隔开来，做到了在暴露n的情况下无法推出计算解密秘钥需要的φ(n)。
即，依靠φ(n)产生的ed互为乘法逆元，同时又可以靠产生φ(n)的n构建同余等式完成加解密，同时保证不可以靠n推出φ(n)，从而使得RSA算法十分安全。

参考:知乎