C++动态规划实现查找最长公共子序列
问题描述:
给定两个序列X={x1,x2,…,xm}和Y={y1,y2,…,yn},找出X和Y的最长公共子序列。(给定两个序列X和Y,当另一序列Z既是X的子序列又是Y的子序列时,称Z是序列X和Y的公共子序列。)
细节须知(与之前随笔的对比):
将由数组存储起来一并输出至文件修改为边运行边输出,增加了程序的鲁棒性。
算法原理:
a.最长公共子序列的结构
对X的所有子序列,检查它是否也是Y的子序列,从而确定它是否为X和Y的公共子序列。并且在检查过程中记录最长的公共子序列。X的所有子序列都检查过后即可求出X和Y的最长公共子序列。X的每个子序列相应于下标集{1,2,…,m}的一个子集。
b.子问题的递归结构
要找出X和Y的最长公共子序列,可按以下方式递归计算:当xm=yn时,找出Xm-1和Yn-1的最长公共子序列,然后在其尾部加上xm(=yn)即可得到X和Y的最长公共子序列。当xm≠yn时,必须解两个子问题,即找出Xm-1和Y的一个最长公共子序列及X和Yn-1的一个最长公共子序列。这两个公共子序列中较长者即为X和Y的最长公共子序列。
c.计算最优值
利用动态规划算法自底向上地计算最优值。
d.构造最长公共子序列
首先从b[m][n]开始,依其值在数组b中搜索。当b[i][j]=1时,表示Xi和Yj的最长公共子序列
1 #include<cstdio> 2 #include<cstring> 3 #include<stack> 4 #include<ctime> 5 #include<iostream> 6 #include<fstream> 7 #include<algorithm> 8 #include<windows.h> 9 using namespace std; 10 LARGE_INTEGER nFreq;//LARGE_INTEGER在64位系统中是LONGLONG,在32位系统中是高低两个32位的LONG,在windows.h中通过预编译宏作定义 11 LARGE_INTEGER nBeginTime;//记录开始时的计数器的值 12 LARGE_INTEGER nEndTime;//记录停止时的计数器的值 13 #define N 10000 14 //const int SIZE_CHAR = 10000; //生成32 + 1位C Style字符串 15 const char CCH[] = "_0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ_"; 16 int dp[N][N]; 17 char c; 18 int main(void) 19 { 20 //char a[N]; 21 //char b[N]; 22 //char a[SIZE_CHAR+2]; 23 //char b[SIZE_CHAR+2]; 24 ofstream fout; 25 int m = 0,i = 0; 26 int SIZE_CHAR; 27 cout<<"Please enter the number of times you want to run the program:"; //输入程序运行次数 28 cin>>m; 29 //int SIZE[m]; 30 double cost; 31 //double runtime[m]; 32 srand((unsigned)time(NULL)); 33 fout.open("data.txt",ios::app); 34 if(!fout){ 35 cerr<<"Can not open file 'data.txt' "<<endl; 36 return -1; 37 } 38 fout.setf(ios_base::fixed,ios_base::floatfield); //防止输出的数字使用科学计数法 39 for(i = 0; i < m; i++){ 40 //SIZE_CHAR=10000+RAND_MAX*(rand()%300)+rand(); //RAND_MAX=32767,随机生成数据量 41 SIZE_CHAR = rand() % 10000; 42 fout<<SIZE_CHAR<<","; 43 // SIZE[i]=SIZE_CHAR; //限定数据规模为10000~9872867 44 char a[SIZE_CHAR + 1] = {'\0'}; 45 char b[SIZE_CHAR + 1] = {'\0'}; 46 cout<<"☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆The "<<i+1<<"th test's string size is:"<<SIZE_CHAR<<"☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆"<<endl; 47 for (int i = 0; i < SIZE_CHAR; ++i){ 48 int x = rand() / (RAND_MAX / (sizeof(CCH) - 1)); 49 a[i] = CCH[x]; 50 } 51 cout<<"The first random sting is:" <<a <<endl; 52 for (int i = 0; i < SIZE_CHAR; ++i){ 53 int x = rand() / (RAND_MAX / (sizeof(CCH) - 1)); 54 b[i] = CCH[x]; 55 } 56 cout<<"The second random string is:" <<b <<endl; 57 cout<<"The longest common subsequence is:"; 58 QueryPerformanceFrequency(&nFreq);//获取系统时钟频率 59 QueryPerformanceCounter(&nBeginTime);//获取开始时刻计数值 60 int la=strlen(a); 61 int lb=strlen(b); 62 memset(dp,0,sizeof(dp)); 63 for(int i=1; i<=la; i++){ 64 for(int j=1; j<=lb; j++){ 65 if(a[i-1]==b[j-1]) 66 dp[i][j]=dp[i-1][j-1]+1; 67 else 68 dp[i][j]=max(dp[i-1][j],dp[i][j-1]); 69 } 70 } 71 int i=la,j=lb; 72 stack<char>s; 73 while(dp[i][j]){ 74 if(dp[i][j]==dp[i-1][j]){//来自于左方向 75 i--; 76 } 77 else if(dp[i][j]==dp[i][j-1]){//来自于上方向 78 j--; 79 } 80 else if(dp[i][j]>dp[i-1][j-1]){//来自于左上方向 81 i--; 82 j--; 83 s.push(a[i]); //压栈以便倒序输出 84 } 85 } 86 while(!s.empty()) 87 { 88 c=s.top(); 89 printf("%c",c); 90 s.pop(); 91 } 92 cout<<endl; 93 QueryPerformanceCounter(&nEndTime);//获取停止时刻计数值 94 cost=(double)(nEndTime.QuadPart - nBeginTime.QuadPart) / (double)nFreq.QuadPart; 95 fout<<cost<<endl; 96 //runtime[i]=cost; 97 cout<<"The running time is:"<<cost<<" s"<<endl; 98 } 99 fout.close(); 100 cout<<"Success!"<<endl; 101 return 0; 102 }
程序设计思路:
设序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}的最长公共子序列为Z={z1,z2,…,zk},则
a.若xm=yn,则zk=xm=yn,且Zk-1是Xm-1和Yn-1的最长公共子序列。
b.若xm≠yn,且zk≠xm,则Z是Xm-1和Y的最长公共子序列。
c.若xm≠yn,且zk≠yn,则Z是X和Yn-1的最长公共子序列。
其中,Xm-1={x1,x2,…,xm-1};Ym-1={y1,y2,…,yn-1};Zk-1={z1,z2,…,zk-1}。
② 子问题的递归结构
首先建立子问题最优值的递归关系。用c[i][j]记录序列Xi和Yj的最长公共子序列的长度。其中,X={x1,x2,…,xm};Y={y1,y2,…,yn}。当i=0或j=0时,空序列是Xi和Yj的最长公共子序列,故此时c[i][j]=0。在其他情况下,由最优子结构性质课件里递归关系如下:
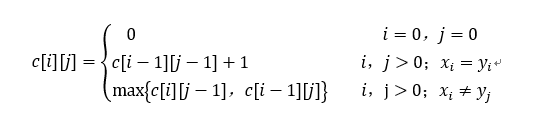
③计算最优值
以序列X和Y作为输入。输出两个数组c和b。其中c[i][j]存储Xi和Yj的最长公共子序列的长度,b[i][j]记录c[i][j]的值是由哪一个子问题的解得到的,这在构造最长公共子序列时要用到。问题的最优值,即X和Y的最长公共子序列的长度记录与c[m][n]中。
④构造最长公共子序列
首先从b[m][n]开始,依其值在数组b中搜索。当b[i][j]=1时,表示Xi和Yj的最长公共子序列是由Xi-1和Yj-1的最长公共子序列在尾部加上xi所得到的子序列;当b[i][j]=2时,表示Xi和Yj的最长公共子序列与Xi-1和Yj的最长公共子序列相同;当b[i][j]=3时,表示Xi和Yj的最长公共子序列与Xi和Yj-1的最长公共子序列相同。
时间复杂性分析:
a.计算最优值
由于每个数组单元的计算耗费O(1)的时间,此部分算法耗时为O(mn)。
b.构造最长公共子序列
该算法每一次递归调用使i或j减1,因此算法的计算时间为O(m+n)。
生成的数据可导入EXCEL中进行数据分析生成分析图表。


