C++分治策略实现线性时间选择
问题描述:
给定线性序集中n个元素和一个整数k,1≤k≤n,要求找出这n个元素中第k小的元素,即如果将这n个元素依其线性序排列时,排在第k个的元素即为要找到元素。
细节须知:(与之前的随笔相比)
(1)设置了对于程序运行次数的手动输入设定
(2)取消了文件的读入,直接生成随机数进行排序查找
(3)扩大了随机数的范围、数组的可申请大小
(4)时间统计精确到了微秒级
(5)运行结束后一次性写入提升了程序稳定性,写入的数据可用于数据分析图表
算法原理:
将n个输入元素划分成⌈n/5⌉个组,每组5个元素,只可能有一个组不是5个元素。用任意一种排序算法,将每组中的元素排好序,并取出每组的中位数,共⌈n/5⌉个。递归调用算法Select来找出⌈n/5⌉个元素的中位数。如果⌈n/5⌉是偶数,就找它的两个中位数中较大的一个。以这个元素作为划分基准。以此递归排序找到所需的第k项。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstdlib> 4 #include<cstring> 5 #include<fstream> 6 #include<algorithm> 7 #include<windows.h> 8 #include<ctime> 9 using namespace std; 10 LARGE_INTEGER nFreq;//LARGE_INTEGER在64位系统中是LONGLONG,在32位系统中是高低两个32位的LONG,在windows.h中通过预编译宏作定义 11 LARGE_INTEGER nBeginTime;//记录开始时的计数器的值 12 LARGE_INTEGER nEndTime;//记录停止时的计数器的值 13 14 //一次快排 15 int Partition(int nums[],int p,int r,int x) 16 { 17 if(p>r) return -1; 18 //找出基准x的位置并与第一位交换 19 for(int i=p;i<=r;i++) 20 { 21 if(nums[i]==x) 22 { 23 swap(x,nums[p]); 24 break; 25 } 26 } 27 int left=p,right=r; 28 while(left<right) 29 { 30 while(left<right && nums[right]>=x) right--; 31 nums[left]=nums[right]; 32 while(left<right && nums[left]<x) left++; 33 nums[right]=nums[left]; 34 } 35 nums[left]=x; 36 return left; 37 } 38 39 //快速排序 40 void QuickSort(int nums[],int low,int high) 41 { 42 if(low>high) return; 43 int key=nums[low]; 44 int left=low,right=high; 45 while(left<right) 46 { 47 while(left<right && nums[right]>=key) right--; 48 nums[left]=nums[right]; 49 while(left<right && nums[left]<key) left++; 50 nums[right]=nums[left]; 51 } 52 nums[left]=key; 53 QuickSort(nums,low,left-1); 54 QuickSort(nums,left+1,high); 55 } 56 57 int Select(int nums[],int p,int r,int k) 58 { 59 if(r-p<75) 60 { 61 QuickSort(nums,p,r); 62 return nums[p+k-1]; 63 } 64 //每5个为一组,找到各组的中位数,并存储在前(r-p-4)/5个位置里 65 for(int i=0;i<=(r-p-4)/5;i++) 66 { 67 QuickSort(nums,p+5*i,p+5*i+4); 68 swap(nums[p+i],nums[p+5*i+2]); 69 } 70 //找所有中位数的中位数 71 int x=Select(nums,p,p+(r-p-4)/5,(r-p-4)/10); 72 //以x为基准做一次快排 73 int i=Partition(nums,p,r,x); 74 int j=i-p+1; 75 //判断k属于那个部分 76 if(k<=j) 77 return Select(nums,p,i,k); 78 else 79 return Select(nums,i+1,r,k-j); 80 } 81 int main(){ 82 ofstream fout; 83 double cost; 84 int i = 0,m = 0,n = 0,key = 0; 85 cout<<"Please enter the number of times you want to run the program:"; //输入程序运行次数 86 cin>>m; 87 int data_amount[m]; 88 double runtime[m]; 89 srand((unsigned int)time(NULL)); //设置随机数种子 90 for(i=0;i<m;i++) 91 { 92 n=10000+RAND_MAX*(rand()%300)+rand(); //RAND_MAX=32767,随机生成数据量 93 data_amount[i]=n; //限定数据规模为10000~9872867 94 cout<<"☆The "<<i+1<<"th test Data amount is:"<<n<<endl; 95 int j=0; 96 int *a=(int *)malloc(n*sizeof(int)); 97 for(j=0;j<n;j++){ 98 a[j]=RAND_MAX*(rand()%400)+rand(); //随机生成0~13139567的随机数 99 } 100 key=rand()%10000+1; //随机生成1~10000作为所要选择的次序 101 QueryPerformanceFrequency(&nFreq);//获取系统时钟频率 102 QueryPerformanceCounter(&nBeginTime);//获取开始时刻计数值 103 int t=Select(a,0,n-1,key); 104 QueryPerformanceCounter(&nEndTime);//获取停止时刻计数值 105 cost=(double)(nEndTime.QuadPart - nBeginTime.QuadPart) / (double)nFreq.QuadPart; 106 runtime[i]=cost; 107 cout<<"The "<<key<<"th number is:"<<t<<endl; 108 cout<<"The running time is:"<<cost<<" s"<<endl; 109 free(a); 110 } 111 fout.open("data.txt"); 112 if(!fout){ 113 cerr<<"Can not open file 'data.txt' "<<endl; 114 return -1; 115 } 116 for(i=0;i<m;i++){ 117 fout<<data_amount[i]<<","<<runtime[i]<<endl; 118 } 119 fout.close(); 120 cout<<"Success!"<<endl; 121 return 0; 122 }
程序设计思路:
假设输入的数据规模为n,要查找的数据次序为k。
(1)判断数组长度,若小于75则直接进行快速排序,否则进行之后的算法。
(2)将n个输入元素划分成⌈n/5⌉个组,每组五个元素。用快速排序将每组中的元素排好序,并确定每组的中位数,共⌈n/5⌉个。
(3)递归调用算法Select来找出这⌈n/5⌉个元素的中位数。如果⌈n/5⌉是偶数,就找它的两个中位数中较大的一个。以这个元素作为划分基准。
(4)以此递归调用进行排序,最终搜索得到要找的第k项。
时间复杂性分析:
为了分析算法Select的计算时间复杂性,设n=r-p+1,即n为输入数组的长度。算法的递归调用只有在n≥75时才执行。因此,当n<75是算法Select所用的计算时间不超过一个常数C1。找到中位数的中位数x后,算法Select以x为划分基准调用Partition对数组a[p:r]进行划分,这需要O(n)时间。算法Select的for循环体行共执行n/5次,每一次需要O(1)时间。因此,执行for循环共需O(n)时间。
设对n个元素的数组调用算法Select需要T(n)时间,那么找中位数的中位数x至多用了T(n/5)的时间。已经证明了,按照算法所选的基准x进行划分所得到的2个子数组分别至多有3n/4个元素。所以,无论对哪一个子数组调用,Select都至多用了T(3n/4)的时间。
总之,可以得到关于T(n)的递归式
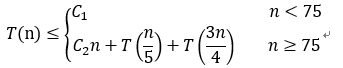
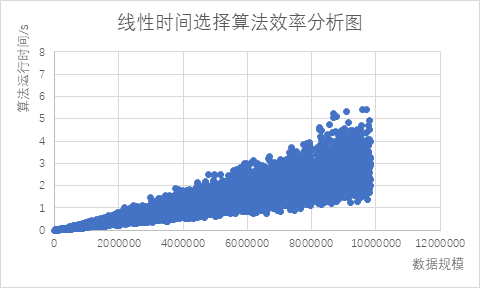
解此递归式可得T(n)=O(n)。
经过5000次不同规模数据的实验并统计运行时间得到如下算法效率分析图: